
例:求标量场= ln(x2++z2)通过点M(1,2,3)的等值面方程。解:函数在点M(1,2,3)处的值为Φ = ln(x? + y2 +z2) = ln(1? +22 +33) = ln 14故通过点M(1,2,3)的等值面方程In(x2 + y2 +z2)= ln 14即x? + j? +2?=14
例:求标量场 通过 点M(1,2,3)的等值面方程。 ln( ) 2 2 2 = x + y + z 解:函数在点M(1,2,3)处的值为 ln( ) ln(1 2 3 ) ln14 2 2 2 2 2 2 = x + y + z = + + = 故通过点M(1,2,3)的等值面方程 ln( ) ln14 2 2 2 x + y + z = 14 2 2 2 即 x + y + z =
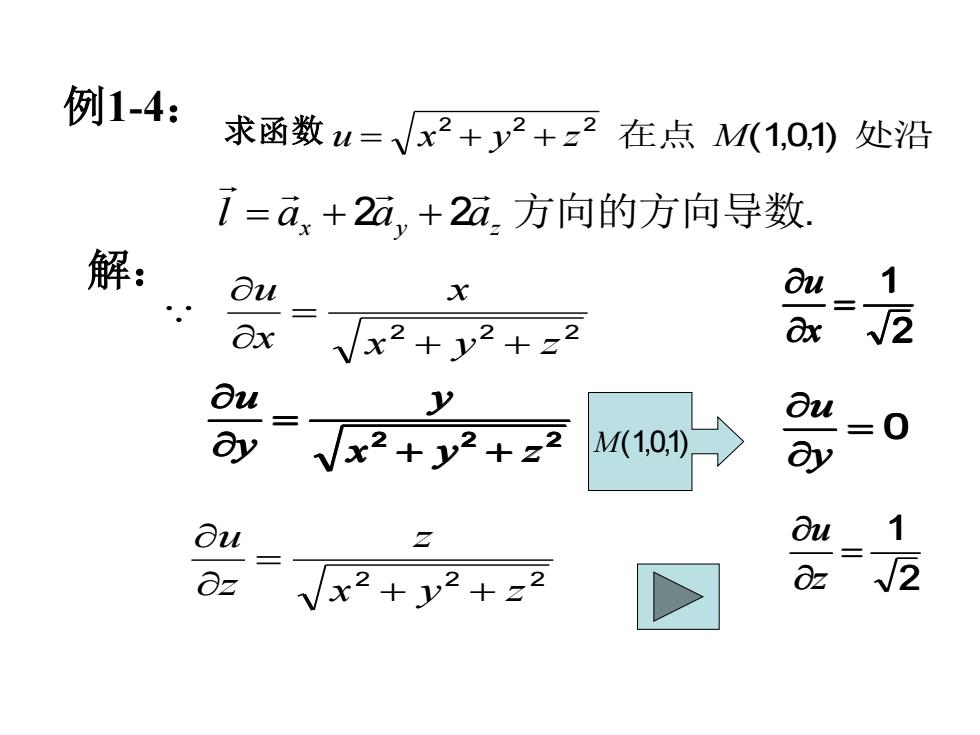
例1-4:求函数u=/x2+2+z2 在点 M(1,0,1)处沿7=a,+2a,+2a方向的方向导数解:au1Oux2axax+2+z2auyu=0M(1,0,1)ayVay1ouauZ-2OzOz
例1-4: 求函数 u = x 2 + y 2 + z 2 在点 M(1,0,1) 处沿 l a 2a 2a 方向的方向导数. x y z = + + 解: 2 2 2 x y z x x u + + = 2 2 2 x y z y y u + + = 2 2 2 x y z z z u + + = M(1,0,1) 2 1 = x u = 0 y u 2 1 = z u 2 2 2 x y z y y u + + = 2 1 = x u = 0 y u 2 2 2 x y z y y u + + = 2 1 = x u 2 1 = z u = 0 y u 2 2 2 x y z y y u + + = 2 1 = x u

=a+27-2a而7的方向余弦为Al =aAx+a,Ay+a.Az11COSX32VP+2+2cosB3V12+ 22+ 2222cOS:3/12 + 22 + 22函数u在M点沿7方向的方向导数为:211121Ou+0xV223323al
而 l 的方向余弦为 3 1 1 2 2 1 cos 2 2 2 = + + = 3 2 1 2 2 2 cos 2 2 2 = + + = 3 2 1 2 2 2 cos 2 2 2 = + + = 2 1 3 2 2 1 3 2 0 3 1 2 1 = + + = l M u 点沿 l 方向的方向导数为: 函数 u 在 M ax ay az l = + 2 + 2 l a x a y a z = x + y + z 3 1 1 2 2 1 cos 2 2 2 = + + = 3 2 1 2 2 2 cos 2 2 2 = + + =

例: 求标量场 u= xy2 +yz3 在点M(2,-1,1)处的梯度,以及在矢量i=2a,+2a,-a.方向的方向导数解:OuOuOugradiOzOxOya,y? +a,(2xy+z3) +a,3yz2M(2,-1,1)VuM=ax-3a,-3a而7的方向余弦为
例: 求标量场 u = x y 2 + yz 3 在点 M(2,−1,1)处 的梯度,以及在矢量 l 2 a 2 a a 方向的方向导数. x y z = + − 解: zu a yu a xu gradu a x y z + + = 2 3 2 a y a ( 2x y z ) a 3yz x y z = + + + M ( 2 , − 1 , 1 ) M x y z u a a a = − 3 − 3 而 l 的方向余弦为

I = 2a +2a,-a.2-2cosα =3/22 +22 +(-1)222cosB=3/22 +22 +(-1)21--1cOSy3V22 +2? +(-1)2函数u在M点沿1方向的方向导数为2Ou27=1x-3)al lm33
3 2 2 2 ( 1) 2 cos 2 2 2 = + + − = 3 2 2 2 ( 1) 2 cos 2 2 2 = + + − = 3 1 2 2 ( 1) 1 cos 2 2 2 = − + + − − = 点沿 l 方向的方向导数为: 函数 u 在 M 3 1 ) 3 1 ( 3) ( 3 2 ( 3) 3 2 =1 + − + − − = − l M u l 2a 2a a . x y z = + −