《电磁场与电磁能》课程PPT教学课件（马冰然版）总结复习

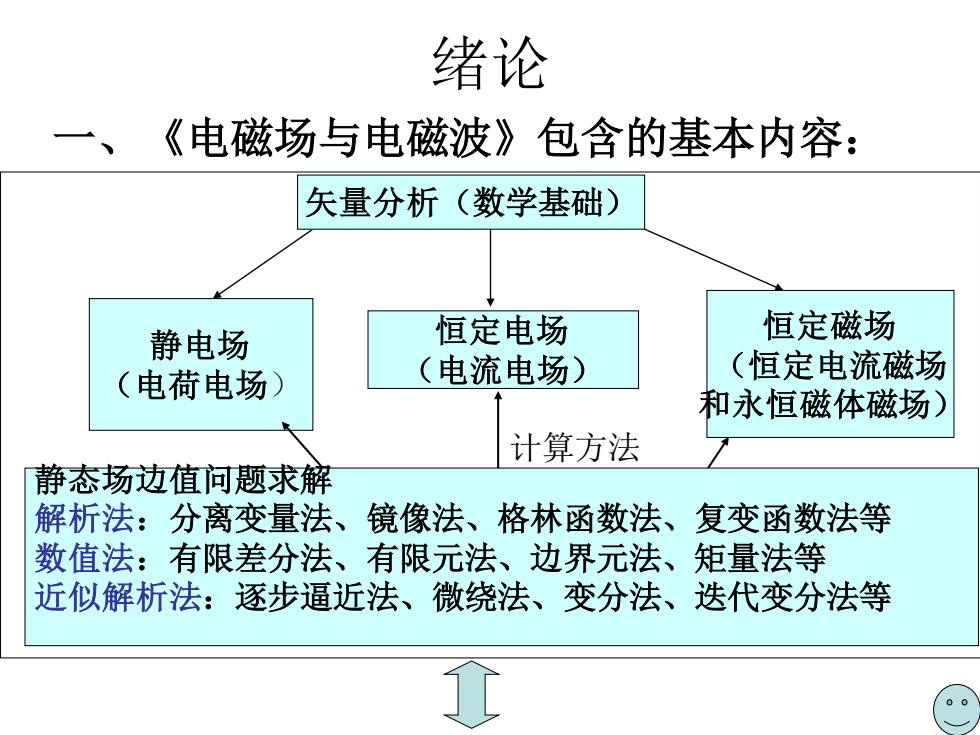
绪论《电磁场与电磁波》包含的基本内容：矢量分析（数学基础）恒定磁场恒定电场静电场（恒定电流磁场（电流电场）（电荷电场）和永恒磁体磁场）计算方法静态场边值问题求解解析法：分离变量法、镜像法、格林函数法、复变函数法等数值法：有限差分法、有限元法、边界元法、矩量法等近似解析法：逐步逼近法、微绕法、变分法、迭代变分法等↑

计算方法 绪论 一、《电磁场与电磁波》包含的基本内容： 静电场 （电荷电场） 恒定电场 （电流电场） 恒定磁场 （恒定电流磁场 和永恒磁体磁场） 矢量分析（数学基础） 静态场边值问题求解 解析法：分离变量法、镜像法、格林函数法、复变函数法等 数值法：有限差分法、有限元法、边界元法、矩量法等 近似解析法：逐步逼近法、微绕法、变分法、迭代变分法等

麦克斯韦位移电流假说法拉第电磁感应定律基础（变化电场产生磁场）（变化磁场产生电场）基础基础总结总结总结标量位函数时变场高斯定理完整的Maxswell方程组矢量位函数磁通连续性定理边界条件基础应用总结总结基础实例均匀平面波的传播电磁波的辐射波导和谐振腔微波元件微波电路

完整的Ｍaxswell方程组 法拉第电磁感应定律 （变化磁场产生电场） 麦克斯韦位移电流假说 基础 （变化电场产生磁场） 基础 总结 总结 基础 总结 时变场高斯定理 磁通连续性定理 标量位函数 矢量位函数 边界条件 基础 总结 应用 总结 基础 实例 均匀平面波的传播 电磁波的辐射 波导和谐振腔 微波元件 微波电路

第一章矢量分析与场论基础

第一章 矢量分析 与场论基础

一、场标量场量场静态场时变场A-AA-aA +a,A, +a.A.aM="A矢量球柱坐标 dl, =drdlr =drdl。= rdedl。= rdp长度元dl。= rsinadpdl, =dz面积元为：dS, = dl, dl, = rd pdz( ds, = dledl。 = r? sinodedpdS, = dydzdS.= dl.dl. = drdzdS。 = dl,dl,=r sinodrdpdS, = dxdz dS。= dl,dl。=rdrdoI dS, = dl,dl, = rdrdpdS, = dxdy体积元aV = dxdydzdV = dl, dl dl, = r? sin &drdedpdV = dl,dl,dl, = rdrd pdz

一、场 标量场 矢量场 静态场 时变场 A A A A A a = = 面积元为： dS dxdy z = dS dydz x = dS dxdz y = 体积元 dV = dxdydz dS dl dl rd dz r =  z =  dS dl dl drdz r z = =  dSz = dlr dl = rdrd dV dl dl dl rdrd dz = r  z =  dS = dlr dl = rdrd dSr dl dl r sindd 2 = = dS = dlr dl = r sindrd dV dlr dl dl r sin drdd 2 = = dl = r sind dl dr r = dl = rd 球 dl dz z = dl dr r = dl = rd 柱坐标 长度元 A ax Ax ay Ay az Az     矢量 = + +

二、矢量运算1.矢量加法和减法：A+B=a(A +B,)+a(A, +B,)+a(A, +B.)A·B=|A|Bcos(A,B)2.点积（或标量积）A-B=AxBx+AyBy+Az Bz3.又积（或矢量积）AxB=ABsin(A,B)axayaAxB=AMAyBxB,B=(A,B: -A,B,)ax+(A,Bx-A,B.)ay +(A,B,-A,Bx)a

1.矢量加法和减法： ( ) ( ) ( ) x x x y y y z Az Bz A+ B = a A + B + a A + B + a +      2.点积（或标量积） AB = A B cos(A,B) A·B=AxBx+AyBy+AzBz 3.叉积（或矢量积） AB = A B sin(A,B) y z z y x z x x z y x y y x z x y z x y z x y z A B A B a A B A B a A B A B a B B B A A A a a a ( ) ( ) ( ) = − + − + − AB = 二、矢量运算