西安交通大学：《电磁场与电磁能》课程教学资源（PPT课件）第四章 时变电磁场

AKD4.1.3全电流定律恒定场时变场aDop.: V.J::V.J=0atataD V-(J+=0at矢量恒等式矢量恒等式V-(VxH)= 0V-(VxH)=0ad..VXH=J.. VxH=J-at图4.1.4交变电路用安培环路定律面积分，斯氏定理面积分，斯氏定理aD作闭合曲线1与导线交fH.dl- J,-dsSH·dl=).dsat链，根据安培环路定律经过S,面经过S,面SH-dl =$ H.dl =J.ds=0J·ds=iJ.ds=iaDfHdl=J(J+厨思考).dsaDatods-gds-1为什么相同的线积分结果不同？S2atJS2atat

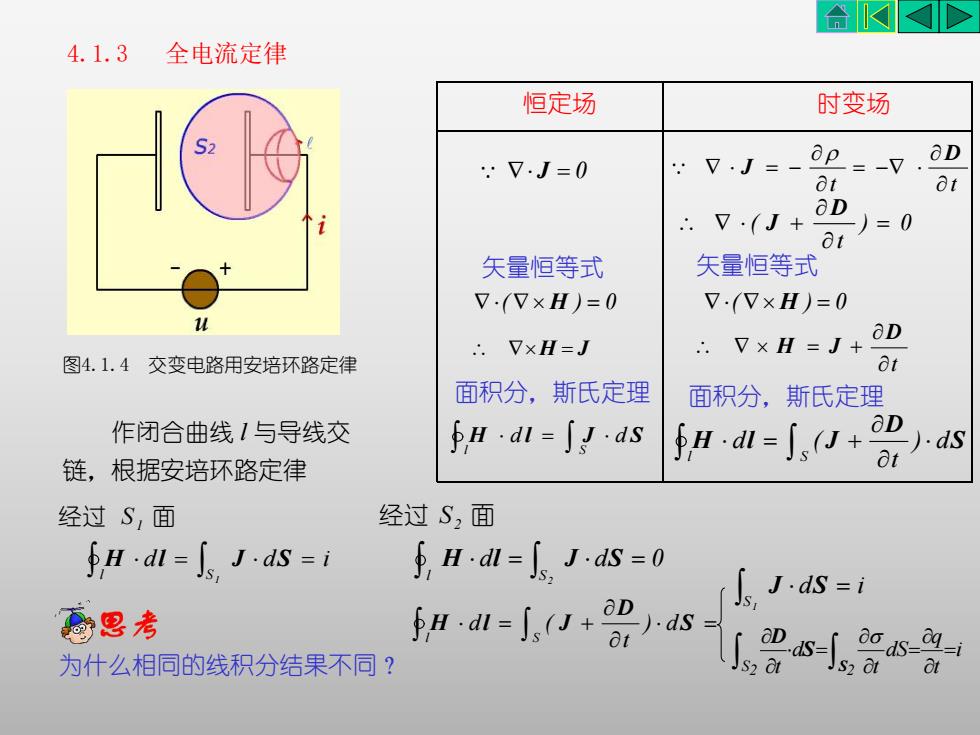
作闭合曲线 l 与导线交 链，根据安培环路定律 d d i S 1 l S 1       H l J S 经过 面 d d 0 S S2 l 2       H l J S 经过 面          S D H l J ) d t d ( l S            S2 2 i t q dS t d t S S D  d i S1    J S 4.1.3 全电流定律 恒定场 时变场   J  0  (   H )  0  H  J t       D H J 面积分，斯氏定理      l S H d l J d S S D H l J ) d t d ( l S         面积分，斯氏定理  (  H )  0 t  t           D J   ) 0 t (        D J 矢量恒等式 矢量恒等式 图4.1.4 交变电路用安培环路定律 为什么相同的线积分结果不同？

合A#全电流定律aDVXH=J+微分形式ataDfH.dl-(J+2).ds=i,+ip积分形式ataD=JD其中，at位移电流密度(DisplacementCurrentDensity )全电流定律揭示不仅传导电流激发磁场，变化的电场也可以激发磁场。它与变化的磁场激发电场形成自然界的一个对偶关系。麦克斯韦由此预言电磁波的。例4.1.1已知平板电容器的面积为S，相距为d，介质的介电常数8发极板间电压为u（t）。试求位移电流ip:传导电流i与ip的关系是什么？解：忽略极板的边缘效应和感应电场E=uD=6E=eu(t)电场d'daD_du位移电流密度Jp=atddt传导电流(du)=cduip=Jpds-位移电流+位移电流=icddtdt图4.1.5传导电流与位移电流

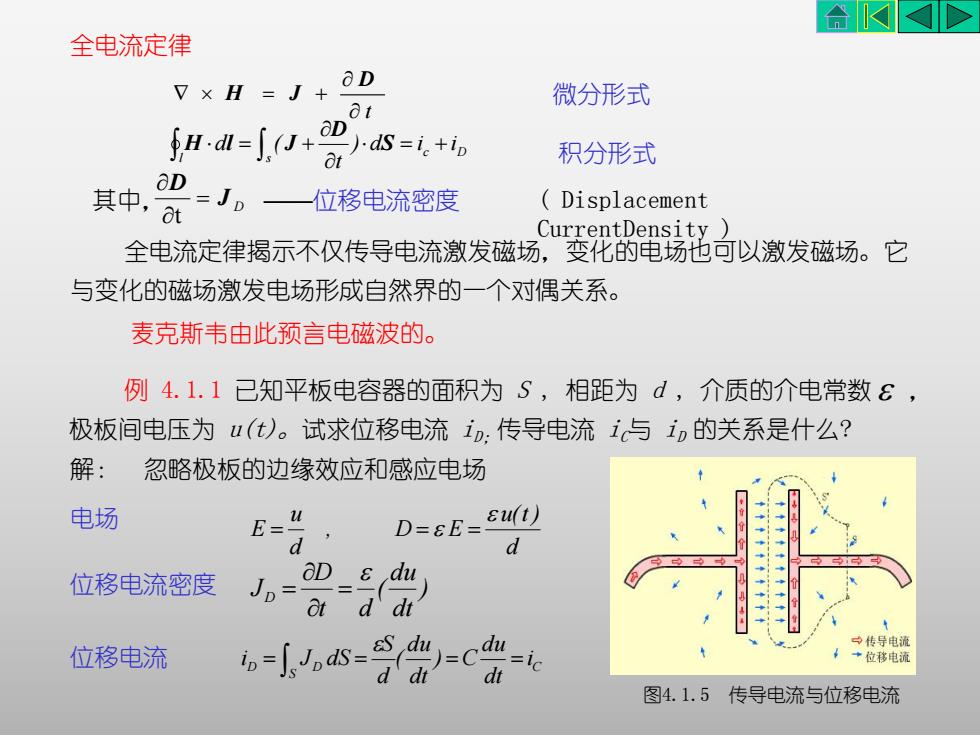
全电流定律 全电流定律揭示不仅传导电流激发磁场，变化的电场也可以激发磁场。它 与变化的磁场激发电场形成自然界的一个对偶关系。 麦克斯韦由此预言电磁波的。 其中， J D ——位移电流密度 D    t ( Displacement CurrentDensity ) 解： 忽略极板的边缘效应和感应电场 d u(t ) , D E d u E      位移电流密度 位移电流 ) dt du ( t d D JD      C S D D i dt du ) C dt du ( d S i  J dS      例 4.1.1 已知平板电容器的面积为 S , 相距为 d , 介质的介电常数 ， 极板间电压为 u(t)。试求位移电流 iD；传导电流 iC与 iD 的关系是什么?  电场  t      D H J 微分形式 c D l s ) d i i t d (           S D H l J 积分形式 图4.1.5 传导电流与位移电流

AD4. 2电磁场基本方程组·分界面上的衔接条件4.2.1电磁场基本方程组综上所述，电磁场基本方程组（Maxwel1方程）为ODaDfH.dl=L(J+VXH=J+).ds全电流定律atataBaBfE - dl = -I.%f.dsVXE=电磁感应定律at$B-ds = 0V·B=0磁通连续性原理JsV.D=pf Dds = q高斯定律2讨论与引伸四个方程所反映的物理意义全电流定律麦克斯韦第一方程，表明传导电流和变化的电场都能产生磁场：·电磁感应定律麦克斯韦第二方程，表明电荷和变化的磁场都能产生电场；·磁通连续性原理一一表明磁场是无源场，磁力线总是闭合曲线；·高斯定律一一表明电荷以发散的方式产生电场（变化的磁场以涡旋的形式产生电场）。·麦克斯韦第一、二方程是独立方程，后面两个方程可以从中推得。静态场和恒定场是时变场的两种特殊形式

4.2 电磁场基本方程组 • 分界面上的衔接条件 4.2.1 电磁场基本方程组 综上所述,电磁场基本方程组 (Maxwell方程)为 S D H l J D H J ) d t d ( t l s               S B E l B E d t d t l k               0 d 0 s       B B S       s D  D dS q 全电流定律 电磁感应定律 磁通连续性原理 • 全电流定律——麦克斯韦第一方程, 表明传导电流和变化的电场都能产生磁场； • 电磁感应定律——麦克斯韦第二方程 , 表明电荷和变化的磁场都能产生电场； • 磁通连续性原理——表明磁场是无源场,磁力线总是闭合曲线； • 高斯定律——表明电荷以发散的方式产生电场(变化的磁场以涡旋的形式产生电场)。 • 麦克斯韦第一、二方程是独立方程，后面两个方程可以从中推得。 • 静态场和恒定场是时变场的两种特殊形式。 高斯定律 四个方程所反映的物理意义

AKV4. 2. 2分界面上的衔接条件时变电磁场中媒质分界面上的衔接条件的推导方式与前三章类同，归纳如下：tan α-磁场：Bin=B2mtan α2μ2H-Hu= k折射定律tan β= i电场：D2n-Din=αtan β,62E, = E例4.2.1试推时变场中导理想导体与理想介质分界面上的衔接条件。y-0解：：理想导体中 J=E为有限值，当→0,E=0;aB+H: VxE=-=0B=C(常数),KataB若C0,B由0→C的建立过程中必有￥0.即E±0EnatOJ=E→80，所以,只有B=C=0。图4.2.1媒质分界面为此：·在理想导体内部没有电磁场，即E=0，B=0；·分界面介质侧的衔接条件为E,=0,D,=o,H=k,B,=0电磁波的全反射

时变电磁场中媒质分界面上的衔接条件的推导方式与前三章类同，归纳如下： 例 4.2.1 试推时变场中导理想导体与理想介质分界面上 的衔接条件。 0 , C ( ), t    常数      B B  E 4.2.2 分界面上的衔接条件 所以 只有 若 由 的建立过程中必有 即 , , 0, 0 t 0, 0          J E E B C B C   B  C  0 解： 理想导体中 J  E 为有限值，当   , E  0 ; E2t  E1t 电场： D2n D1n  H H k 2t  1t  磁场：B1n  B2n 为此： • 在理想导体内部没有电磁场，即 E=0，B=0 ； 折射定律 2 1 2 1 tan tan      2 1 2 1 tan tan      图4.2.1 媒质分界面 Et 0, Dn  , Ht  k, Bn 0 • 分界面介质侧的衔接条件为 电磁波的全反射

AKD4.3动态位及其积分解动态位及其微分方程4.3.1仍从电磁场基本方程组出发，由V.B=0B=VXA1aBaAA由IVxE=Vx(EE+-Vo0>atatatA, @ofKineticState)。称为动态位（potentialaDaOA1由VxH=J+-Vo)VxVXA=J-atatatLOA由V.D=po)=pV.E(→atO"Aap经整理后，得A-(1)J+(VA+et?ataPV.A=-Vp+(2)Ot8ap定义A的散度洛仑兹条件（规范）V.A=-eat

4.3 动态位及其积分解 4.3.1 动态位及其微分方程 仍从电磁场基本方程组出发, 由   B  0  t     B 由 E         ) 0 t ( A E      t A E t     D H J ) t ( t 1               A A J  D              ) t ( A 经整理后，得  A,  称为动态位（potential of Kinetic State）。 由 由 t ( ) t 2 2 2                 J A  A A           A t 2 （2） （1） 洛仑兹条件（规范） t      A  B A 定义A 的散度