西安交通大学：《电磁场与电磁能》课程教学资源（PPT课件）第七章 均匀传输导线中的导行电磁波

第7章均匀传输线中的导行电磁波 7.0序 7.1无损耗均匀传输线方程 7.2无损耗均匀传输线的传播特性 7.3无损耗传输线中波的反射和透射 7.4无损耗传输线的入端阻抗 7.5无损耗均匀传输线的阻抗匹配 7.6有损耗均匀传输线

第 7 章 均匀传输线中的导行电磁波

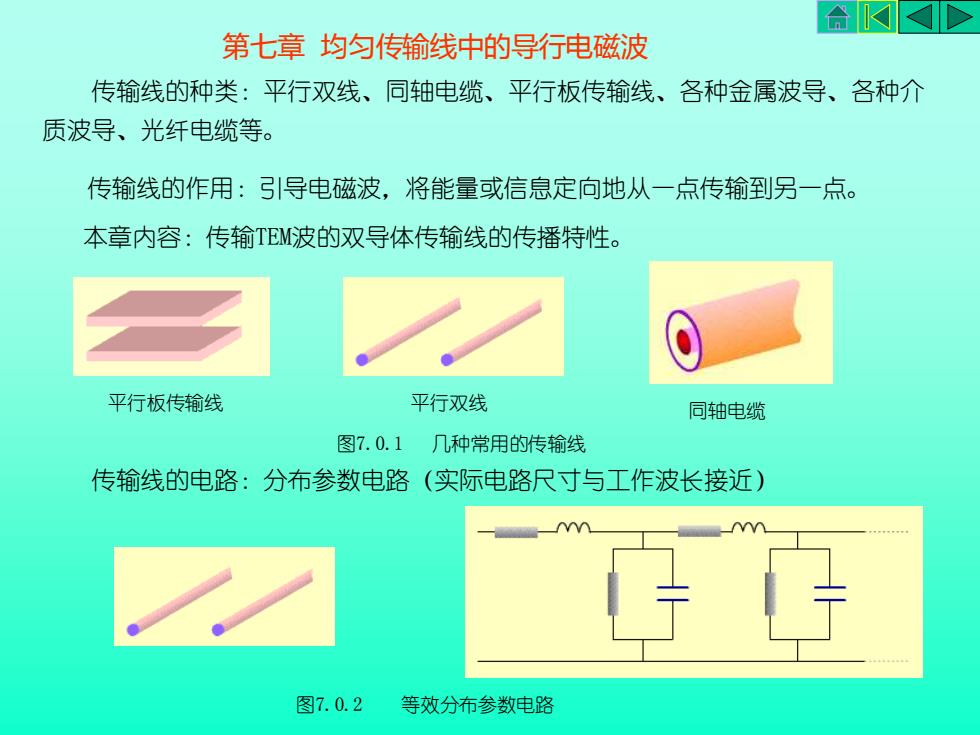
AKKD第七章均匀传输线中的导行电磁波传输线的种类：平行双线、同轴电缆、平行板传输线、各种金属波导、各种介质波导、光纤电缆等。传输线的作用：引导电磁波，将能量或信息定向地从一点传输到另一点。本章内容：传输TEM波的双导体传输线的传播特性。平行板传输线平行双线同轴电缆图7.0.1几种常用的传输线传输线的电路：分布参数电路（实际电路尺寸与工作波长接近）VV图7.0.2等效分布参数电路

第七章 均匀传输线中的导行电磁波 传输线的种类：平行双线、同轴电缆、平行板传输线、各种金属波导、各种介 质波导、光纤电缆等。 传输线的作用：引导电磁波，将能量或信息定向地从一点传输到另一点。 本章内容：传输TEM波的双导体传输线的传播特性。 平行板传输线 平行双线 同轴电缆 图7.0.1 几种常用的传输线 传输线的电路：分布参数电路（实际电路尺寸与工作波长接近） 图7.0.2 等效分布参数电路

合KD7.1无损耗均匀传输线方程假设传输线均匀且无损耗，传播TEM波。Zi=0结点电流方程aidzi +LodzazaiaaOudz)dz+C,dzi=i+(u+azatOz(z,t)+Xaudz.....Codzu(z,t)u+az回路电压方程Zu=0aiauu= Ldzdz+u+图7.1.1均匀传输线电路模型atOz同除以dz，略去二阶无穷小项（dz）2，得传输线方程i+couu+L.oOFLOtoatO-进一步整理。得电压u，电流i的波动方程a'i-lai'uoulou=LC.0%=LC.OCavarwatO2"at1式中v传播速度，L、C。分别为传输线单位长度的电感及电容二VL.C

7.1 无损耗均匀传输线方程 假设传输线均匀且无损耗，传播TEM波。 结点电流方程 i = 0 dz) z u ( u t dz C dz z i i i 0   +   +   = + 回路电压方程 u = 0 dz z u u t i u L dz 0   + +   = 同除以dz，略去二阶无穷小项（dz) 2，得传输线方程 0 t u C z i 0 =   +   0 t i L z u 0 =   +   图7.1.1 均匀传输线电路模型 进一步整理。得电压u，电流 i 的波动方程 2 2 2 2 2 2 0 0 2 t u v 1 t u L C z u   =   =   2 2 2 2 2 2 0 0 2 t i v 1 t i L C z i   =   =   式中 —— 传播速度, 分别为传输线单位长度的电感及电容 L0C0 1 v = L0、C0

ANKD7.2无损耗均匀传输线的传播特性7.2.1瞬态解a'u'uu(zt)=u(t-三)+u(t+二)波动方程=L,C,波动方程的解ata22oiaii(2,t)=t(t-三)+t(t+三)=L.CoarO1分别称为入射电压波、电流波：反射电压波、电流波。7.2.2正弦稳态解dd'u=(jo)LCU=ku=(jo)LCi=kidz?dz?式中k=iB=jo/Lc相位常数传播常数：β=OVLC方程的解U(=)=te-i+U-ea1i(z)=ite-准+ie-作=（Ue-i-U-e）Z.式中Zo特性阻抗U+U-Lo2Z. =（实数）itiVC

7.2 无损耗均匀传输线的传播特性 7.2.1 瞬态解 波动方程的解 ) v z ) u (t v z u( z,t ) = u (t − + + + − ) v z ) i (t v z i( z,t ) = i (t − + + + − 分别称为入射电压波、电流波；反射电压波、电流波。 7.2.2 正弦稳态解 ( j ) L C I k I dz d I ( j ) L C U k U , dz d U 2 0 0 2 2 2 2 0 0 2 2 2       =  = =  = 式中 k = j = j L0C0 ——传播常数；  = L0C0 ——相位常数 方程的解 j z j z U( z ) U e U e + −  −   =  +  (U e U e ) Z 1 I( z) I e I e j z j z 0 + − jz − − jz + −  −   =  +  =  −  式中 Z0 ——特性阻抗 = = − − =  − + + 0 0 0 C L I U I U Z     （实数） 波动方程 2 2 2 0 0 2 t u L C z u   =   2 2 2 0 0 2 t i L C z i   =  

AKKD1. 已知始端电压 亡,和电流I,(z=-l)将已知条件代入通解i+0=i+U-iUU,Z11-(-0")a解得复常数为ozUt=-(u,+zie-inU-=,(U,-Z,i,Jejm图7.2.1已知ui的传输线2代入通解，得U(2)=(U,+Z,1, )e-8(42) +号(U,-Z.i,Je(z)++i,Je-p(+2) -iJeB(I+z)i(=)=一利用欧拉公式，得U(=)=U,cos β(l+z)-jZ,i, sinβ(l+=)i(=)=i,cos β(1+=)-jsinB(l+=)Z.z<0, 1>0注意：

1. 已知始端电压 U  1 和电流 I ( z l )  1 = − 将已知条件代入通解 j l j l U1 U e U +  −   =  +  (U e U e ) Z 1 I j l j l 0 1 +  − −   =  −  解得复常数为 j l 1 0 1 (U Z I )e 2 1 U + −   =  +  j l 1 0 1 (U Z I )e 2 1 U     = − − 利用欧拉公式，得 U(z) U cos (l z) jZ I sin (l z)  =  1  + − 0  1  + sin (l z ) Z U I( z ) I cos (l z ) j 0 1 = 1  + −  +    注意： z  0 , l  0 代入通解，得 j ( l Z ) 1 0 1 j ( l Z ) 1 0 1 (U Z I )e 2 1 (U Z I )e 2 1 U( z ) − + + = + + −        j ( l Z ) 1 0 j ( l Z ) 1 1 0 1 I )e Z U ( 2 1 I )e Z U ( 2 1 I( z ) − + + = + − −        图7.2.1 已知 U  1 ,I  1 的传输线