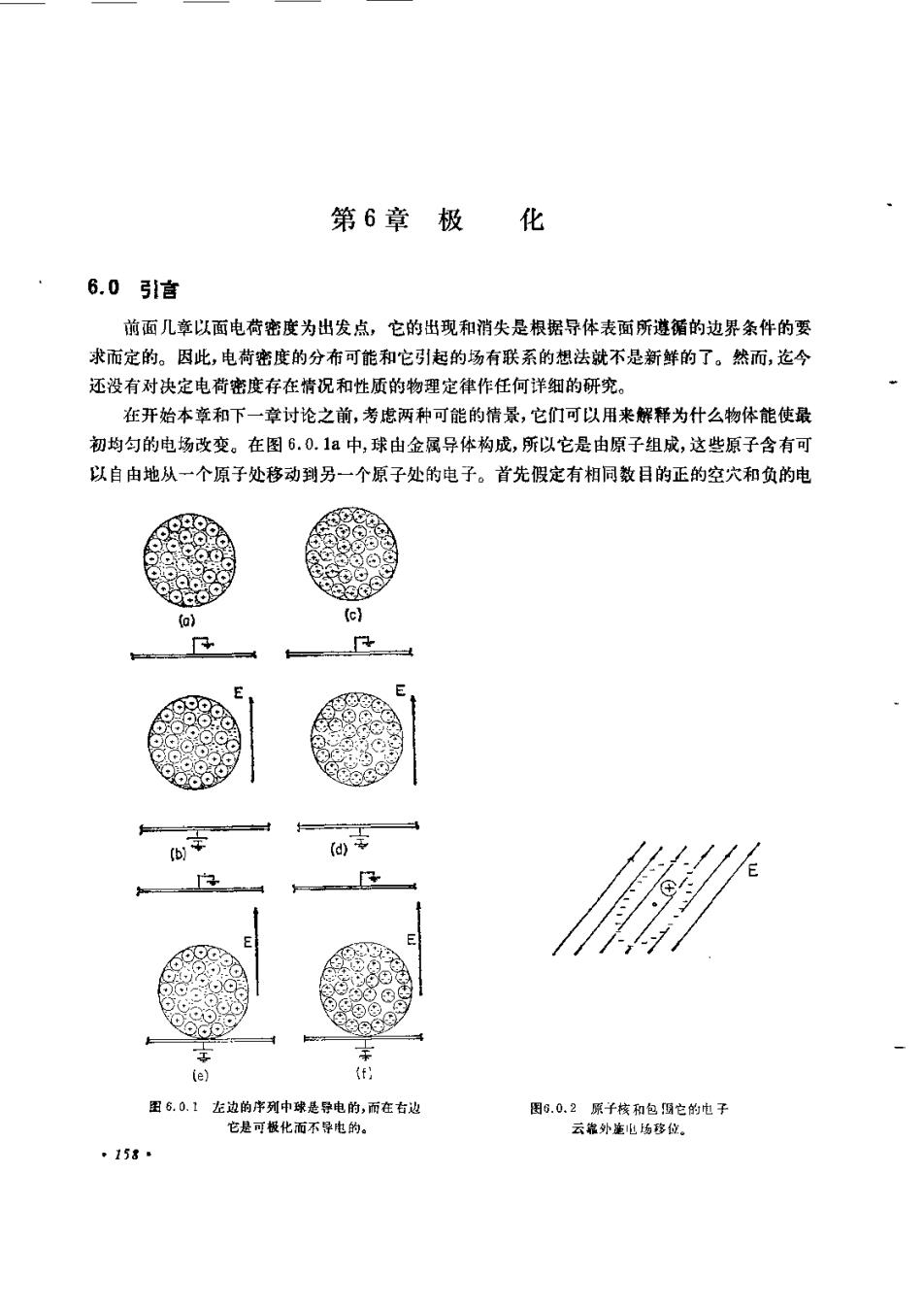
化第6章极6.0引言前面几章以面电荷密度为出发点,它的出现和消失是根据导体表面所遵循的边界条件的要求而定的。因此,电荷密度的分布可能和它引起的场有联系的想法就不是新鲜的了。然而,迄今还没有对决定电荷密度存在情况和性质的物理定律作任何详细的研究。在开始本章和下一章讨论之前,考虑两种可能的情景,它们可以用来解释为什么物体能使最初均勾的电场改变。在图6.0.1a中,球由金属导体构成,所以它是由原子组成,这些原子含有可以自由地从一个原子处移动到另一个原子处的电子。首先假定有相同数目的正的空穴和负的电(c)b图6.0.1左边的序列中球是导电的,而在右边图6.0.2原核和包俩它的电子居可极化面不街白云靠外施电场移位。158

子。在没在外加场以及在尺度比原子川的距离为大(即在宏观尺度)的情况下,在物质内部任一点都没有电荷密度。当这个物体放入原先均勾的电场中时,电子受到力的作用,此力企图使它们集中到球的南极。这只要求电子稍微向下移动(平均说来,小于原子间的距离)。因为在最终的平衡(稳定)状态,球的内部必须没有电场,所以在材料体积内各点电荷密度保持为零。但是,要维持净电荷为零,球北极原子正的位置是暴露的。过了一些时间,净结果是示于图 6.0.1b的面电荷密度分布。[事实上,如果电极远离球体,这就是例5.9.1中求得的分布。1现在考虑另一种物理情景,它能导致非常相似的结果。如图6.0.1c所示,材料由原子、分子或分子团(电畴)组成,在材料中电场感生偶极矩。例如,假设偶极短有原子的尺度,并且在没有电场时它不存在;偶极矩被感生是因为原子包含带正电的原子核以及沿着轨道绕原子核旋转的电子。按照量子理论,沿轨道绕原子核旋转的电子在任何特定瞬间不能看成是固定的。把电子设想成包围原子核的电荷“云"更为合适。由于沿轨道旋转的电子的电荷与原子核的电荷等量异号,中性的原子没有净电荷。不具有永久偶极矩的原子还有另外的性质,它的电子"云"的负电荷的中心与原子核的正电荷的中心重合。存在电场的情况下,正电荷的中心被拉向场的方向,而负电荷的中心被推向相反的方向。在原子范围,这一电荷中心的相对位移如图 6.0.2中所示。由于两个电荷的中心不再重合,粒子获得偶极矩。这样,我们可以用一对量值相等、符号相反,间距为&的电荷表示每个原子。在外施场内,在球体的宏观尺度上,出现偶极子,有点象图6.0.1d所示。在球的内部,极化使每个正电荷留在负电荷的附近,从而没有净电荷密度。但是在北极没有负电荷去中和正电荷,并且在南极没有正电荷与负电荷配对。结果就有面电荷密度分布,性质上与金属球情况下的结果没有差别。我们怎样能够区别这两种非常不同的情况:假设这两个球体都与下电极接触,如图中的(e)和(1)所示。这样做,我们的意思是在金属球的情况下,电子可自由地通过球与电极之间。电子仍旧是稍微向下移动,留下正的位置暴露在球的顶部。然而,有一些在底部的电子流入下电极,从而减少了在金属球下方负的面电荷的数量。在顶部,图6.0.1f 所示的极化了的球有类似的正的面电荷密度分布。但是这两种情况有一非常重要的差别是显而易见的。在理想电介质内,在原子尺度上沿轨道的电子与原来的原子是成对的,所以球一定保持中性。这样,金属球现在带有净电荷,而由偶极子组成的球没有净电荷。实验证明金属球确实获得了净电荷,它可以用一些不同的方法得到。其中两个从第1章的演示清楚地显示出来。对球体各通过“感应”的方式带电,将会相互推斥,这可由图1.3.10的实验显示。电荷也能根据电荷守恒进行测量,如演示1.5.1中那样。推测起来,用绝缘球进行同样的实验能够表明不存在净电荷。因为电荷的积聚是通过成对电荷的位移(极化)以及通过能够远离有相反符号的配对电荷的位移发生的,因此用把总电荷密度p分成p。和p,两部分,来区分这两部分电荷往往是合适的,Pu和P,分别由不成对的和成对的电荷产生。.159

(1)=pa+pp本章中考虑绝缘材料,所以集中注意成对的或极化电荷密度的作用。不成对电荷的额外的作用在下章中讨论。在6.1节中,我们第一步是建立极化电荷密度与偶极子强度一一极化强度*的关系。我们这样做是因为极化强度很容易确定。然后在 6.2和6.3两节注意两个一般的极化种类中的第一类。在这几节中,极化强度是永久的,所以确定时不考虑电场。在6.4节我们讨论表示场对极化的作用的简单构成定律。这种刚描述的由场感生的原子极化,是典型的物理情况。场对原子、分子或电畴的作用伴随有偶极子对场的反作用,必须同时考虑。即置于电场中的这种可极化物体的内部,产生极化电荷密度,反过来,它又改变了电场。在6.5—6.7诸节我们将学习一些方法,通过它们来获得这种问题的自相一致的解答。6.1极化强度下面的推导过程适用于具有各种微观起源的极化现象。无论代表的是原子、分子、有序的原子或分子团(电畴),或者甚至是宏观粒子、偶极子被描绘成相反的两个电荷士用矢量距离d分开,其方向从负电倚到正电荷。因此,单个偶极子,如4.4节所表示的,它的偶极矩P定义为p=qd(l)因为d的量值一般小于原子、分子或其他粒子的尺寸,所以它比所关心的任何宏观尺寸为小。现在考虑媒质由每单位体积N个这种极化粒子组成。在由面S包围的任意体积V内包含的净电荷是多少?显然,如果在V内媒质的粒子是未极化的,在V内的净电荷就是零。但是,现在它们是极化的,有些电荷在未极化状态时,中心包含在V内,现在移到面S的外面,而在里面留下未中和的电荷中心。要确定留在√内的净的未中和电荷,我们假设(不失一般性)在极化过程中电荷的负中心是不动的,只有电荷的正中心是可移动的。考虑图6.1.1所示在面S上面元da附近的d粒子。现在在S外面,体积de=d·da内的全部美推王的电荷正中心,都留下了负电荷中心。这些对V提供了净的负电荷。由于在dp内存在Nd·da个这种负电荷中心,留在V内的净电荷为(2)1Q=-f(aNd).da图6.1.1 含有正电荷的体积元,它将负电荷留在面8的另一边。E注意被积函数可以是正的或负的,取决于通过面元dα 的电荷的正中心是离开√还是进人V出现哪一种可能性与d和da的相对取向有关。如果d有一分量与da方向相同(机反),则电荷的正中心通过dα离开(进人)V。式(2)的被积函数具有每单位休积偶极矩的量纲,因此被定义为极化强度:原文为极化密度,本书按我国的习惯译虑极化强度。后网。评者许。.160

(3)P=Nqd此外还根据定义,V内的净电荷可以由极化电荷密度对它的体积积分确定Q=f,pdo(4)这样,我们有两种计算净电荷的方法,第一种方法是在式(2)的面积分中利用式(3)的极化强度。-f v.Pdu(5)Q--$p.da--这里已利用高斯定理将面积分转换成对被包照体积的体积分。从这个体积分求得的电荷、定与第二种计算净电荷的方法,即用(4)式求得的结果相同。由于所考虑的体积是任意的,在式(4)和(5)的体积分中的被积函数一定相同。(6)p,=-v-P这样,极化电荷密度P,就与极化强度P相关。在此推导过程中似乎没有达到目的,因为代替未知量Pp,出现了新的未知显P。在有些情况下,P是已知的。但是即使在较为常见的情况下,极化强度从而极化电荷密度事先是未知的,而是由场感生的,把P与E直接联系起来比使p,与E联系要更容易些在图6.0.1中,极化球得不到净电荷。我们用极化强度表示极化电荷密度就保证这是正确的。要明白这点,假设√被理解为包含整个极化体的体积,使包围体积V的面S落在极化体的外面。因为在 S上的P为零,式(5)的面积分一定为零。通过式(6)与极化强度有关的任何电荷密度分布不能对绝缘体提供净电荷。我们往往发现需要用不连续函数表示极化强度。例如,在被自由空间包围的物质中,象图6.0. 1.中的球,极化强度在界面处能从-个有限值降为零。在这种区域中,可以有面极化电荷密度。怀着要从P确定此电荷密度的目的,式(6)可以对包围界而的增量面积的药丸盒积分。当进行-P→esE和 p>p的替代时,式(6)取与高斯定律相同的形式,所以证明过程与从式(1.3. 1)导出(1.3.17)是相同的。我们得出结论,在P的法向分量有跃变的地方,就有面极化电荷密度。(7)n.(P-P)G=-正如式(6)告诉我们在材料的体积内怎样对于已知P的分布确定极化电荷密度,这个表达式可用来计算在界面处极化电荷密度的奇异性(面极化电荷密度)。注意按照式(6),P起源于负极化电荷而终止于正电荷。这与E和电荷密度间的关系相反。图6.,1. 2直圆柱体的均匀极化引起的极化面电荷。例如,按照(6)和(7)两式,示于图6.1.2中均勾极化的材料圆柱休,当P向上指时,在顶部有正0s,而负的在底部。161 :

6.2 存在极化时的定律与连续性条件当不成对的和极化的电荷密度区分开时,高斯定律变成(1)V'erE=pup,这里式(6.1.6)使p与P相关(2)P,--V.P因为P是每单位体积“平均"的极化量,它是在原子尺度上的位置的“平滑”失量函数。在这个意义上,它是一个宏观变量。它的散度的负值,即极化电荷密度,也是一个宏观量,它不反映微观电荷分布的“粒度”。这样,因为它出现在式(1)中,电场强度也是一个宏观变量。象获得式(1.3.7)那样,进行式(1)对包围界面的一部分的增量体积的积分,结果是(3)n·E(E*-Eb)=0.u+am这里式(6. 1.7)使0sp与P相关g,=-n. (Pa-Pb)(4)这最后的两个等式分别给出在不连续的表面上,高斯定律式(1)的连续性条件。极化电流密度与安培定律高斯定律不是受到极化影响的仪有的定律。如果极化强度随时间变化,则穿过6.1节中所述的面 S的电荷流动构成电流。因此我们需要研究电荷守恒,并且更一般地研究时变极化强度对安培定律的影响。为此,下面的步骤能导得用时变极化强度表示的极化电流密度。按照6.1节中得出的P的定义,极化过程中通过表面的面元da转移电荷量dQ?dQ=P.da这可以根据图6.2.1所示的体积d·da能大致预见。如果极化强度P随时间变化,则按照此等式,()K电荷以有限的速率通过面元。对于qNd或P变茅推王化AP,通过增量面元da的电荷最为A(dQ) =△P.da6)图6.2.1电荷通过面元da引起极化电流密度2注意在此表示式中我们有两个微分标记。 d表示Q是微分的这一事实,因为da 是微分。1dQ随时间的变化率,△(dQ)/At可以用电流di,表示,它从(b)这一边通过da到(a)这一边。di,-A(do)- P.da(7)A偏微分符号用来把对t的微分与P的空间依从关系区别开。通过面元da的电流di通常写成电流密度点乘da(8)di,=J,-da出此我们比较最后这两个式了,并导出极化电流密度是162