西安交通大学：《电磁场与电磁能》课程教学资源（PPT课件）第一章 静电场

第一章 静电场 序 电场强度 静电场环路定律、高斯定律 静电场基本方程、分界面上的衔接条件 静电场边值问题、唯一性定理 分离变量法 有限差分法 ○○○○○ 镜像法和电轴法 电容和部分电容 静电能量与力

第一章 静电场

合D第一章静电场●静电场：相对观察者静止且量值不随时间变化的电荷所产生的电场。。本章任务：阐述静电荷与电场之间的关系，在已知电荷或电位的情况下求解电场的各种计算方法，或者反之。静电场知识结构框图·静电场是本课程的基础。由此建立的物理概念、分析方法在一定条件下可类比推广到恒定电场，恒定磁场及时变场

第一章 静 电 场 • 静电场： 相对观察者静止且量值不随时间变化的电荷所产生的电场。 • 本章任务： 阐述静电荷与电场之间的关系，在已知电荷或电位的情况下求解 电场的各种计算方法，或者反之。 • 静电场是本课程的基础。由此建立的物理概念、分析方法在一 定条件下可类比推广到恒定电场,恒定磁场及时变场。 • 静电场知识结构框图

合KD1.1.电场强度1.1.1 库仑定律库仑定律是静电现象的基本实验定律。大量试验表明：真空中两个静止的点电荷1与92之间的相互作用力：9192.E12F2, = N(牛顿)O4元0R2R9Fiz2 = 9192. E21N(牛顿)4元R2F2, = -F12图1.1.1两点电荷间的作用力适用条件·两个可视为点电荷的带电体之间相互作用力；10-9·无限大真空情况（式中80=8.85×10-l2F/m)36元*可推广到无限大各向同性均匀介质中（→）思考当真空中引入第三个点电荷9：时，试问,与92相互间的作用力改变吗？为什么？结论：电场力符合失量叠加原理

1.1.1 库仑定律 1.1 电场强度 2 12 0 1 2 21 4 R q q e F =    N( 牛顿) F21 = −F12 适用条件 • 两个可视为点电荷的带电体之间相互作用力; • 无限大真空情况 (式中 可推广到无限大各向同性均匀介质中 12 9 8.85 10 36 10 − − = =    0 F/m) ( ) 0  → 2 21 0 1 2 12 4 R q q e F =    N( 牛顿) 结论：电场力符合矢量叠加原理 图1.1.1 两点电荷间的作用力 库仑定律是静电现象的基本实验定律。大量试验表明: 真空中两个静止 的点电荷 q1 与 q2 之间的相互作用力: 当真空中引入第三个点电荷 时，试问 与 相互间的作用力改 变吗? 为什么？ 3 q 1 q 2 q

AKKD112请静电场基本物理量电场强度F(X,y,=)定义： E(x,y,=)=limV/m (N/C)qi90电场强度（Electric Field Intensity）E表示单位正电荷在电场中所受至的力（F），它是空间坐标的失量函数，定义式给出了E的大小、方向与单位。a）点电荷产生的电场强度ZAFqeEp(r):V/m4neoze,qtFqr-rqyE,(r)=q480r-r-rq(r)q(r-r')-I=RZ4元80r-r个p(r)qy4TE,REeRV/m图1.1.2点电荷的电场

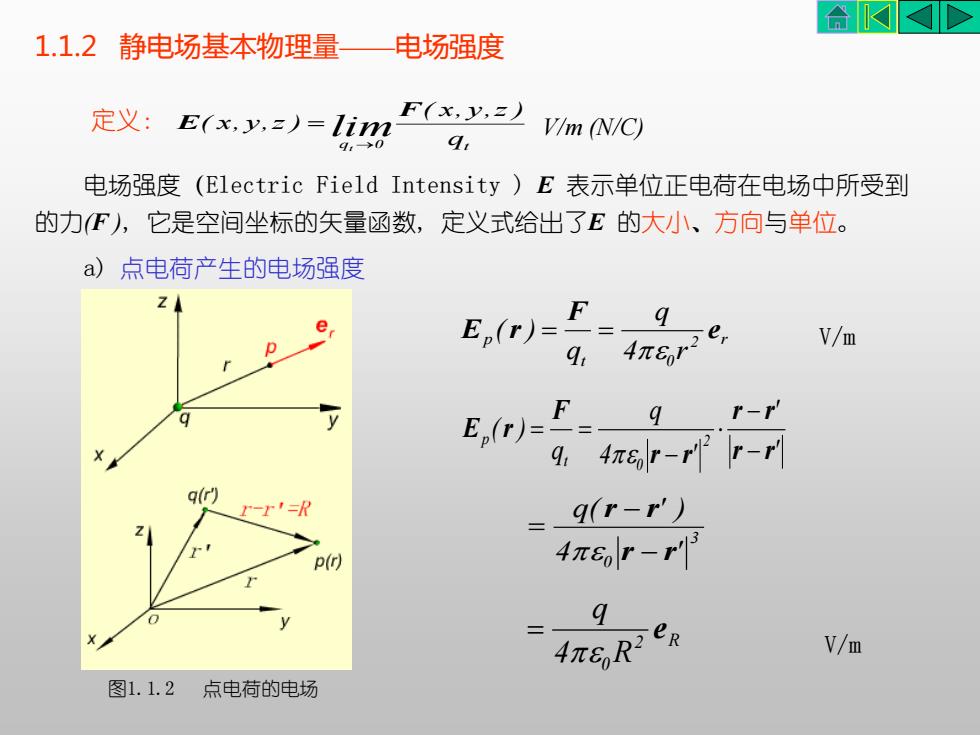
1.1.2 静电场基本物理量——电场强度 定义： q 0 qt ( x, y,z ) ( x, y,z ) lim t F E → = V/m (N/C) 电场强度（Electric Field Intensity ) E 表示单位正电荷在电场中所受到 的力(F ), 它是空间坐标的矢量函数, 定义式给出了E 的大小、方向与单位。 a) 点电荷产生的电场强度 2 r t 0 p 4 r q q ( ) e F E r   = = V/m ' ' 4 ' q q ( ) 2 0 t p r r r r r r F E r − −  − = =   3 0 4 ' q( ' ) r r r r − − =   2 R 4 0 R q e   = V/m 图1.1.2 点电荷的电场

合KDb）n个点电荷产生的电场强度（注意：矢量叠加）1Nqkqkr-rE(r).eV/m4元8r-r'4元%Rkrc)连续分布电荷产生的电场强度1r-r'dE(r)dq(r')4元8-P(r)dvR=r-rdq = p(r' )dV'体电荷分布P(r)-E(r)do4元80rr1P(r')dy图1.1.3体电荷的电场eRR?4元80面电荷分布线电荷分布dq = o(r')ds'dq = t(r')dlo(r)ds'1t(r')dlE(r)E(r)eReRJR2R?4元4元8

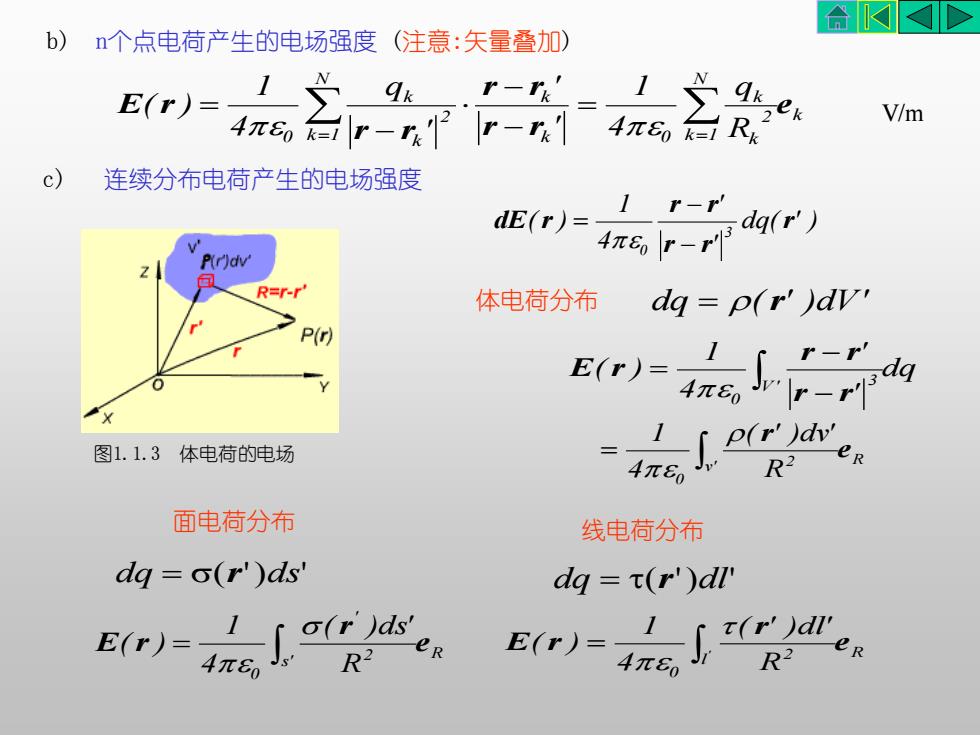
b) n个点电荷产生的电场强度 (注意:矢量叠加) c) 连续分布电荷产生的电场强度 dq( ' ) ' ' 4 1 ( ) 3 0 r r r r r dE r − − =   k N k 1 2 k k k 0 k N k 1 2 k k 0 R q 4 1 ' ' ' q 4 1 ( ) e r r r r r r E r   = = = − −  − =     V/m 体电荷分布 dq = (r' )dV' dq ' ' 4 1 ( ) V' 3 0  − − = r r r r E r   R v' 2 0 R ( ' )dv' 4 1 e r  =    面电荷分布 R s' 2 ' 0 R ( )ds' 4 1 ( ) e r E r  =    dq = (r')ds' 线电荷分布 R l 2 0 ' R ( ' )dl' 4 1 ( ) e r E r  =    dq = (r')dl' 图1.1.3 体电荷的电场