第五章准静态电磁场 5.0序 5.1电准静态场和磁准静态场 5.2磁准静态场与集总电路 5.3电准静态场与电荷驰豫 5.4集肤效应与邻近效应 5.5涡流及其损耗 5.6导体的交流内阻抗 5.7电磁兼容简介 E =yE, 0 H x
第五章 准静态电磁场
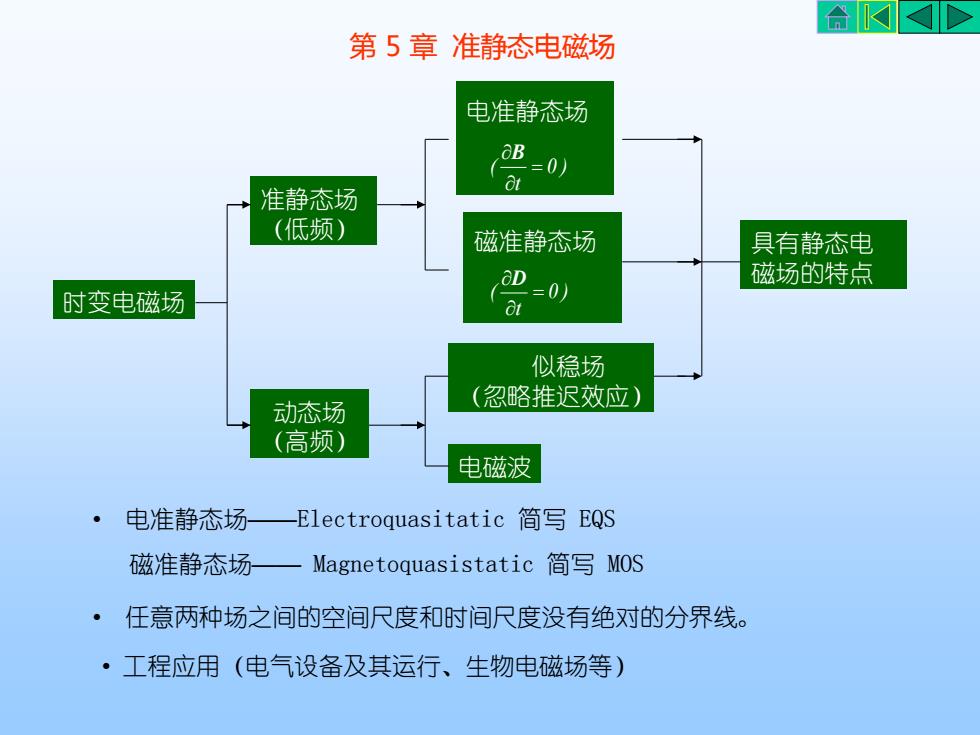
AKK第5章准静态电磁场电准静态场OB=0)at准静态场(低频)磁准静态场具有静态电磁场的特点aD=0)时变电磁场at似稳场(忽略推迟效应)动态场(高频)电磁波电准静态场-Electroquasitatic简写EQS磁准静态场一Magnetoquasistatic 简写 Mos·任意两种场之间的空间尺度和时间尺度没有绝对的分界线。工程应用(电气设备及其运行、生物电磁场等)
第 5 章 准静态电磁场 • 电准静态场——Electroquasitatic 简写 EQS 磁准静态场—— Magnetoquasistatic 简写 MOS • 任意两种场之间的空间尺度和时间尺度没有绝对的分界线。 • 工程应用(电气设备及其运行、生物电磁场等) 电准静态场 0 ) t ( = B 准静态场 (低频) 时变电磁场 磁准静态场 0 ) t ( = D 具有静态电 磁场的特点 动态场 (高频) 似稳场 (忽略推迟效应) 电磁波

合KKD5.1电准静态场和磁准静态场aB(=0)的作用,即E,~0,电磁场基本方程为低频时,忽略二次源电准静态场ataDdpV.B=0,V.J--VxH=J+atCVxE=0,V.D=p特点:电场的有源无旋性与静电场相同,称为电准静态场(EQS)。用洛仑兹规范V·A=-o/ot,得到动态位满足的微分方程VA=-w,Vp=-p/saD磁准静态场低频时,忽略二次源的作用,即H,0,电磁场基本方程为atVxH=J.V.B=0,V-J=0VxE=-oB/ot,V.D=p特点:磁场的有旋无源性与恒定磁场相同,称为磁准静态场(MQS)。用库仑规范V·A=0,得到动态位满足的微分万程V'A=-, V'=-p/8
电 准 静 态 场 特点: 电场的有源无旋性与静电场相同,称为电准静态场(EQS)。 用洛仑兹规范 A = − t ,得到动态位满足的微分方程 , / 2 2 A = − J = − 低频时,忽略二次源 的作用,即 ,电磁场基本方程为 t D HD 0 = − = = = E B D H J B J / t , , 0 , 0 特点:磁场的有旋无源性与恒定磁场相同,称为磁准静态场(MQS)。 磁 准 静 态 场 低频时,忽略二次源 的作用,即 0, ( 0 ) Ei t = B = = = − = + E D B J D H J 0 , t , 0 , t 电磁场基本方程为 A = 0 , / 2 2 A = − J = − 用库仑规范 ,得到动态位满足的微分 方程 5.1 电准静态场和磁准静态场

AKK讨论与引伸EQS 与MQS 的共性与个性A.Q满足泊松方程,说明EQS和MQS忽略了滞后效应和波动性,属于似稳场。·EQS和MQS场中,同时存在着电场与磁场,两者相互依存。:EQS场的电场与静电场满足相同的基本方程,在任一时刻t,两种电场的分布致,解题方法相同。EQS的磁场按v×H=J+aD/at计算。MQS的磁场与恒定磁场满足相同的基本方程,在任一时刻t,两种磁场的分布一致,解题方法相同,MQS的电场按×E=-aB/at计算。·A.在两种场中满足相同的微分方程,描述不相同的场,为什么?a)A的散度不同,A必不相同,B=V×A也不相同;b)E=-V(EQS)和E=-Vβ-aA/at(MQS),表明E不相同
· A, 满足泊松方程,说明 EQS 和 MQS 忽略了滞后效应和波动性,属于似稳场。 · EQS和MQS 场中,同时存在着电场与磁场,两者相互依存。 · EQS场的电场与静电场满足相同的基本方程,在任一时刻 t ,两种电场的分布 一致,解题方法相同。EQS的磁场按 H = J +D t 计算。 · MQS的磁场与恒定磁场满足相同的基本方程,在任一时刻 t ,两种磁场的分布 一致,解题方法相同,MQS的电场按 E = −B t 计算。 · A, 在两种场中满足相同的微分方程,描述不相同的场,为什么? b) E = − (EQS)和 E = − −A t (MQS),表明 E 不相同。 a)A的散度不同,A 必不相同, B = A 也不相同; EQS 与 MQS 的共性与个性
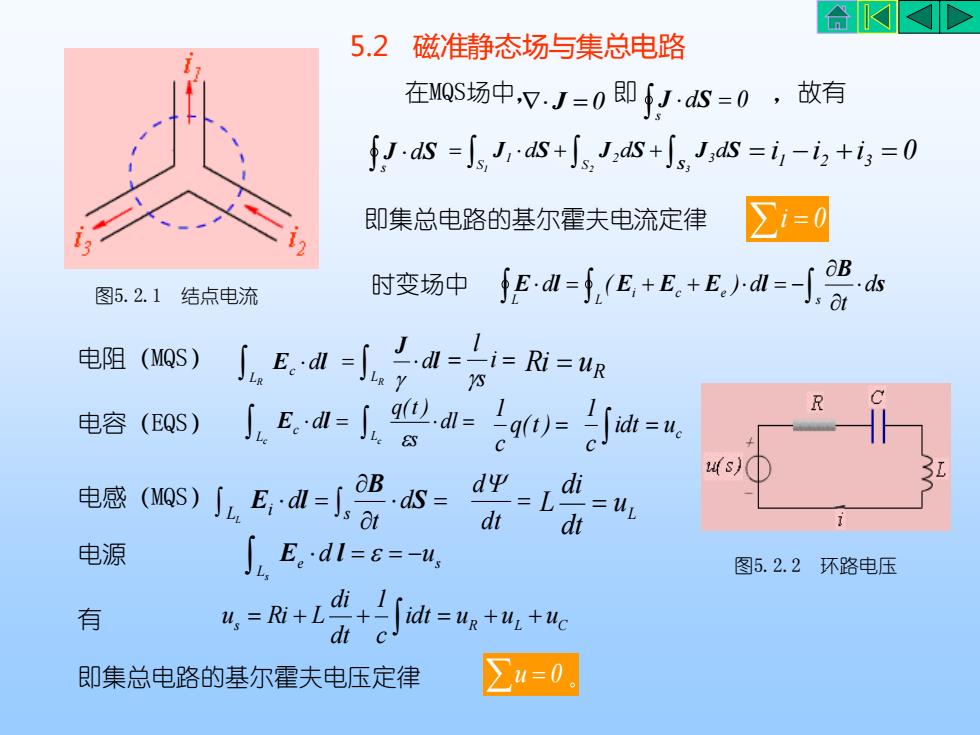
合KKD52元磁准静态场与集总电路在MQS场中,v.J=0即{J·dS=0 ,故有fJ.ds =J,Jrds+Js,Jds+J,Jds=i,-i, +i,=0i=0即集总电路的基尔霍夫电流定律aB时变场中 fE·dl-f,(E,+E.+E.)·dl =-.d图5.2.1结点电流atJ. E.dl =]., 二.dl ==i= Ri =uR电阻(MQS)AR[, E,dl= [, 9d= Lq(0)= idt=u电容(EQS)Sus)dyrdiaB.ds =C电感(MQS)JE,·dl=JI=uadtdt电源E.dl=8=-u,图5.2.2环路电压,= R+L+ [udt=ug+u,+te有dtCZu=0即集总电路的基尔霍夫电压定律
5.2 磁准静态场与集总电路 在MQS场中, J =0 即 d 0 ,故有 s = J S J dS s J S J S J S S d d d 1 2 3 3 S 2 S 1 = + + = i 1 −i 2 +i 3 = 0 即集总电路的基尔霍夫电流定律 i = 0 时变场中 = + + = − L s i c e L d t d ( ) d s B E l E E E l 电容(EQS) = Lc c E dl = Lc dl s q(t ) q(t ) = c 1 c idt u c 1 = 电阻(MQS) LR c E dl = LR dl J = i = s l R Ri = u 电感(MQS) = = S B E l d t d L s i L = dt d L u dt di L = 电源 s L e d u s = = − E l 有 s R L C idt u u u c 1 dt di u = Ri + L + = + + 即集总电路的基尔霍夫电压定律 = u 0 图5.2.1 结点电流 图5.2.2 环路电压