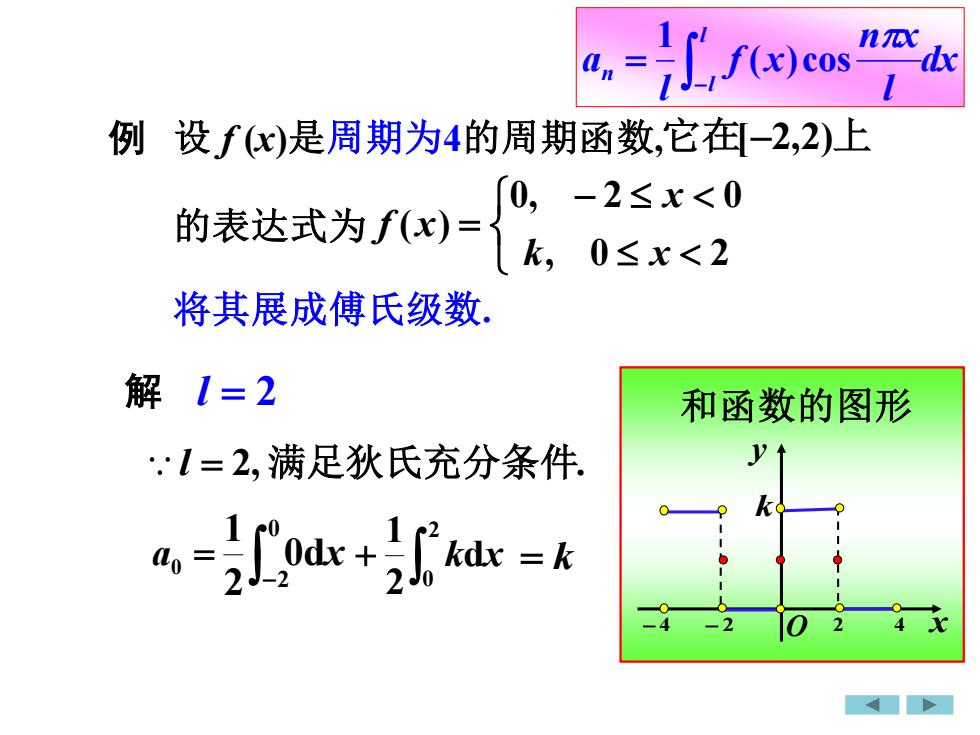
nTx=f(x)cosdxa,n1例 设,f(x)是周期为4的周期函数,它在[-2,2)上[0,-2≤x<0的表达式为,f(x)=k, 0≤x<2将其展成傅氏级数解 [=2和函数的图形y:l=2.满足狄氏充分条件FOdx +kdx = k2 Jo2J7
解 l = 2, 满足狄氏充分条件. a0 = = k dx l n x f x l a l l n − = ( )cos 1 l = 2 − 0 2 0d 2 1 x + 2 0 d 2 1 k x 例 将其展成傅氏级数. − = , 0 2 0, 2 0 ( ) k x x f x 它在[−2,2)上 f (x)的图形 k O x y − 4 − 2 2 4 和函数的图形 k O x y − 4 − 2 2 4 设 f (x)是周期为4的周期函数, 的表达式为
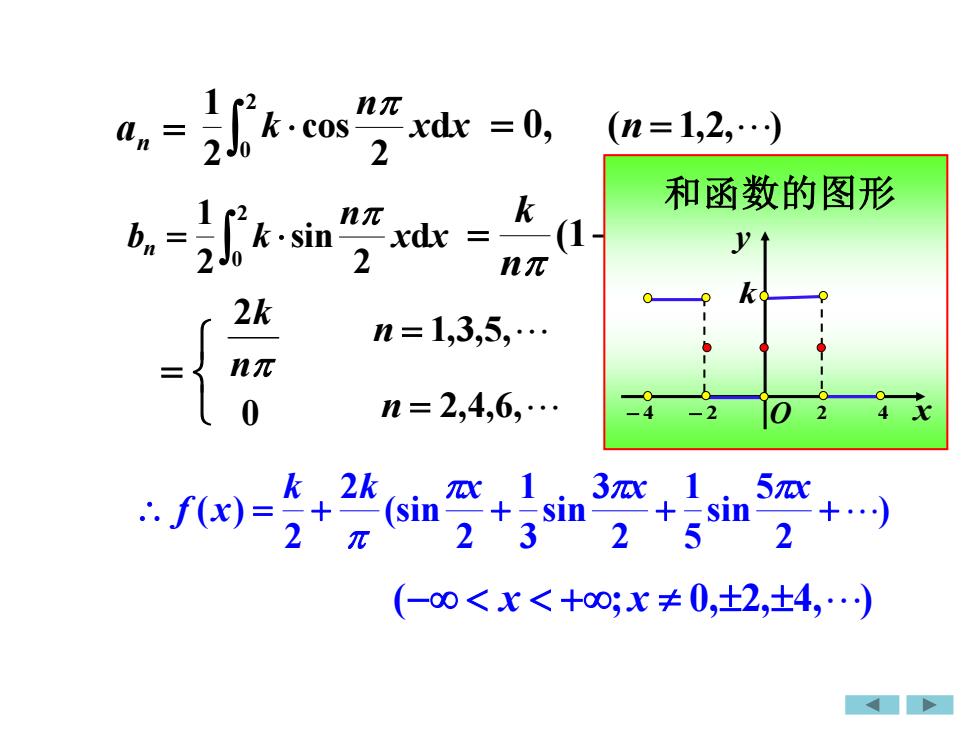
1n元= 0,k.cosxdx(n = 1,2,..)2n22 Jo和函数的图形k2n元k·sin1xdx22 Jon元2kn =1,3,5, .n元n = 2,4,6, .:01024-2X42kk13元x15元XTx(sinsinsin: f(x) =+.222325元(-80 < x< +80; x ± 0,±2,±4,.)
2 0 d 2 cos 2 1 x x n k = 0, = 2 0 d 2 sin 2 1 x x n bn k (1 cos ) n n k = − = ) 2 5 sin 5 1 2 3 sin 3 1 2 (sin 2 2 ( ) = + + + + k k x x x f x (− x +; x 0,2,4, ) an = (n = 1,2, ) n = 1,3,5, n 2k 0 n = 2,4,6, 和函数的图形 k O x y − 4 − 2 2 4