《线性代数》课程教学课件（PPT讲稿，C）矩阵的分块法

1 0 0 0 0 0 A= 1 0 b E 0 1 1 0 00 即 A- a 0 1 0 b 1 上页 回

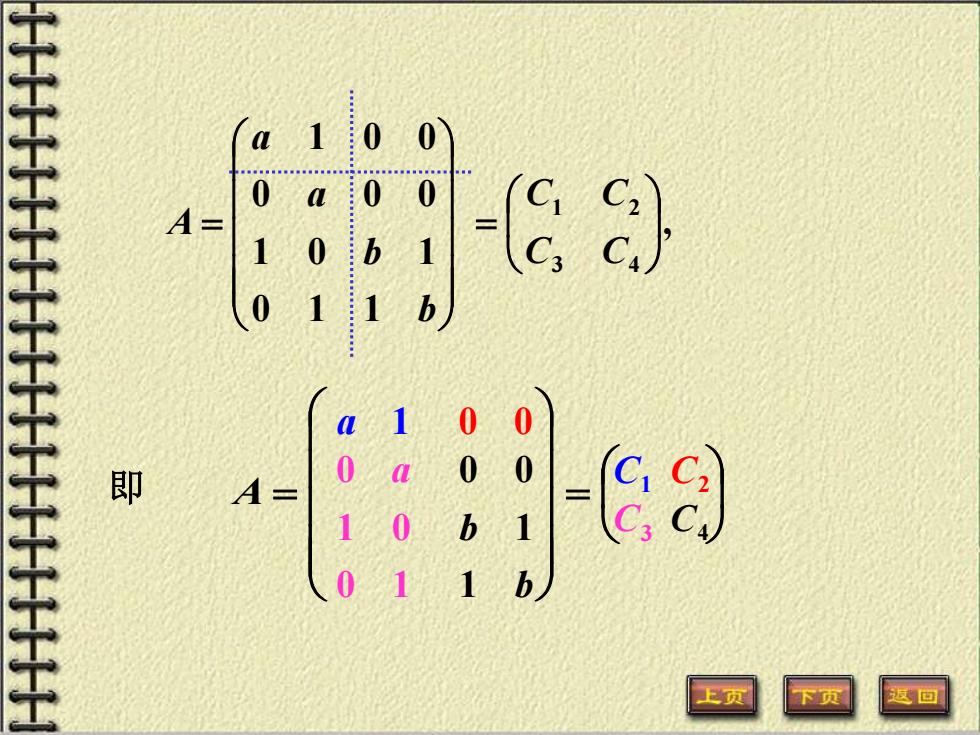
              = b b a a A 0 1 1 1 0 1 0 0 0 1 0 0 , 3 4 1 2       = C C C C       =               A = a 1 C1 0 0 C2 0 1 1 0 0 a C3 b b 1 1 0 0 C4 即

0 a 0 0 A= 1 0 b 1 a-6） 0 :1 b 1 0 0 0 0 A- 0 0 b =(44,A 0 注：分块时首先满足E,再考虑对角或三角矩阵 然后考虑以及其它的特殊矩阵

,      = E B A O ( ) 1 2 3 4 = A A A A ,               = b b a a A 0 1 1 1 0 1 0 0 0 1 0 0               = b b a a A 0 1 1 1 0 1 0 0 0 1 0 0 1 0 a A a   =           = b b B 1 1       = 0 1 1 0 E       = 0 0 0 0 O 1 0 1 0 a A     =                      = 1 0 1 2 a A               = 1 0 0 3 b A               = b A 1 0 0 4 注：分块时首先满足 E ，再考虑对角或三角矩阵， 然后考虑 O 以及其它的特殊矩阵

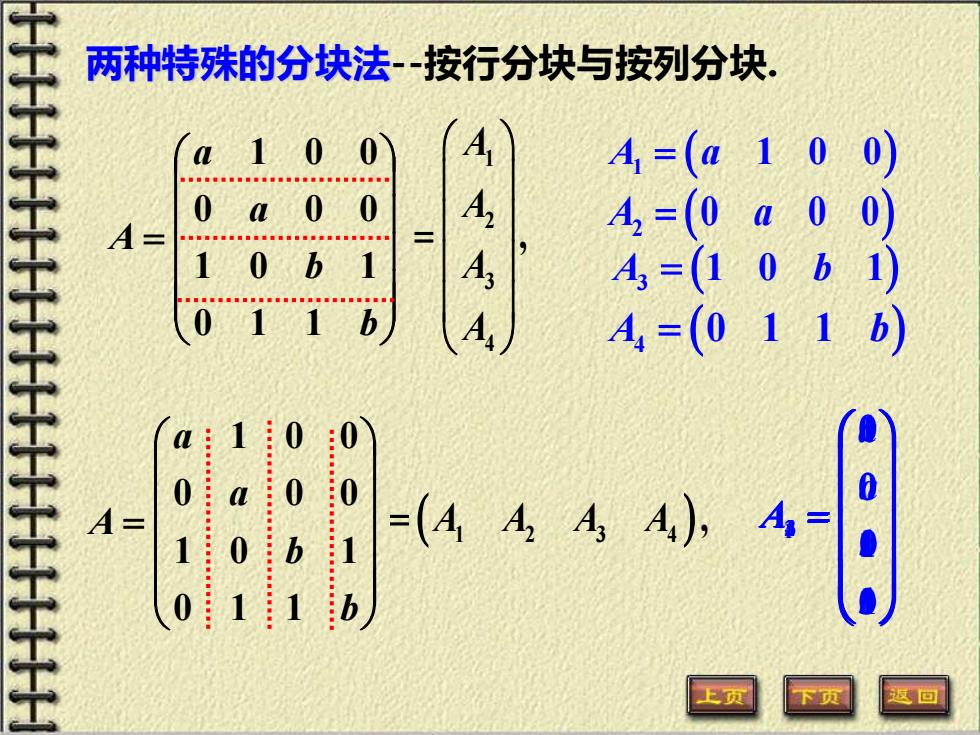
两种特殊的分块法-按行分块与按列分块。 A,=(a100) 0 L 0 0 A 0 A- 4=(0a 0) 1 0 b A A,=10b 01 A=(011b) 0 0 a 0 0 A- b A)= 01 b 上页

              = b b a a A 0 1 1 1 0 1 0 0 0 1 0 0 两种特殊的分块法-按行分块与按列分块. 1 2 3 4 , A A A A     =         ( ) 1 A a = 1 0 0 ( ) 2 A a = 0 0 0 ( ) 3 A b = 1 0 1 ( ) 4 A b = 0 1 1 ( ) 1 2 3 4 = A A A A ,               = b b a a A 0 1 1 1 0 1 0 0 0 1 0 0 1 0 1 0 a A     =                      = 1 0 1 2 a A               = 1 0 0 3 b A               = b A 1 0 0 4

二、 分块矩阵的运算规则 分块矩阵的运算规律与普通矩阵规律运算相类似. 1、矩阵的加法 设与为同型矩阵，采用相同的分块法，有 其中A与 沟同型矩阵，则 Au+Bu . A+B= A1+B1.A B

11 11 1 1 1 1 . r r s s sr sr A B A B A B A B A B   + +   + =       + + 11 1 11 1 1 1 , r r s sr s sr A A B B A B A A B B         = =             1、矩阵的加法 设 A 与 B 为同型矩阵，采用相同的分块法，有 其中 Aij 与 B 为同型矩阵，则 ij 分块矩阵的运算规律与普通矩阵规律运算相类似. 二、分块矩阵的运算规则