
例 3计算由曲线y2=2x和直线y=x4所围成的图形的面积解两曲线的交点=xy2 = 2xy=x-4=2x→ (2,-2), (8,4) yE[-2,4]选为积分变量dA = 18.dA =A:dyy+221
例 3 计算由曲线 y 2x 2 = 和直线 y = x − 4所围 成的图形的面积. 解 两曲线的交点 (2,−2), (8,4). = − = 4 2 2 y x y x 选 y 为积分变量 y[−2, 4] dy y dA y = + − 2 4 2 18. 4 2 = = − A dA y 2x 2 = y = x − 4 6

x = p(t)如果曲边梯形的曲边为参数方程y=y(t)曲边梯形的面积A:y(t)p'(t)dt.(其中t,和t,对应曲线起点与终点的参数值)在[tj,t,](或[t,,l)上x=(t)具有连续导数,y=y(t)连续
如果曲边梯形的曲边为参数方程 = = ( ) ( ) y t x t 曲边梯形的面积 ( ) ( ) . 2 1 = t t A t t dt (其中 1 t 和 2 t 对应曲线起点与终点的参数值) 在[ 1 t , 2 t ](或[ 2 t , 1 t ])上x = (t)具有连续导数, y = (t)连续. 7

VX例4求椭圆1的面积ax=acost解椭圆的参数方程y=bsint由对称性知总面积等于4倍第一象限部分面积,A = 4[" ydx = 4[’ bsin td(acos t)A sin’ tdt = πab.: 4ab08
例 4 求椭圆 1 2 2 2 2 + = b y a x 的面积. 解 椭圆的参数方程 = = y b t x a t sin cos 由对称性知总面积等于4倍第一象限部分面积. = a A ydx 0 4 = 0 2 4 bsin td(acost) ab tdt = 2 0 2 4 sin = ab. 8
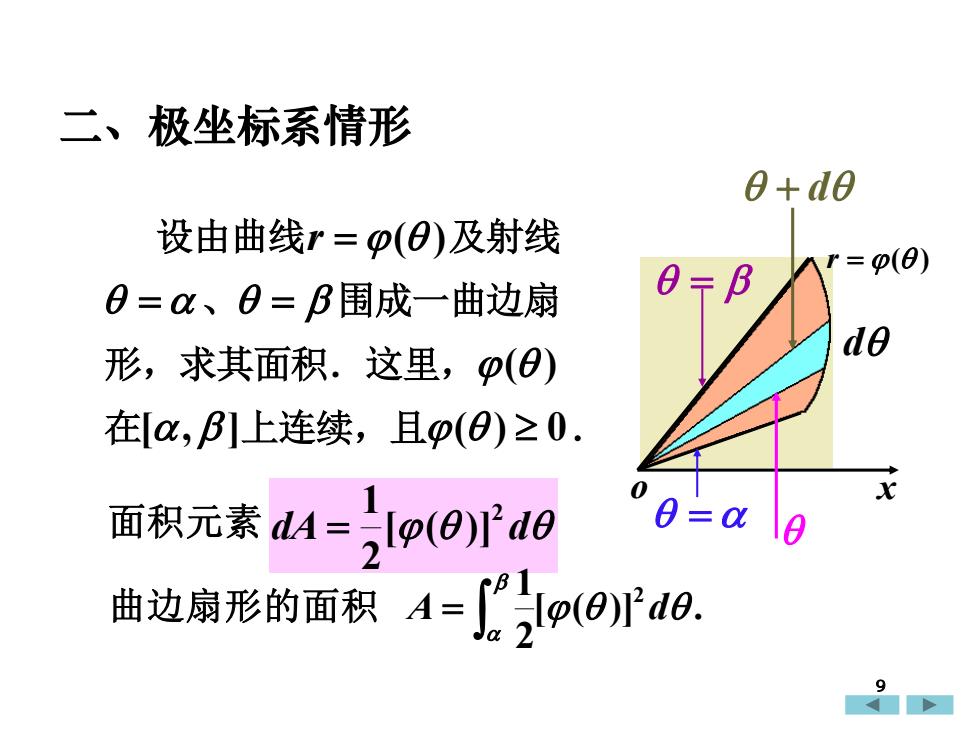
二、极坐标系情形e+de设由曲线r =β(O)及射线r =(0)θβ=α、=β围成一曲边扇de形,求其面积.这里,Φ()在[α,β]上连续,且Φ(①)≥0.x0=α面积元素dA=[(0)deAA= f"[p(0)do.曲边扇形的面积9
设由曲线r = ( )及射线 = 、 = 围成一曲边扇 形,求其面积.这里,( ) 在[, ]上连续,且( ) 0. o x = d = + d 面积元素 dA d 2 [ ( )] 2 1 = 曲边扇形的面积 [ ( )] . 2 1 2 A d = 二、极坐标系情形 r = ( ) 9
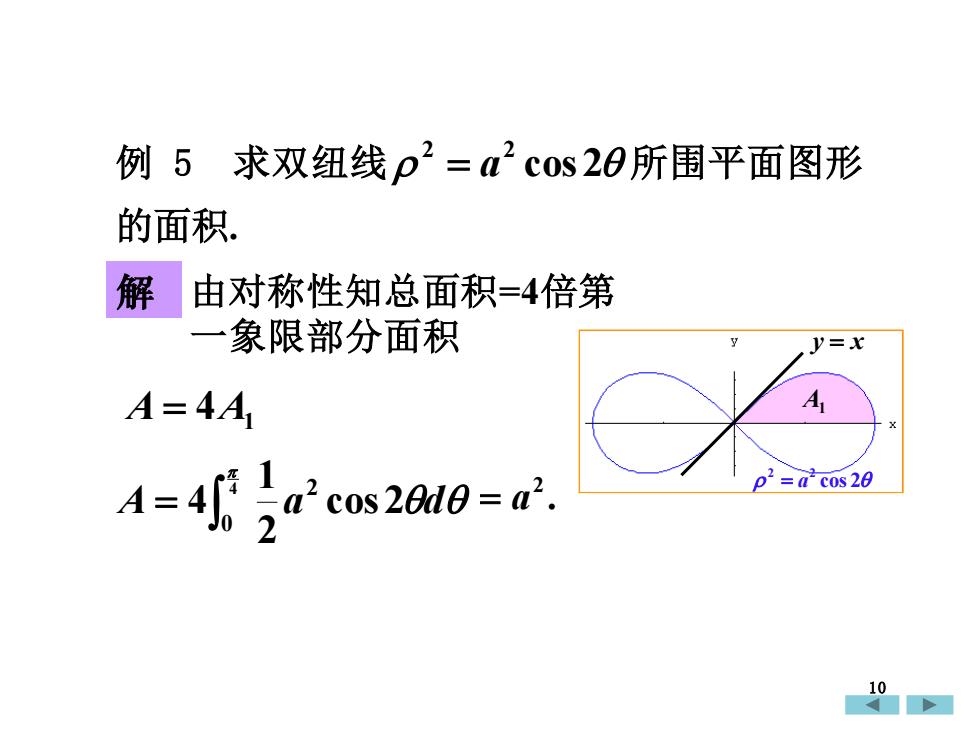
例5求双纽线p2=α2cos20所围平面图形的面积。解由对称性知总面积=4倍第一象限部分面积V=xAA=4Ao* =acos20cos 2Ad = a?0210
例 5 求双纽线 cos 2 2 2 = a 所围平面图形 的面积. 解 由对称性知总面积=4倍第 一象限部分面积 A = 4A1 A a cos 2 d 2 1 4 4 0 2 = . 2 = a y = x cos 2 2 2 = a A1 10