
Zu, =u, +u, +u, +...+un, +... (l)n=1级数的敛散性它与部分和数列是否有极限是等价的对收敛级数(1),称差8ZuIn = S- Sn=un+1 +un+2 +.n+ii-1limr, = 0显然有为级数(1)的余项或余和n-00误差为rnl当n充分大时,Sn~s
n n r = s − s = un+1 + un+2 + = = + i 1 un i lim = 0 → n n r 对收敛级数(1), 为级数(1)的余项或余和.显然有 当n充分大时, 级数的敛散性它与部分和数列是否有 极限是等价的. = + + ++ + = n n un u1 u2 u3 u 1 (1) 称差 s s n 误差为 | | n r

例级数1+2+3++n+..的部分和n(n+1)S,=1+2+3+...+n=2n(n + 1)而lims, = lim82n-oon-→>所以,级数发散
例 2 ( 1) 1 2 3 + = + + + + = n n sn n 而 = → n n lims 所以, 级数 1+ 2 + 3 ++ n + 的部分和 = + → 2 ( 1) lim n n n 级数发散

例讨论等比级数(几何级数)8Zaq" = a+aq+aq" +...+aq" +... (a* O)n=0的收敛性。(重要)解如果g1时1-Sn = a+aq+aq’ +...+aqna-aqaaq1-q1-q1-q
解 如果q 1 时 2 −1 = + + + + n sn a aq aq aq q a aqn − − = 1 q aq q a n − − − = 1 1 (重要) 例 讨论等比级数(几何级数) 的收敛性. ( 0) 2 0 = + + + + + = aq a aq aq aq a n n n
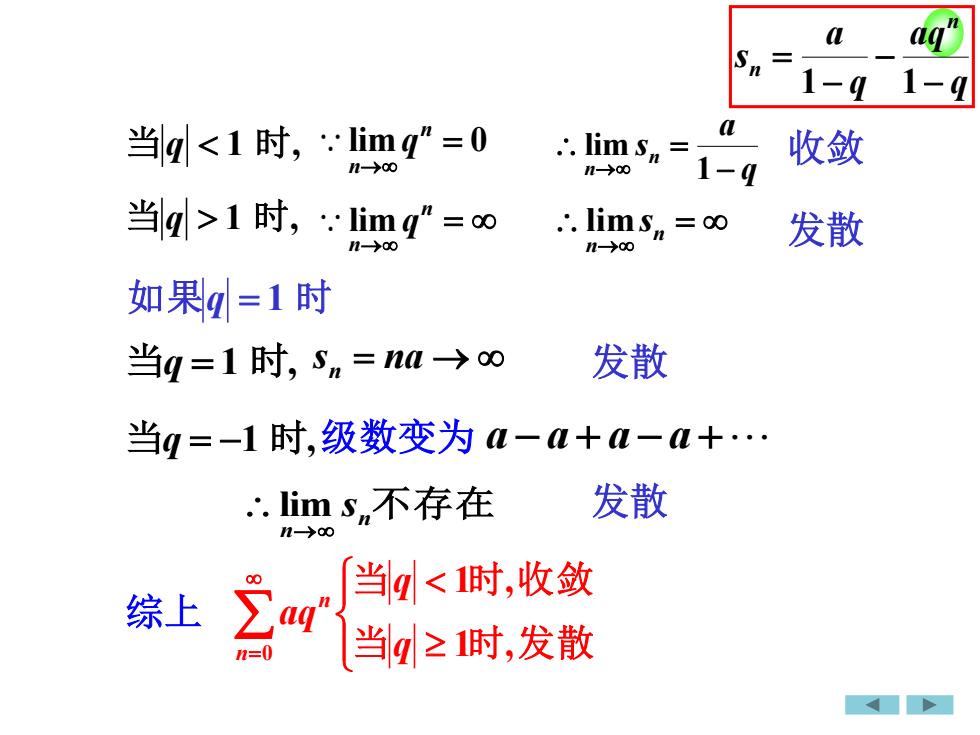
naaqSn1-q1-qa当q<1时,: limq"= 0收敛. lim s1-qn>80n-00当q|>1 时,: lim"= 0:. lims, = 00发散n-0n-0如果=1 时发散当g=1时, Sn = na →80当q=-1时,级数变为a-a+a-a+.发散:lim s.不存在n>当<时,收敛8Zag"综上当q≥1时,发散n=0
当q 1 时, lim = 0 → n n q q a sn n − = → 1 lim 当q 1 时, = → n n lim q = → n n lims 收敛 发散 如果q = 1 时 当q = 1 时, 当q = −1 时, sn = na → 发散 a − a + a − a + n 不存在 n s → lim 发散 综上 = 当 时 发 散 当 时 收 敛 1 , 1 , 0 q q aq n n 级数变为 q aq q a s n n − − − = 1 1

8例讨论级数3ln"a(a>0)的敛散性>n=18Z3ln"a是以lna为公比的等比级数因为解n=1故当-<a<e时,Ilnakl,级数收敛.或a≥e时,llna≥l,发散当0<a≤=D当<1时,收敛8Zag"当≥1时,发散n=0
讨论级数 3ln ( 0) 的敛散性. 1 = a a n n 解 例 因为 =1 3ln n n a 是以 lna 为公比的等比级数, 故 , 1 当 a e时 e | lna | 1, 级数收敛. 发散. e a 1 当0 | lna | 1, = 当 时 发 散 当 时 收 敛 1 , 1 , 0 q q aq n n 或a e时