
第一章函数与极限 习题1-1 1.求下列函数的自然定义域: (1)y=√3x+2: (2)y=1- (3)y=: (4)y- 1 (5)y=sinV压; (6)y=tan(x+1) (7)y=arcsin(x-3); (8)y=√/3-+aretan- (9)y=ln(x+1) (10)y=e 2.下列各题中,函数八x)和g(x)是否相同?为什么? (1)f(x)=Igx,g(x)=21gx: (2)f(x)=,g(x)=√震: (3)(x)=-x,g(x)=xx-; (4)f(x)=1.g(x)=see'x-tan'x. 3.设 sinx,l<号 p(x)= 0,1x≥ 求()()(平)(-2),并作出函数y=()的图形 4.试证下列函数在指定区间内的单调性: (1)y=产x(-0,1): (2)y=x+lnx,(0,+m). 5.设八x)为定义在(-,)内的奇函数,若八x)在(0,)内单调增加,证明(x)在(-l,0) 内也单调增加. 6.设下面所考虑的函数都是定义在区间(-山,)上的.证明: (1)两个偶函数的和是偶函数,两个奇函数的和是奇函数; (2)两个偶函数的乘积是偶函数,两个奇函数的乘积是偶函数,偶函数与奇函数的乘积 是奇函数 7.下列函数中哪些是偶函数,哪些是奇函数,哪些既非偶函数又非奇函数? (1)y=x2(1-x2): (2)y=3x2-x a话 (4)y=x(x-1)(x+1): (5)y=sin x-cos x+1; (6)y=a ·16·

第一节映射与函数 8.下列各函数中哪些是周期函数?对于周期函数,指出其周期: (1)y=co8(x-2): (2)y=cos 4x; (3)y=1+sin x: (4)y=x08x: (5)y=sin'x. 9.求下列函数的反函数 (1)y=x*1: 2)y 6)y22(ad-c0: (4)y=2sin3x(8≤x≤): (5)y=1+n(x+2): (6)y=2+ 0.设函数八x)在数集X上有定义,试证:函数八x)在X上有界的充分必要条件是它在 X上既有上界又有下界 11.在下列各题中,求由所给函数构成的复合函数,并求这函数分别对应于给定自变量 值x,和x的函数值: (Dy=,u=in=石4= (2)y=m,=2=8名=牙 (3)y=m,u=1+x2,x,=1,=2: (4)y=e,4=x2,x1=0,x2=1; (5)y=u2,u=e,x,=1,x2=-1. 12.设八x)的定义域D=[0,1],求下列各函数的定义域 (1)fx2): (2)f(sin x); (3)f(x+a)(a>0): (4)fx+a)+x-a)(a>0) 13.设 r1,lx1<1, fx)=0,1x=1,g(x)=e -1,1x1>1, 求几g(x)]和g(x)],并作出这两个函数的图形. 14.已知水渠的横断面为等腰梯形,斜角p=40°(图1-20).当过水断面ABCD的面积为 定值S。时,求湿周L(L=AB+BC+CD)与水深h之间的函数关系式,并指明其定义域 15.设x0平面上有正方形D=1(x,y)1 0≤x≤1,0≤y≤1|及直线1:x+y=t(1≥0). 若S()表示正方形D位于直线1左下方部分 的面积,试求S()与之间的函数关系 16.求联系华氏温度(用F表示)和摄氏 图1-20 温度(用C表示)的转换公式,并求 ·17·
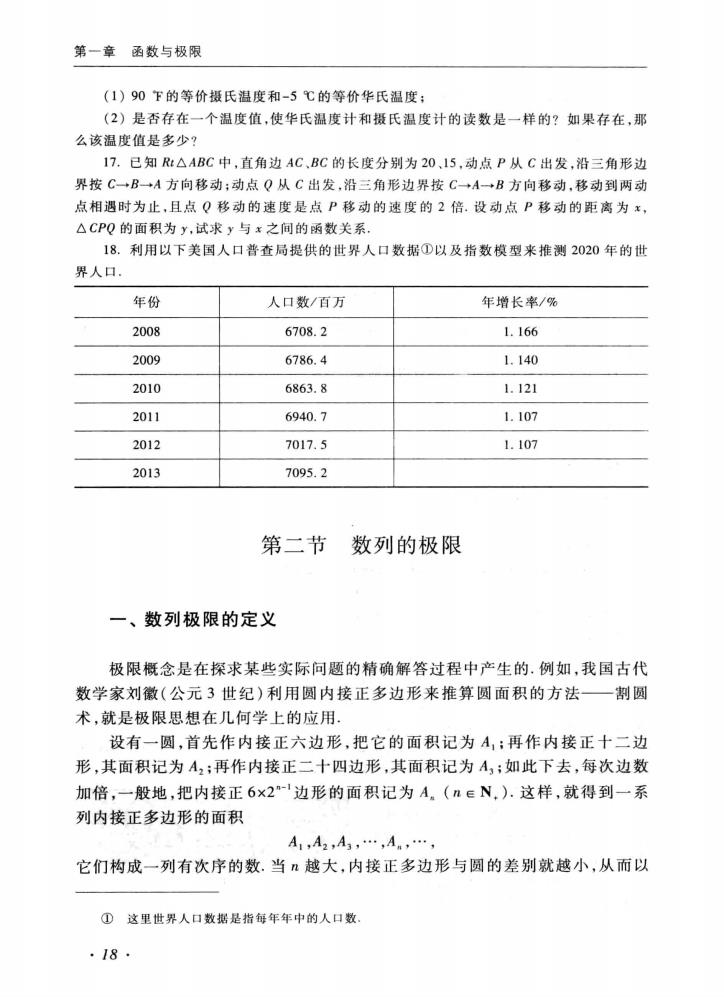
第一章函数与极限 (1)90℉的等价摄氏温度和-5℃的等价华氏温度: (2)是否存在一个温度值,使华氏温度计和摄氏温度计的读数是一样的?如果存在,那 么该温度值是多少? 17.已知:△ABC中,直角边AC,BC的长度分别为20,15,动点P从C出发,沿三角形边 界按C一B一A方向移动;动点Q从C出发,沿三角形边界按C一→A一→B方向移动,移动到两动 点相遇时为止,且点Q移动的速度是点P移动的速度的2倍。设动点P移动的距离为x, △CPQ的面积为y,试求y与x之间的函数关系. 18.利用以下美国人口普查局提供的世界人口数据①以及指数模型来推测2020年的世 界人口. 年份 人口数/百万 年增长率/% 2008 6708.2 1.166 2009 6786.4 1.140 2010 6863.8 1.121 2011 6940.7 1.107 2012 7017.5 1.107 2013 7095.2 第二节数列的极限 一、数列极限的定义 极限概念是在探求某些实际问题的精确解答过程中产生的.例如,我国古代 数学家刘徽(公元3世纪)利用圆内接正多边形来推算圆面积的方法 一割圆 术,就是极限思想在几何学上的应用 设有一圆,首先作内接正六边形,把它的面积记为A:再作内接正十二边 形,其面积记为A2;再作内接正二十四边形,其面积记为A,;如此下去,每次边数 加倍,一般地,把内接正6×2-边形的面积记为A(neN,.这样,就得到一系 列内接正多边形的面积 A1,A2,A3,.,Am,., 它们构成一列有次序的数.当越大,内接正多边形与圆的差别就越小,从而以 ①这里世界人口数据是指每年年中的人口数 ·18·

第二节数列的极限 A,作为圆面积的近似值也越精确.但是无论n取得如何大,只要n取定了,A,终 究只是多边形的面积,而还不是圆的面积因此,设想n无限增大(记为n→∞,读 作n趋于无穷大),即内接正多边形的边数无限增加,在这个过程中,内接正多边 形无限接近于圆,同时A.也无限接近于某一确定的数值,这个确定的数值就理 解为圆的面积.这个确定的数值在数学上称为上面这列有次序的数(所谓数列) A,A2,A,.,A.,.当n一→∞时的极限.在圆面积问题中我们看到,正是这个数列 的极限才精确地表达了圆的面积. 在解决实际问题中逐渐形成的这种极限方法,已成为高等数学中的一种基 本方法,因此有必要作进一步的阐明。 先说明数列的概念.如果按照某一法则,对每个n∈N,对应着一个确定的 实数x,这些实数x按照下标n从小到大排列得到的一个序列 x1,2,x3,.,x,. 就叫做数列,简记为数列{x,{. 数列中的每一个数叫做数列的项,第n项x,叫做数列的一般项(或通项) 例如: 12,3 23,4,.n+. 2,4,8,.,2°,. 1,1 1,-1,1,.,(-1)1, 2分.a4-) n 都是数列的例子,它们的一般项依次为 n中T,2,是,(-1)4,+-1) 在几何上,数列x}可看作数轴上的一个动点,它依次取数轴上的点x,x2 x3,.,.(图1-21) 数列{x,}可看作自变量为正整数n的函数 药”文 x=f(n),neN. 图1-21 当自变量n依次取1,2,3,.一切正整数时,对应的函数值就排列成数列 {xn}. 对于我们要讨论的问题来说,重要的是:当n无限增大时(即n→∞时),对 应的x。=f八)是否能无限接近于某个确定的数值?如果能够的话,这个数值等 于多少? .19

第一章函数与极限 我们对数列 2分营*0 (2-1) n 进行分析.在这数列中, -巴=1*(-) n 我们知道,两个数a与b之间的接近程度可以用这两个数之差的绝对值 lb-a来度量(在数轴上lb-a表示点a与点b之间的距离),lb-al越小,a与b 就越接近. 就数列(2-1)来说,因为 -=-)-2 由此可见,当n越来越大时,一越来越小,从而x,就越来越接近于1.因为只要n 足够大,x。-1山即。可以小于任意给定的正数,所以说,当n无限增大时,无限 接近于1例如,给定d0欲使。0只要n>10,即从第101项起,都能使不等 1x.-11<100 成立.同样地,如果给定1000那么从第1001项起,都能使不等式 1x.-11<10000 成立.一般地,不论给定的正数ε多么小,总存在着一个正整数N,使得当n>N 时,不等式 Ix.-11<E 都成立.这就是数列三,=n+(-1)(a=1,2.)当n一m时无限接近于1这件 n 事的实质.这样的-个数1,叫做数列.-+(-)(a=1,2,.)当n一时的 极限 一般地,有如下数列极限的定义: 定义设{x,{为一数列,如果存在常数a,对于任意给定的正数6(不论它 多么小),总存在正整数N,使得当n>N时,不等式 ·20·