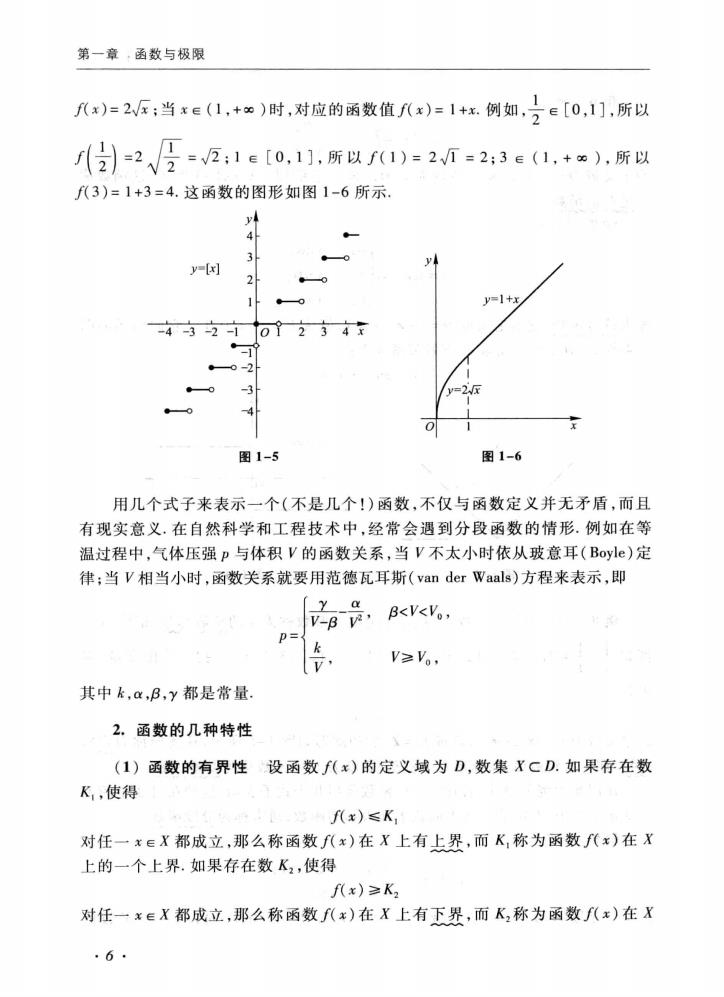
第一章,函数与极限 x)=2;当xe(1,+女)时,对应的函数值f(x)=1+x例如,2∈[0,1],所以 份)-2=21e[0,1,所以f1)=2=2:3e1,+).所以 f(3)=1+3=4.这函数的图形如图1-6所示 34 y-(x] 2 y=1+灯 -4-3-2-02方4x 。-0-2 图1-5 图1-6 用几个式子来表示一个(不是几个!)函数,不仅与函数定义并无矛盾,而且 有现实意义.在自然科学和工程技术中,经常会遇到分段函数的情形.例如在等 温过程中,气体压强p与体积V的函数关系,当V不太小时依从玻意耳(Boyle)定 律;当V相当小时,函数关系就要用范德瓦耳斯(van der Waals)方程来表示,即 g是.a<e p= k V. V≥V。, 其中k,a,B,y都是常量 2.函数的几种特性 (1)函数的有界性设函数f(x)的定义域为D,数集XCD.如果存在数 K,使得 f代x)≤K, 对任一x∈X都成立,那么称函数f(x)在X上有上界,而K,称为函数f(x)在X 上的一个上界.如果存在数K,使得 f(x)≥K2 对任一x∈X都成立,那么称函数f(x)在X上有下界,而K,称为函数f(x)在X ·6

第一节映射与函数 -1 图1-12 (4)函数的周期性设函数八x)的定义域为D.如果存在一个正数1,使得 对于任一xeD有(x±l)∈D,且 f代x+l)=f八x) 恒成立,那么称f(x)为周期函数,1称为f(x)的周期,通常我们说周期函数的 周期是指最小正周期, 例如,函数sinx,cosx都是以2π为周期的周期函数;函数tanx是以r为周 期的周期函数。 图1-13表示周期为1的一个周期函数.在每个长度为1的区间上,函数图形 有相同的形状, 图1-13 并非每个周期函数都有最小正周期.下面的函数就属于这种情形. 例l0狄利克雷(Dirichlet)函数 D(x)=11.EQ. 10,xEQ 容易验证这是一个周期函数,任何正有理数,都是它的周期.因为不存在最 小的正有理数,所以它没有最小正周期. 3.反函数与复合函数 作为逆映射的特例,我们有以下反函数的概念 设函数f人:D一→f(D)是单射,则它存在逆映射∫':(D)→D,称此映射∫'为函 9

第一章函数与极限 数f的反函数 按此定义,对每个yef(D),有唯一的x∈D,使得f八x)=y,于是有 f'(y)=x. 这就是说,反函数∫的对应法则是完全由函数∫的对应法则所确定的, 例如,函数y=x,x∈R是单射,所以它的反函数存在,其反函数为 x=y寸,yeR. 由于习惯上自变量用x表示,因变量用y表示,于是y=x,x∈R的反函数通 常写作y=x了,xeR. 一般地,y=fx),xeD的反函数记成y=∫(x),xef(D), 若f是定义在D上的单调函数,则f:D→f(D)是单射,于是f的反函数∫'必 定存在,而且容易证明f'也是f八D)上的单调函数.事实上,不妨设∫在D上单调 增加,现在来证明∫在f(D)上也是单调增加的 任取y,2∈f(D),且y,<y2按函数∫的定义,对y,在D内存在唯一的原像 x,使得f(x)=,于是∫(y)=x1;对y2,在D内存在唯一的原像x2,使得f(x2) =y2,于是f(y2)=x2 如果x1>x2,则由f八x)单调增加,必有y>y2:如果x1=x2,则显然有y,=y2.这 两种情形都与假设y,<y不符,故必有x,<x2,即∫'(y)<f'(y).这就证明了∫ 在f(D)上是单调增加的. 相对于反函数y=∫'(x)来说,原来的函数y=(x)称为直接函数.把直接函 数y=(x)和它的反函数y=∫'(x)的图形画在同一坐标平面上,这两个图形关于 直线y=x是对称的(图1-14).这是因为如果P(a,b)是y=f(x)图形上的点,则 有b=f(a).按反函数的定义,有a=∫'(b),故Q(b,a)是y=f'(x)图形上的点;反 之,若Q(b,a)是y=f'(x)图形上的点,则P(a,b)是y=f(x)图形上的点.而P(a b)与Q(b,a)是关于直线y=x对称的. 复合函数是复合映射的一种特例,按照通常 y-f(x) 函数的记号,复合函数的概念可如下表述: 设函数y=f(u)的定义域为D,函数u=g(x) y=f(x) Q(ba) 的定义域为D,且其值域R,CD,则由下式确定 的函数 (ab y=fg(x)],xED, 称为由函数u=g(x)与函数y=f(u)构成的复盒 函数,它的定义域为D,变量u称为中间变量. 图1-14 函数g与函数∫构成的复合函数,即按“先g后"的次序复合的函数,通常 ·10·

第一节映射与函数 上的一个下界.如果存在正数M,使得 (x)1≤M 对任一x∈X都成立,那么称函数f(x)在X上有界.如果这样的M不存在,就称 函数f八x)在X上无界;这就是说,如果对于任何正数M,总存在x,∈X,使 f(x)I>M,那么函数(x)在X上无界 例如,就函数f八x)=snx在(-,+)内来说,数1是它的一个上界,数-1 是它的一个下界(当然,大于1的任何数也是它的上界,小于-1的任何数也是它 的下界).又 Isin xl≤l 对任一实数x都成立,故函数f(x)=sinx在(-∞,+∞)内是有界的.这里M=1 (当然也可取大于1的任何数作为M而使(x)1≤M对任一实数x都成立) 又如函数(x)=在开区间(0,1)内没有上界,但有下界,例如1就是它的 一个下界,函数八x)=在开区间(0,1)内是无界的,因为不存在这样的正数 M,使≤M对于(0,1)内的一切x都成立.但是(x)=在区间(1,2)内是 有界的,例如可取M=1而使≤1对于一切xe(1,2)都成立. 容易证明,函数(x)在X上有界的充分必要条件是它在X上既有上界又有 下界. (2)函数的单调性设函数f(x)的定义域为D,区间ICD.如果对于区间1 上任意两点x,及x2,当x,<x,时,恒有 f(x,)<f(x2), 那么称函数f(x)在区间1上是单调增加的(图1-7);如果对于区间1上任意两 点x,及x2,当x,<x2时,恒有 f(x)>f2), 那么称函数(x)在区间1上是单调减少的(图1-8).单调增加和单调减少的函 数统称为单调函数, 例如,函数f(x)=x2在区间[0,+∞)上是单调增加的,在区间(-∞,0]上是 单调减少的;在区间(-∞,+∞)内函数f(x)=x2不是单调的(图1-9). 又例如,函数f(x)=x在区间(-x,+∞)内是单调增加的(图1-10) (3)函数的奇偶性设函数f(x)的定义域D关于原点对称.如果对于任 x∈D, f(-x)=f八x) 7
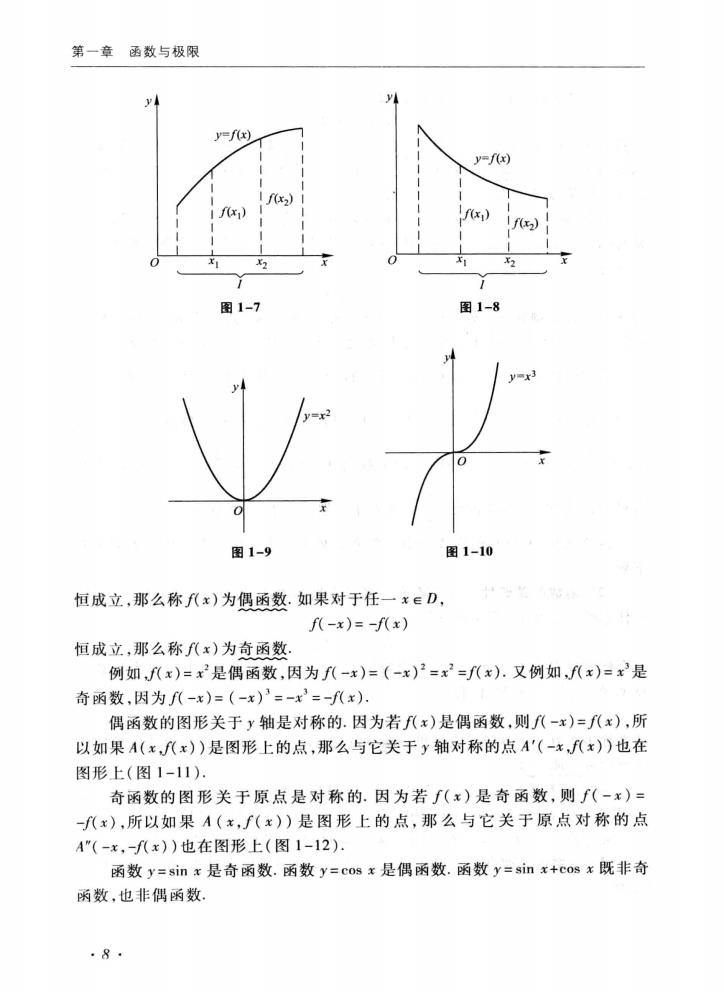
第一章函数与极限 y=f(x) y=f(x) 2) f) (x 图1-7 图1-9 图1-10 恒成立,那么称f八x)为偶函数.如果对于任一x∈D, f(-x)=-f(x) 恒成立,那么称f八x)为奇函数. 例如,f(x)=x是偶函数,因为f八-x)=(-x)2=x2=f(x).又例如,f(x)=x是 奇函数,因为f(-x)=(-x)=-x3=f(x). 偶函数的图形关于y轴是对称的.因为若f(x)是偶函数,则(-x)=(x),所 以如果A(x,(x)是图形上的点,那么与它关于y轴对称的点A'(-x,x))也在 图形上(图1-11). 奇函数的图形关于原点是对称的.因为若∫(x)是奇函数,则∫(-x)= -(x),所以如果A(x,∫(x)是图形上的点,那么与它关于原点对称的点 A"(-x,-f八x))也在图形上(图1-12) 函数y=sinx是奇函数.函数y=cosx是偶函数.函数y=sinx+cosx既非奇 函数,也非偶函数。 ·8