
利用DFT计算线性卷积一、两个有限长序列的线性卷积DFT(x[k] @ x2[k]= X,[m]X,[m]问题提出:LTI系统响应实际需要:y[K]=x [K]*h[k]可否利用DFT计算线性卷积?例: xi[K]={1,1,1}, x 2[K]={1,1,0,1} , N=4xi[k]*x2[k], x,[k]x2[k]7/2/2025通信、信息-2002
7/2/2025 通信、信息 -2002- 利用DFT计算线性卷积 问题提出: DFT [ ] [ ] [ ] [ ] x1 k x2 k = X1 m X2 m 实际需要: LTI系统响应 y[k]=x [k]h[k] 可否利用DFT计算线性卷积? 例:x1 [k]={1,1,1}, x 2 [k]={1,1,0,1} , N=4 一、两个有限长序列的线性卷积 [ ] [ ], [ ] [ ] 1 2 1 2 x k x k x k x k
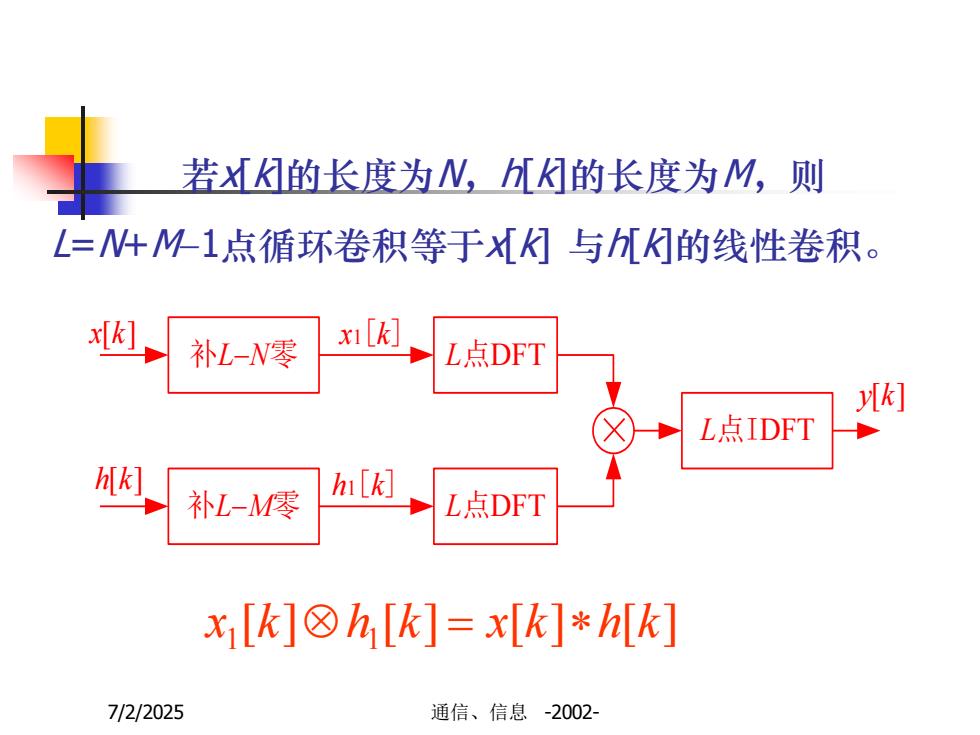
若xk的长度为N,hk的长度为M,则L=N+M-1点循环卷积等于XK与h[K的线性卷积xi [k]x[k]补L-N零L点DFTy[k]L点IDFTh[k]hi[k]补L-M零L点DFTxi[k] hi[k] = x[k] * h[k]7/2/2025通信、信息-2002-
7/2/2025 通信、信息 -2002- 若x[k]的长度为N,h[k]的长度为M,则 L=N+M-1点循环卷积等于x[k] 与h[k]的线性卷积。 补L-N零 补L-M零 L点DFT L点DFT L点IDFT x[k] h[k] y[k] x1[k] h1[k] [ ] [ ] [ ] [ ] 1 1 x k h k = x k h k

例:利用MATLAB由DFT计算x[K]*h[K]。x[k]={1, 2, 0, 1}, h[k]=[2, 2, 1, 1]%CalculateLinearConvolution byDFTx = [1 2 0 1];h = [2 2 1 1];% determine the length for zero paddingL = length(x)+length(h)-1;% Compute theDFTs by zero-paddingXE = fft(x,L);HE = fft(h,L);%Determine theIDFT of the producty1 = ifft(XE.*HE):7/2/2025通信、信息-2002-
7/2/2025 通信、信息 -2002- % Calculate Linear Convolution by DFT x = [1 2 0 1]; h = [2 2 1 1]; % determine the length for zero padding L = length(x)+length(h)-1; % Compute the DFTs by zero-padding XE = fft(x,L); HE = fft(h,L); % Determine the IDFT of the product y1 = ifft(XE.*HE); 例:利用MATLAB由DFT计算x[k]* h[k]。 x[k]={1, 2, 0, 1}, h[k]={2, 2, 1, 1}

长序列和短序列的线性卷积直接利用DFT计算的缺点:(1)信号要全部输入后才能进行计算,延迟太多(2) 内存要求大(3)算法效率不高解决问题方法:采用分段卷积分段卷积可采用重叠相加法和重叠保留法7/2/2025通信、信息-2002-
7/2/2025 通信、信息 -2002- 长序列和短序列的线性卷积 直接利用DFT计算的缺点: (1) 信号要全部输入后才能进行计算,延迟太多 (2) 内存要求大 (3) 算法效率不高 解决问题方法:采用分段卷积 分段卷积可采用重叠相加法 和 重叠保留法
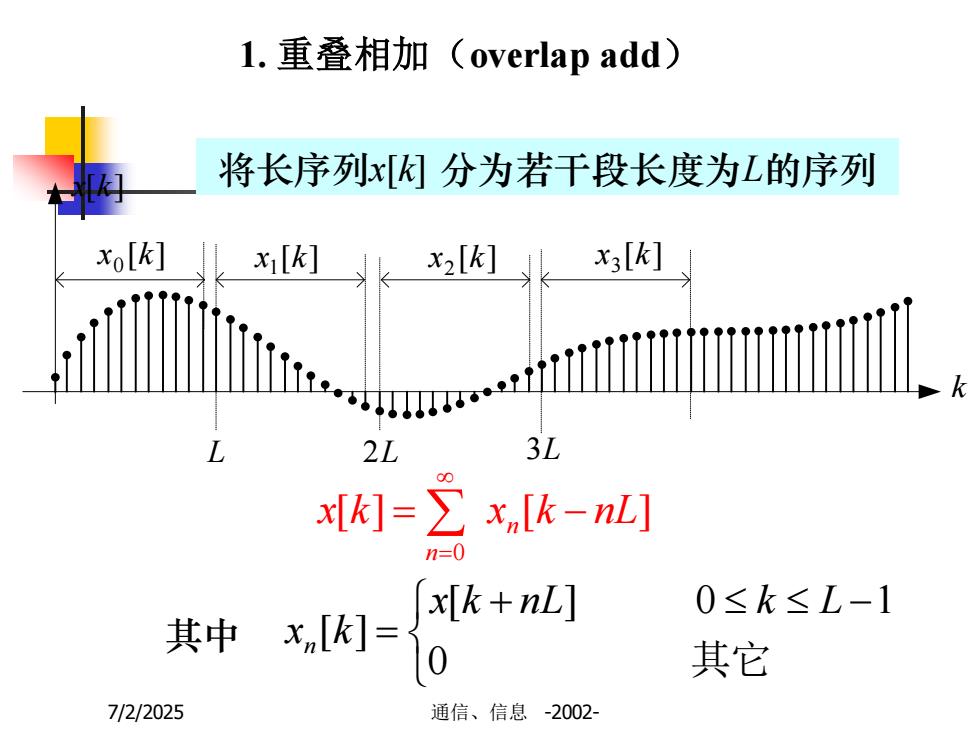
1.重叠相加(overlap add)将长序列x[Kl分为若于段长度为L的序列Kxo[k]x[k]x[k]x2[k]k3LL2L8Zx[k] =x,[k-nL]n=00≤k≤L-1x[k + nL]xn[k] =其中0其它7/2/2025通信、信息-2002-
7/2/2025 通信、信息 -2002- 1. 重叠相加(overlap add) 将长序列x[k] 分为若干段长度为L的序列 [ ] [ ] 0 x k xn k nL n = - = + - = 0 [ ] 0 1 [ ] 其它 x k nL k L x k n k x[k] [ ] 0 x k [ ] 1x k [ ] 2 x k [ ] 3 x k L 2L 3L 其中