
一、二阶和三阶行列式 类似以地,三元线性方程组 a11x1+a12X2+a13X3=b1, a21x1+a22X2+a23X3=b2, a31X1+a32x2+a33X3=b3 有解 x1=
类似地, 三元线性方程组 有解 一、二阶和三阶行列式
一、二阶和三阶行列式 其中 011 012.13 D 021 022 -023 31 32 、0331 =H23+22337+3252 -仔22牙-2开3好-开好2 称为三阶行列式, b1 a12 Q13 a11 b1 Q13 011 12 b1 D1= b2 a22 a23 D2 = a21 b2 Q23 D3= a21 a22 b3 032 Q33 a31 b3 d33 031 a32 bal
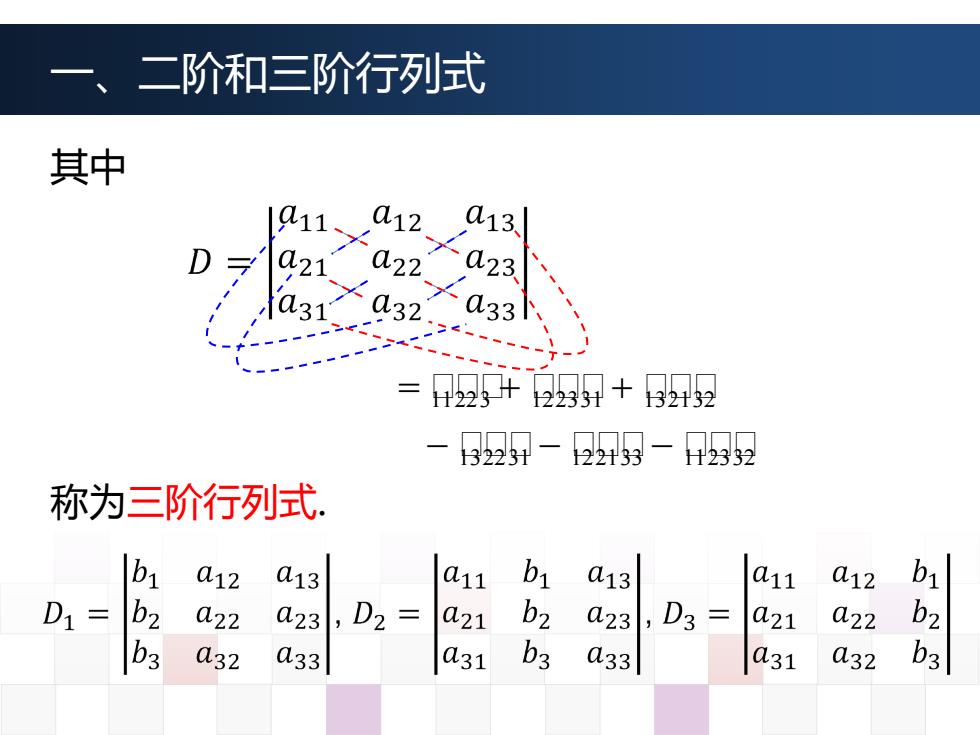
其中 称为三阶行列式. = ᵄ11ᵄ22ᵄ3 + ᵄ12ᵄ23ᵄ31 + ᵄ13ᵄ21ᵄ32 − ᵄ13ᵄ22ᵄ31 − ᵄ12ᵄ21ᵄ33 − ᵄ11ᵄ23ᵄ32 一、二阶和三阶行列式