
Mtndt(1) n=l,dt +R2+a0MbIn(t2 +a°) +-arctan-+C;2aabMtdtdt +(2) n>1,(t’ +a')"+a")"1tM1dt.2(n-1)(t" +a')~- +b]+a')"(t这三类积分均可积出,且原函数都是初等函数结论:有理函数的原函数都是初等函数
(2) n 1, 2 2 2 2 ( ) ( ) n n Mt b dt dt t a t a + + + 2 2 1 2( 1)( ) − − + = − n n t a M . ( ) 1 2 2 + + dt t a b n 这三类积分均可积出, 且原函数都是初等函数. 结论:有理函数的原函数都是初等函数. (1) n = 1, 2 2 2 2 Mt b dt dt t a t a + + + 2 2 ln( ) 2 M= + t a arctan ; b t C a a + +

1-dx.例2求积分21)x(x-)CB1A设++(x-1)2x(x-1)x-1x(1)1 = A(x -1)2 + Bx +Cx(x -1)代入特殊值来确定系数A.B,C取 x=0, =A=1 取x=1, →B=1并将 A,B 值代入(I) =C=-1取x=2,1111三一十x(x-1)?x(x-1)x-1
2 2 1 , ( 1) ( 1) 1 A B C x x x x x = + + − − − 设 2 1 ( 1) ( 1) (1) = − + + − A x Bx Cx x 代入特殊值来确定系数 A,B,C 取 x = 0, = A 1 取 x = 1, = B 1 取 x = 2, 并将 A B, 值代入 (1) = − C 1 2 1 1 1 . x x x ( 1) 1 = + − − − 2 1 x x( 1) − 例2 求积分 2 1 . ( 1) dx x x −
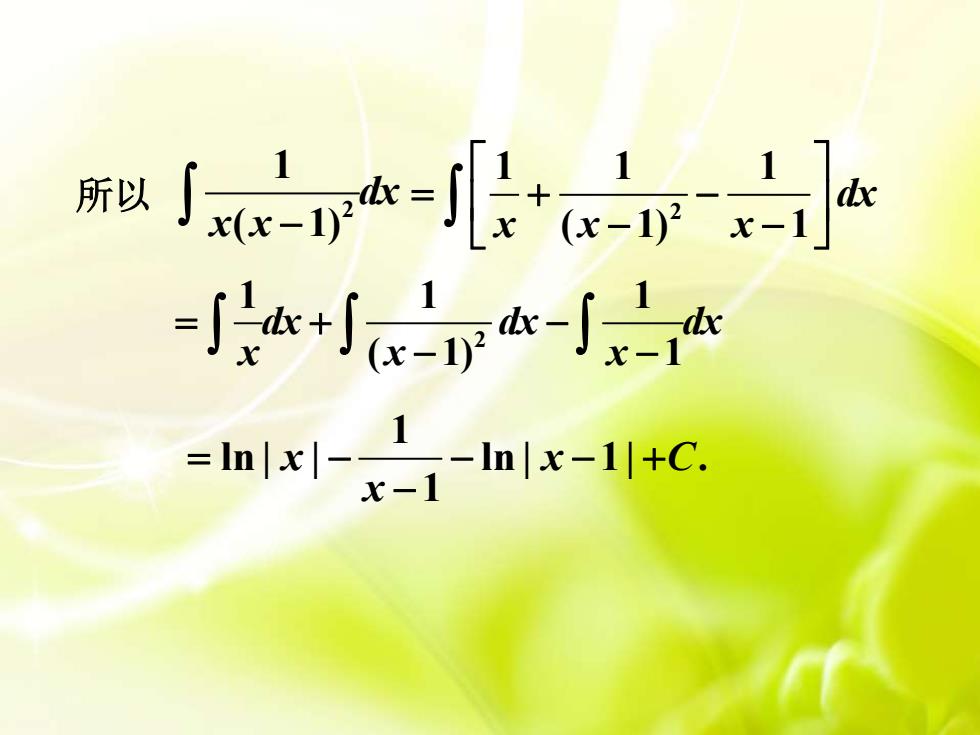
1元+7所以dxdx=(x-1)x(x-1)x-{-dx+dxdrxx= Inx|-In|x-1/+C.x-1
2 1 ( 1) dx x x − 2 1 1 1 ( 1) 1 dx x x x = + − − − 2 1 1 1 ( 1) 1 dx dx dx x x x = + − − − 1 ln | | ln | 1| . 1 x x C x = − − − + − 所以

1例3求积分dx.(1 + 2x)(1 + x)A1Bx + C设1+x?(1+2x)(1+x2) 1+2x1 = A(1+ x2)+(Bx + C)(1+2x),整理得 1=(A+2B)x2+(B+2C)x+C+A,A+2B=0,24B+2C = 0,BA5A+C=1,4215L41+2x1+(1 + 2x)(1+x)X
2 4 2 1 5 5 5 . 1 2 1 x x x − + = + + + 2 1 (1 ) ( )(1 2 ), = + + + + A x Bx C x 2 1 ( 2 ) ( 2 ) , = + + + + + A B x B C x C A 2 0, 2 0, 1, A B B C A C + = + = + = 4 2 1 , , , 5 5 5 = = − = A B C 2 2 1 , (1 2 )(1 ) 1 2 1 A Bx C x x x x + = + + + + + 设 2 1 (1 2 )(1 ) x x + + 整理得 例3 求积分 2 1 . (1 2 )(1 ) dx + + x x

所以dx(1 + 2x)(1 + x")24x+555T=[1+2xdxdx +2x22xdx +In |1+2x / -一-dx255.51+x1+X21I1+2x/-=In(1+arctanx + C.In15+55
所以 2 4 2 1 5 5 5 1 2 1 x dx dx x x − + = + + + 2 1 (1 2 )(1 ) dx + + x x 2 2 2 1 2 1 1 ln |1 2 | 5 5 1 5 1 x x dx dx x x = + − + + + 2 1 1 2 ln |1 2 | ln(1 ) arctan . 5 5 5 = + − + + + x x x C