
1dx.T例4求积分XItx+e61+e2 +e3 -6解 令t=e° →x=6lnt,dx=-dt,116dx = /dtX-xxI+t+t?+t t1+e? +e3 +e?133t + 36=6]dt :dtt(1 + t)(1 + t°)1+t?1+t
例4 求积分 解 . 1 1 2 3 6 dx e e e x x x + + + 6 6 6ln , , x t e x t dx dt t 令 = = = 3 2 2 3 6 1 1 6 1 1 x x x dx dt t t t t eee = +++ +++ 2 1 6 (1 )(1 ) dt t t t = + + 2 6 3 3 3 1 1 t dt t t t + = − − + +
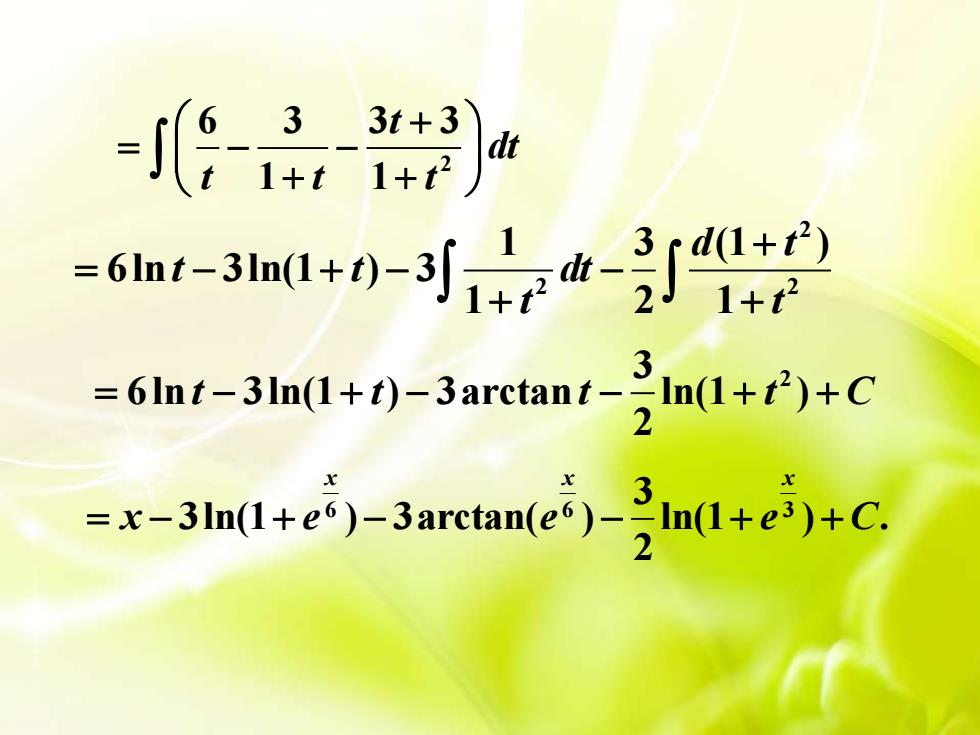
33t+31dt1+t?1+t3 r d(1+t2)= 6lnt - 3ln(1+t)-dt1+t?23-In(1 +t?)+C= 6lnt - 3ln(1+ t)- 3arctant -2xxX3=x-3ln(1+e)-3arctan(e)-=)In(1+e3)+C.2
3 2 6ln 3ln(1 ) 3arctan ln(1 ) 2 = − + − − + + t t t t C 2 6 3 3 3 1 1 t dt t t t + = − − + + 6 6 3 3 3ln(1 ) 3arctan( ) ln(1 ) . 2 x x x = − + − − + + x e e e C 2 2 2 1 3 (1 ) 6ln 3ln(1 ) 3 1 2 1 d t t t dt t t + = − + − − + +

说明:将有理函数分解为部分分式进行积分虽可行但不一定简便,因此要注意根据被积函数的结构寻求简便的方法例5. 求 1=[2x*+2x*+5x+5dx.x* +5x2 +42x2+5解: 1=[_2x*+5xdxdx4+5x2+44 +5x2 +4d(x* +5x + 4)(x2 +1)+ (x2 +4)dxx*+5x2+4(x2 +1)(x2 + 4)分项x==ln|x* + 5x? + 4|+=arctan+arctanx+C-22
2 2 d ( 1)( 4) x x x + + + 2 2 ( 1) ( 4) x x + + + 例5. 求 3 2 4 2 2 2 5 5 d . 5 4 x x x I x x x + + + = + + 3 4 2 2 5 d 5 4 x x I x x x + = + + 2 4 2 2 5 d 5 4 x x x x + + + + 4 2 4 2 1 d( 5 4) 2 5 4 x x x x + + = + + 1 4 2 ln 5 4 2 = + + x x 1 arctan 2 2 x + + + arctan x C 解: 说明: 将有理函数分解为部分分式进行积分虽可行, 但不一定简便 , 因此要注意根据被积函数的结构寻求 简便的方法. 分项

Y练习.求dx.福(x2 + 2x+2)(x2 +2x +2)-(2x+2)解:原式=dx(x2 +2x +2)dxd(x+2x+2)=[ (x+1° +1 (x2 + 2x+ 2)1+C= arctan(x+1) + x +2x+2
练习. 求 2 2 2 d . ( 2 2) x x x x + + 解: 原式 2 2 d ( 2 2) x x x = + + 2 ( 2 2) (2 2) x x x + + − + 2 d ( 1) 1 x x = + + 2 2 2 d( 2 2) ( 2 2) x x x x + + − + + = + arctan( 1) x 2 1 2 2 C x x + +

X例6 求dx100分析这是有理函数的积分.分母是100次多项式,如按部分分式法很麻烦.如作一个适当的变换使分母为单项,而分子为多项,除一下,化为和差的积分。解 作变换1一x=tr (1-t)2t +3dtdt :原式=一1001002dt9098100
例6 求 x x x d (1 ) 100 2 − 解 原式= 这是有理函数的积分. 如按部分分式法很麻烦. 使分母为单项, 作变换 1− x = t t t t d (1 ) 100 2 − − t t t t d 1 2 100 2 − + = − t t t t d 1 2 1 100 99 98 = − − + 分析 分母是100 次多项式, 如作一个适当的变换, 而分子为多项,除一下,化为和差 的积分