
有理函数化为部分分式之和的一般规律Q(x) = b,(x -a)~ ...(x -b)B(x? + px+g)~ ...(x? +rx+s)(1)分母中若有因式(x-a),则分解后为A2A,+(x-a)a-i(x-a)~x-a其中A,A,…,A,是常数A当α=1时,分解为x-a
(1)分母中若有因式 ( ) x a − ,则分解后为 1 2 1 , ( ) ( ) A A Ak x a x a x a − + + + − − − 有理函数化为部分分式之和的一般规律: 1 , ; A x a = − 当 时 分解为 1 2 , , , . 其中A A Ak是常数 0 2 2 ( ) ( ) ( ) ( ) ( ) Q x b x a x b x px q x rx s = − − + + + +

Q(x) = b,(x -a)~ ...(x -b)β(x? + px+g)~ ...(x? +rx+ s)(2)分母中若有因式(x2+px+g),其中p2-4q<0 则分解后为M,x+N,Mx+NM,x+ N,(x* + px+g)a- +(x + px +q)x*+ px+q其中M,N,是常数(i=1,2,…,2)Mx+ N特殊地:入=1,分解后为x? + px+q
(2)分母中若有因式 ,其中 2 ( ) x px q + + 则分解后为 2 p q − 4 0 1 1 2 2 2 2 1 2 ( ) ( ) M x N M x N M x N x px q x px q x px q − + + + + + + + + + + + + 特殊地: λ = 1, 分解后为 2 ; Mx N x px q + + + , ( 1,2, , ). M N i i i 其中 是常数 = λ 0 2 2 ( ) ( ) ( ) ( ) ( ) Q x b x a x b x px q x rx s = − − + + + +

真分式化为部分分式之和的待定系数法x+3Bx+3A例1x-5x+6(x-2)(x -3)x-3x-2x+3 = A(x-3)+B(x-2)x+3=(A+B)x-(3A+2B)A+B=1,A=-5UB=6-(3A + 2B) = 3,6-5x+3+x2 -5x+6x-3x-2
真分式化为部分分式之和的待定系数法 2 3 5 6 x x x + − + 3 ( 2)( 3) x x x + = − − , 2 3 A B x x = + − − x A x B x + = − + − 3 ( 3) ( 2), + = + − + x A B x A B 3 ( ) (3 2 ), 1, (3 2 ) 3, A B A B + = − + = 5 , 6 A B = − = 2 3 5 6 x x x + − + 5 6 . x x 2 3 − = + − − 例1

说明:将有理函数化为部分分式之和后,只出现三类情况:Mx + NA(3)(2)(1)多项式;(x + px +q)"(x-a)"Mx+ Ndx,讨论积分9)"(x2 + px +2Pp: x2+ px+q=x++q2-P-2令x+
说明: 将有理函数化为部分分式之和后,只出 现三类情况: (1) 多项式; (2) ; ( )n A x a − 2 (3) ; ( )n Mx N x px q + + + 讨论积分 2 , ( )n Mx N dx x px q + + + 2 2 2 , 2 4 p p x px q x q + + = + + − 令 t p x + = 2
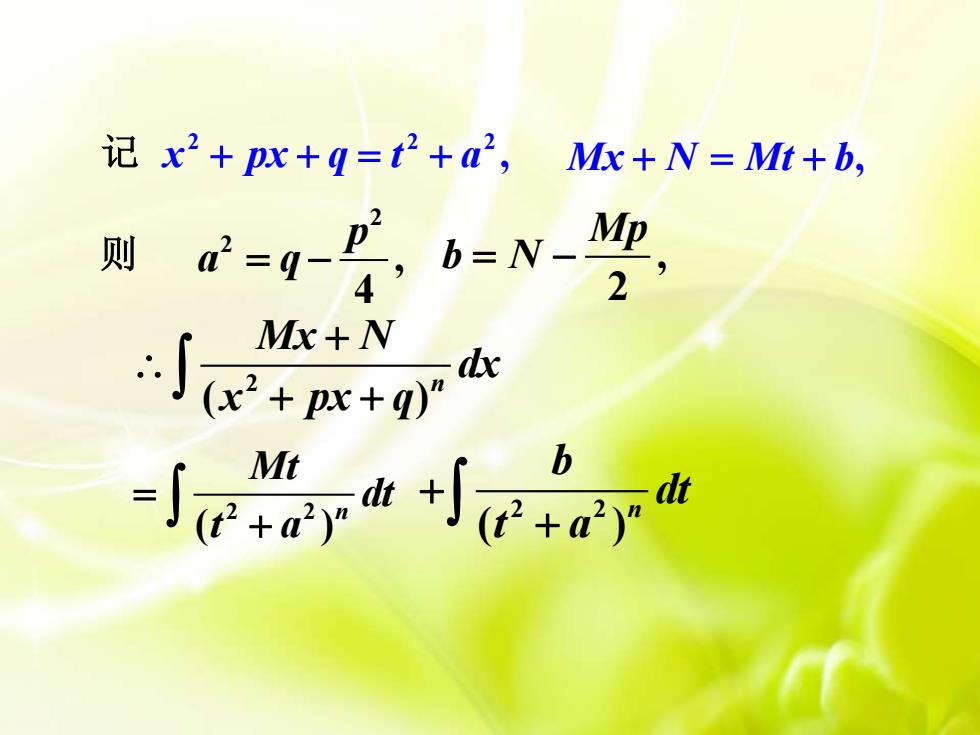
记 x2+px+q=t2+a’,Mx + N = Mt + b.Mpp则 α2=-b=N24Mx + Ndx(x? + px + q)bMtdtdt +2+a")"(t?+a')"(t
2 2 , 4p a q = − , 2 Mp 则 b N = − 2 ( ) n Mx N dx x px q + + + 2 2 ( ) n Mt dt t a = + 2 2 ( ) n b dt t a + + , 2 2 2 记 x + px + q = t + a Mx + N = Mt + b