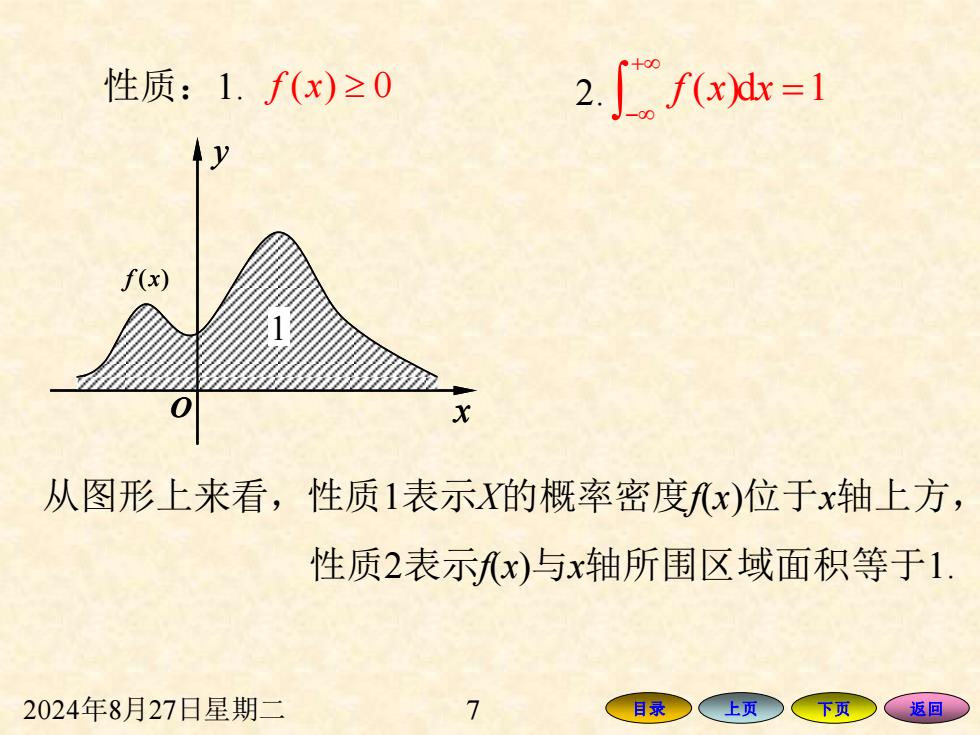
性质:1.f(x)≥0 2.∫f(x=1 f(x 从图形上来看,性质1表示X的概率密度fx)位于x轴上方, 性质2表示x)与x轴所围区域面积等于1 2024年8月27日星期二 7 目录 上页 下页 返回
2024年8月27日星期二 7 目录 上页 下页 返回 性质:1. f x( ) 0 2. ( )d 1 + − = f x x O x y 1 f x( ) 1 O x y 1 f x( ) 1 从图形上来看,性质1表示X的概率密度f(x)位于x轴上方, 性质2表示f(x)与x轴所围区域面积等于1
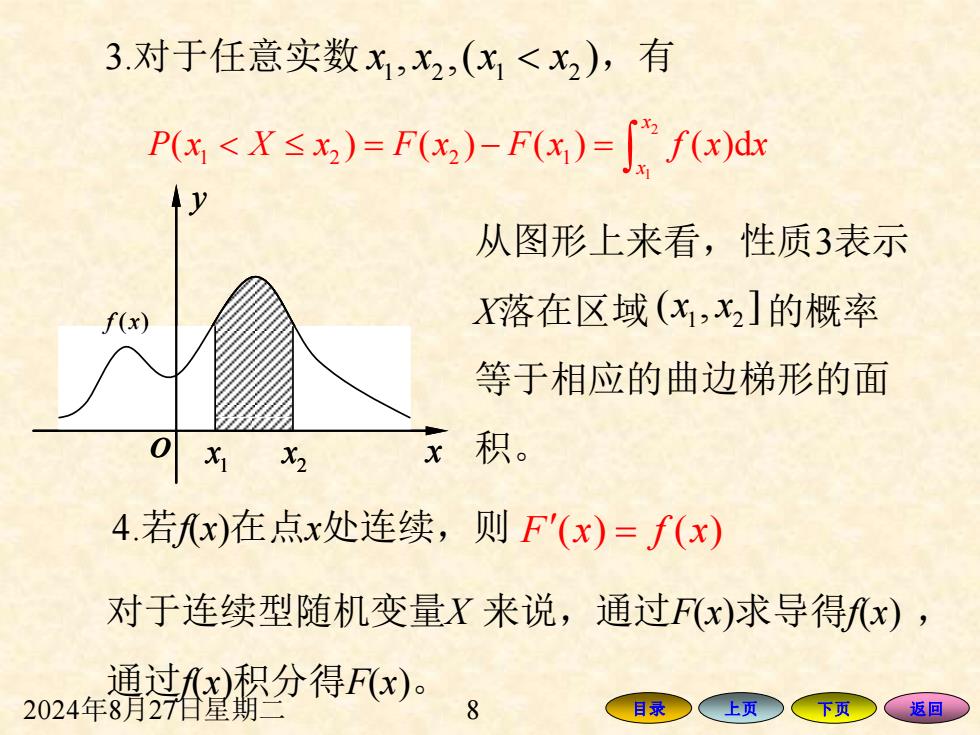
3.对于任意实数x,x2,(x<x2),有 Px<X≤x)=F(x)F(x)=∫fx)d 从图形上来看,性质3表示 f(x) 落在区域(x,x2]的概率 等于相应的曲边梯形的面 x积。 4.若x)在点x处连续,则F'(x)=f(x) 对于连续型随机变量X来说,通过Fx)求导得x), 通过x积分得F(x)。 2024年8月27日星期 目录 上页 下页 返回
2024年8月27日星期二 8 目录 上页 下页 返回 3.对于任意实数 x x x x 1 2 1 2 , ,( ) ,有 2 1 1 2 2 1 ( ) ( ) ( ) ( )d = − = x x P x X x F x F x f x x O x y 1 f x( ) 1 x 2 O x x y 1 f x( ) 1 x 2 x 从图形上来看,性质3表示 X落在区域 的概率 等于相应的曲边梯形的面 积。 1 2 ( , ] x x 4.若f(x)在点x处连续,则 F x f x ( ) ( ) = 对于连续型随机变量X 来说,通过F(x)求导得f(x) , 通过f(x)积分得F(x)

5.连续型随机变量取任一指定实数值的概率为零. 即 P{X=x}=0 由性质5,易得: P(x<X≤x2)=P(x≤X≤x)=P(x<X<x2) =Px≤X<x)=∫fx)d 注:对离散型随机变量,上式不成立。 2024年8月27日星期二 9 目录○ (上页 下页 返回
2024年8月27日星期二 9 目录 上页 下页 返回 5.连续型随机变量取任一指定实数值的概率为零. 即 P X x = = 0 0 由性质5,易得: 1 2 1 2 1 2 P x X x P x X x P x X x ( ) ( ) ( ) = = 2 1 1 2 = = ( ) ( )d x x P x X x f x x 注:对离散型随机变量,上式不成立

第三章多推随机变量及其分市 一维随机变量及其分布 多维随机变量及其分布 2024年8月27日星期二 10 目录 上页>下页○ 返回
2024年8月27日星期二 10 目录 上页 下页 返回 第三章 多维随机变量及其分布 一维随机变量及其分布 多维随机变量及其分布

第一节形雅随机变量及其分布 在实际问题中,对于某些随机试验的结果往往需要同 时用两个或两个以上的随机变量来描述。例如: 试验E:抽样调查15-18岁青少年的身高X与体重Y,以研究当前 该年龄段青少年的身体发育情况。 此时需要研究的不仅仅是X及Y各自的性质,更需要 了解这两个随机变量的相互依赖和制关系。因此,将 二者作为一个整体来进行研究,记为X,)。称X,)为 二维随机变量。 2024年8月27日星期二 11 目录 上页 下页 返回
2024年8月27日星期二 11 目录 上页 下页 返回 第一节 n维随机变量及其分布 在实际问题中,对于某些随机试验的结果往往需要同 时用两个或两个以上的随机变量来描述。例如: 试验E:抽样调查15-18岁青少年的身高X与体重 Y,以研究当前 该年龄段青少年的身体发育情况。 此时需要研究的不仅仅是X及Y各自的性质,更需要 了解这两个随机变量的相互依赖和制约关系。因此,将 二者作为一个整体来进行研究,记为(X, Y)。称(X, Y)为 二维随机变量