
i(0) i(x) i0=i2 i(0) 0(x) 00=02 0 x x' 0 令x'=l-x,x'为传输线上一点到终的距离 0()=20+zie+0-Zi,ex 2 =2+i,e-i,em i(x'=,0 U(x)=U,chyx'+ZcI,shy x :shyxchy i(x)=Zc
令x = l − x,x为传输线上一点到终点的距离 x C x C x C x C I e ZU I e ZU I x U x U Z I e U Z I e − − = + − − = + + − ( ) 21 ( ) 21 ( ) ( ) 21 ( ) 21 ( ) 2 2 2 22 2 2 2 I(0) I(x) U(0) U(x) +- +- 0 x 2 I ( l ) I = 2 U ( l ) = U +-l x x' l x' 0 = + = + x I x ZU I x U x U x Z I x C C ( ) s h ch ( ) ch s h 1 22 2

例 已知一均匀传输线Z=0.427∠79°2/km, Yo=2.7×10-6∠90S/km,02=220kV,i2=455A 频率仁50Hz。求距终端900km处的电压和电流。 解 U(x)=Uchyx'+ZcIshy x' )-Ushy+i.chyx i(x)=Zc Zc= =3982-5.50 Yo y=VZ,Y。=1.073×10-3∠84.5°1/km x'=900km时,yx'=965.7×10-3∠84.5
解 = = − 398 5.5 0 0 Y Z ZC 例 已知一均匀传输线 Z0=0.42779/km , U 2 = 220kV ,I 2 = 455A 频率 f=50Hz。求距终端 900km处的电压和电流。 Y0=2.710-690S/km, 1.073 10 84.5 1/km 3 0 0 = = − Z Y x '= 900km时, 965.7 10 84.5 3 = − x = + = + x I x Z U I x U x U x Z I x C C ( ) s h ch ( ) ch s h 1 2 2 2
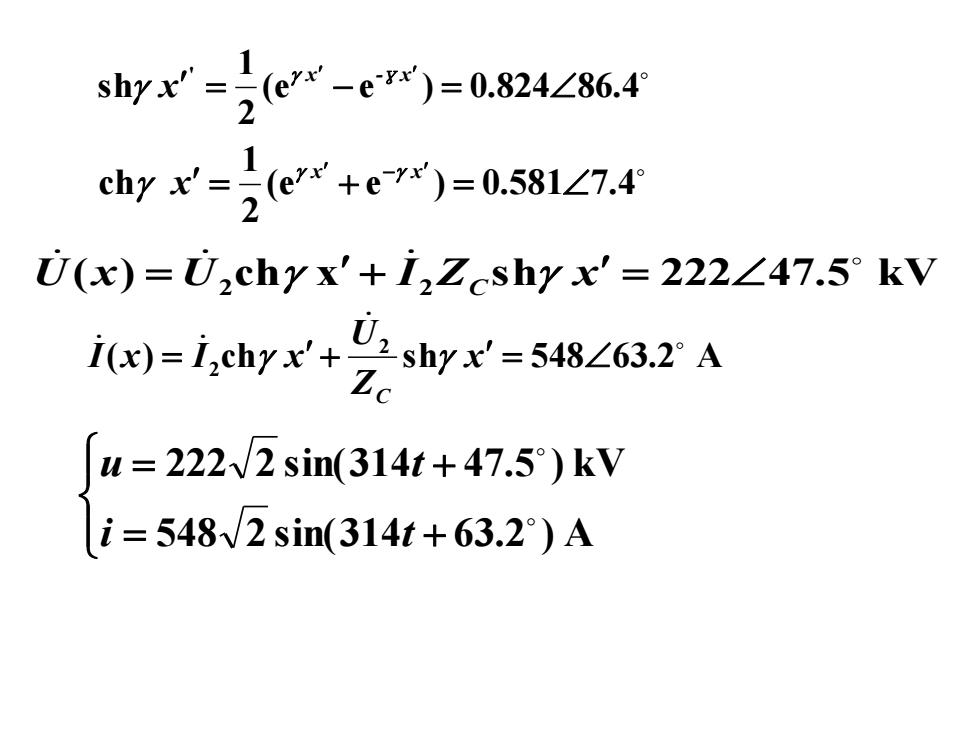
shyx-(c-e)=0.824z86.4 chyx'=,(ex+e)=0.581∠7.4 U(x)=U2chyx'+i2 Zcshyx'=222∠47.5°kV el-i.cy+2sw-5a8∠32A u=222W2sin(314t+47.5)kV i=548W2sin(314t+63.2)A
(e e ) 0.581 7.4 2 1 ch = + = x − x x (e e ) 0.824 86.4 2 1 s h ' = − = x -γ x x ( ) 2 ch x 2 s h 222 47.5 kV U x = U + I ZC x = ( ) ch s h 548 63.2 A 2 2 = + x = Z U I x I x C = + = + 548 2 sin(314 63.2 ) A 222 2 sin(314 47.5 ) kV i t u t

§4均匀传输线上的行波 正弦稳态解为: i= 4e7x- _erx 均匀传输线上的电压,电流可看成由两个分量组成 0=0++0 1=j-r=0+0 Ze Ze
§ 4 均匀传输线上的行波 正弦稳态解为: = − = + − − x C x C x x Z A Z A I U A A e e e e 1 2 1 2 = − = − = + + − + − + − Zc Zc U U I I I U U U 均匀传输线上的电压,电流可看成由两个分量组成 + U − U + I − I

第一项 U+=Aerx 4=io,+z0=4e=44w1 e-rx-e-axe-iox-e-axZ-Bx Ut=A,e7x=Alea∠41-Bx 瞬时值表达式为:wt=√2A1 e-ax sin(ot-Bx+y)
1 1 j 1 1 1 1 1 ( ) e 2 1 A = U + ZC I = A = A x x x x x = = − − − − − e e e e j U A A x x x = = − + − − 1 1 1 e e 第一项 x U A + − = e1 瞬时值表达式为: 2 sin( ) 1 1 = − + + − u A e t x x