
第二项U=A,ex u =2Aeax sin(@t+Bx+y2) 电压u=++ u=2Ae ax sin(@t-Bx+w)+2eax sin(@t+Bx+v2) 电流i=e-。 Zc Zc=ZcLp i=会-Bx+w,-2-so+Ax+yp叭
2 sin( ) 2 2 = + + − u A e t x x 第二项 x U A e = 2 − + − 电压 u = u + u 2 sin( ) 2 sin( ) 1 1 2 2 = − + + + + − u A e t x A e t x x x 电流 2 sin( ) 2 sin( ) 2 2 1 1 = − + − − + + − − e t x Z A e t x Z A i x C x C x C x C Z A Z A I e e 1 2 = − − ZC = ZC
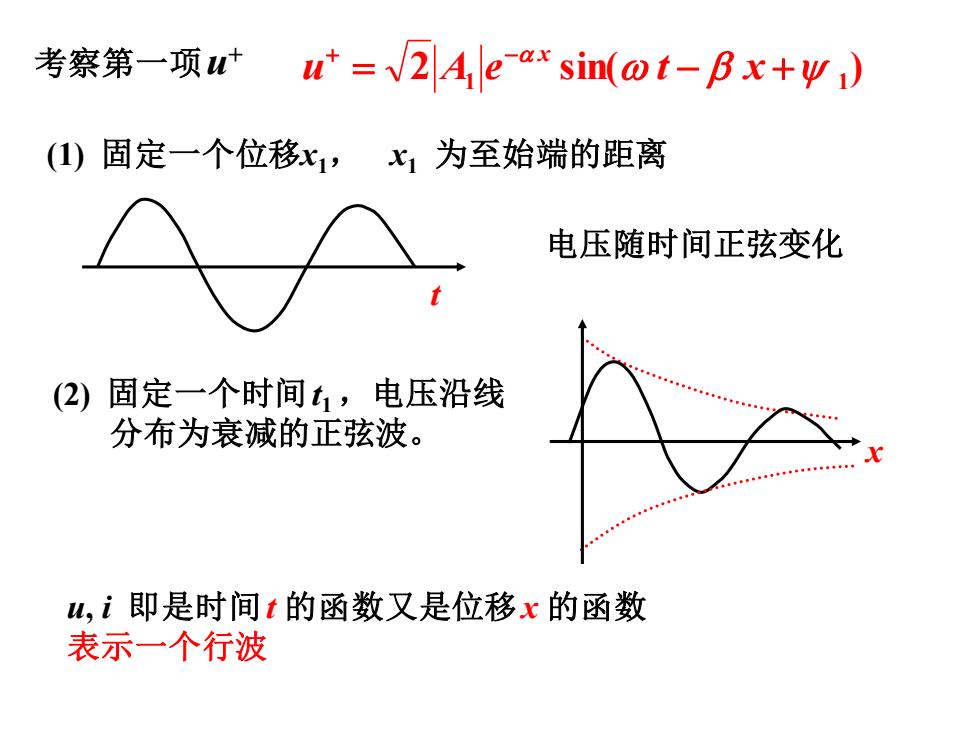
考察第一项t u'=2Ale ax sin(@t-Bx+w) (1)固定一个位移x1,七1为至始端的距离 电压随时间正弦变化 (2)固定一个时间t,电压沿线 分布为衰减的正弦波。 山,i即是时间t的函数又是位移x的函数 表示一个行波
(1) 固定一个位移x1, x1 为至始端的距离 考察第一项u + (2) 固定一个时间t1 ,电压沿线 分布为衰减的正弦波。 x t 电压随时间正弦变化 2 sin( ) 1 1 = − + + − u A e t x x u, i 即是时间t 的函数又是位移x 的函数 表示一个行波

两个问题: 往那移? 速度? 设oa=0ut=V2Asin(ωt-Bx+业i) 选两个同相位的点观察 当t=时,A点在x处。当t=+△t时,A点在x=x+△x处 at1-Bx1+Ψ1(t+△t)-(x1+△x)+Ψ1 结论 波向x增加 的方向移动
两个问题: 往那移? 速度? t = t1 x A x1 选两个同相位的点观察 当 t = t1时,A点在x1处。 1 − x1 + 1 t 结论 波向x增加 的方向移动 A x1+x v 1 1 1 (t + t)− (x + x)+ 当 t = t1+t 时,A点在 x= x1+x 处 2 sin( ) = 1 − + 1 + 设 =0 u A t x
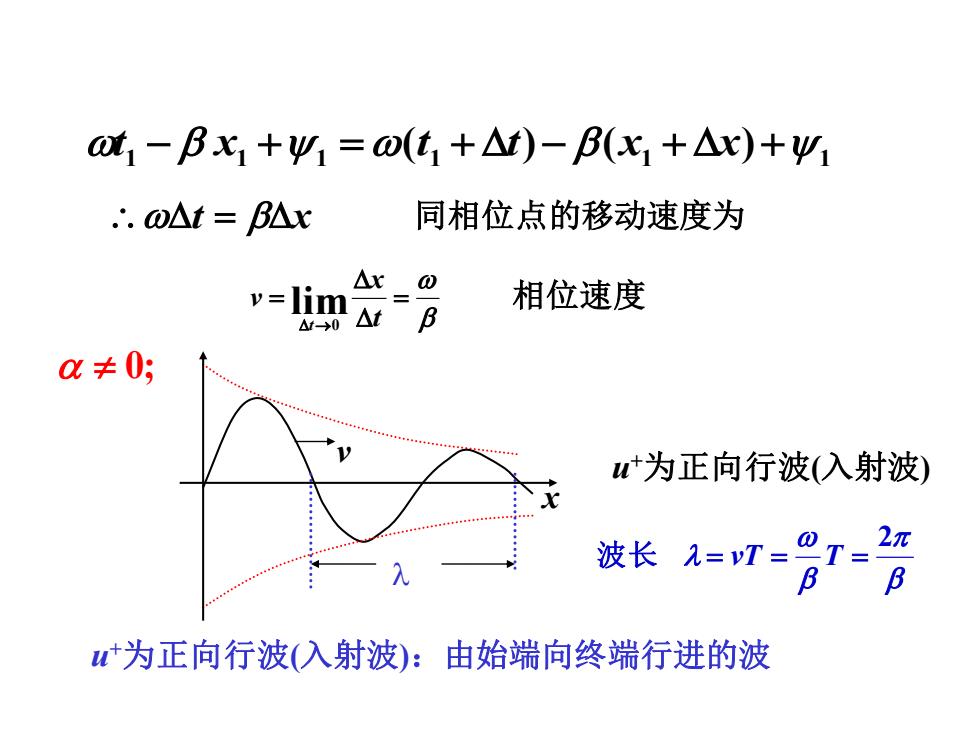
t1-Bx1+y1=o(t1+△t)-B(x1+△x)+y .o△t=BAx 同相位点的移动速度为 y=lim 8 相位速度 △f-0 a≠0; +为正向行波(入射波) 波长九=vT= 0T=2n B B 为正向行波(入射波):由始端向终端行进的波
t = x = = → t x v t lim 0 相位速度 同相位点的移动速度为 1 1 1 1 1 1 t − x + =(t + t)− (x + x)+ 0; x v u +为正向行波(入射波) u +为正向行波(入射波):由始端向终端行进的波 2 波 长 = vT = T =
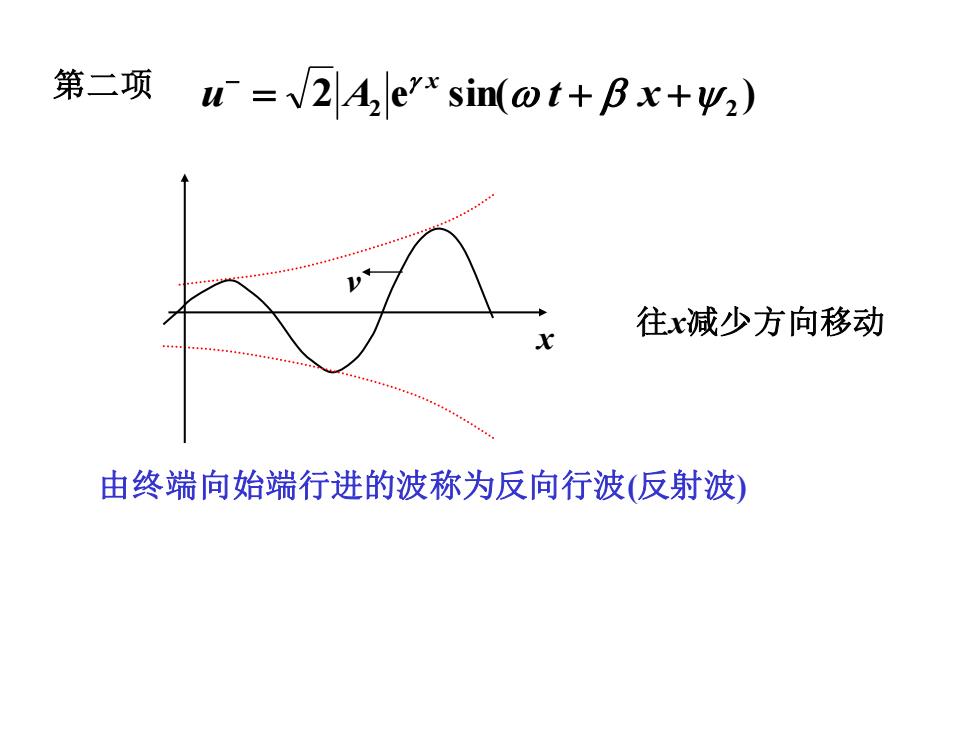
第二项 iu=2Aerx sin(@t+Bx+v2) 往减少方向移动 由终端向始端行进的波称为反向行波(反射波)
第二项 2 e sin( ) 2 2 = + + − u A t x x x v 往x减少方向移动 由终端向始端行进的波称为反向行波(反射波)