f(x) 2.指数分布 3 设连续型随机变量X的概率密度为 x>0 0=1 0=2 2 xs0 其中为常数,则称X服从参数为0的指数分布,记作X~(O), 易知(0fx)20,(2fx)dc=1 F(x) 其分布函数为 8 0=2 F(x)-1-eve x>0 10 04 x≤0 0 0.2 0.1 2345 678910
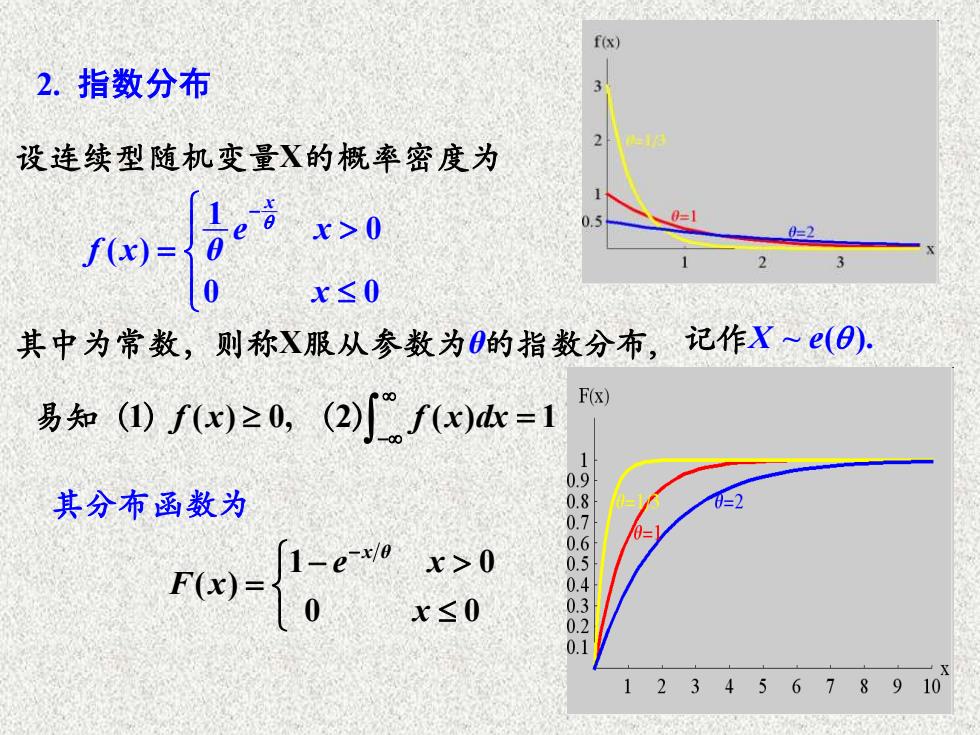
2. 指数分布 其分布函数为 1 0 ( ) 0 0 X X x e x f x θ x θ − = 设连续型随机变量 的概率密度为 其中为常数,则称 服从参数为 的指数分布, 1 ( ) 0, 2 ( ) 1 f x f x dx − = 易知( ) ( ) 1 0 ( ) 0 0 x θ e x F x x − − = 记作X e ~ ( ).

F(x)= 1-e-x/o x>0 指数分布的特性: 0 x≤0 设X服从参数为日的指数分布,对于任意S,t>0,有 P(X>s+t X>s _P{(X>s+tn(X>s)P(X>s+) P(X>s PIX>s sI-F(s+t)e-ostoe 1-F(S) -cm-plX>h. 无记忆性 应用与背景 某些元件、设备或动物的寿命服从指数分布;指数分 布在可靠性理论和排队论中有广泛的应用
P X s t X s { | } + ( ) ( ) { } P X s t X s P X s + = { } { } P X s t P X s + = 1 ( ) 1 ( ) F s t F s − + = − ( )/ / s t s e e − + − = t/ e − = = P X t { }, 应用与背景 指数分布的特性: 某些元件、设备或动物的寿命服从指数分布;指数分 布在可靠性理论和排队论中有广泛的应用。 设X s t 服从参数为的指数分布,对于任意 , 0 ,有 无记忆性 1 0 ( ) 0 0 x θ e x F x x − − =

补例.设某灯管寿命X~e(2000)(单位:小时) (1)任取一灯管,求能正常使用500小时以上的概率 (2)有一只灯管已经正常使用了1000小时以上,求还能使用500 小时以上的概率 解X的概率密度为f(x)=2000 x>0 0 x≤0 dX>5m,-e击在=e=il 1 1 (2)P{X>1500X>1000: =PX>1500,X>500 P{X>1000} P{X>1500}1-P{X≤1500} PX>1000}1-P{X≤1000} 1- 1 =e4≈0.4051
补例. 设某灯管寿命X ~ e(2000)(单位:小时) (1)任取一灯管, 求能正常使用500小时以上的概率. (2) 有一只灯管已经正常使用了1000 小时以上,求还能使用500 小时以上的概率. 解 X 的概率密度为 (1) { 500} P X 1 + 2000 500 1 2000 x e dx − = 1 4 e 0.4051. − = (2) { 1500 1000} P X X { 1500, 500} { 1000} P X X P X = { 1500} { 1000} P X P X = 1 { 1500} 1 { 1000} P X P X − = − 1 1500 2000 0 1 1000 2000 0 1 1 2000 1 1 2000 x x e dx e dx − − − = − 1 4 e 0.4051. − = 1 1 2000 0 ( ) 2000 0 0 t e x f x x − =