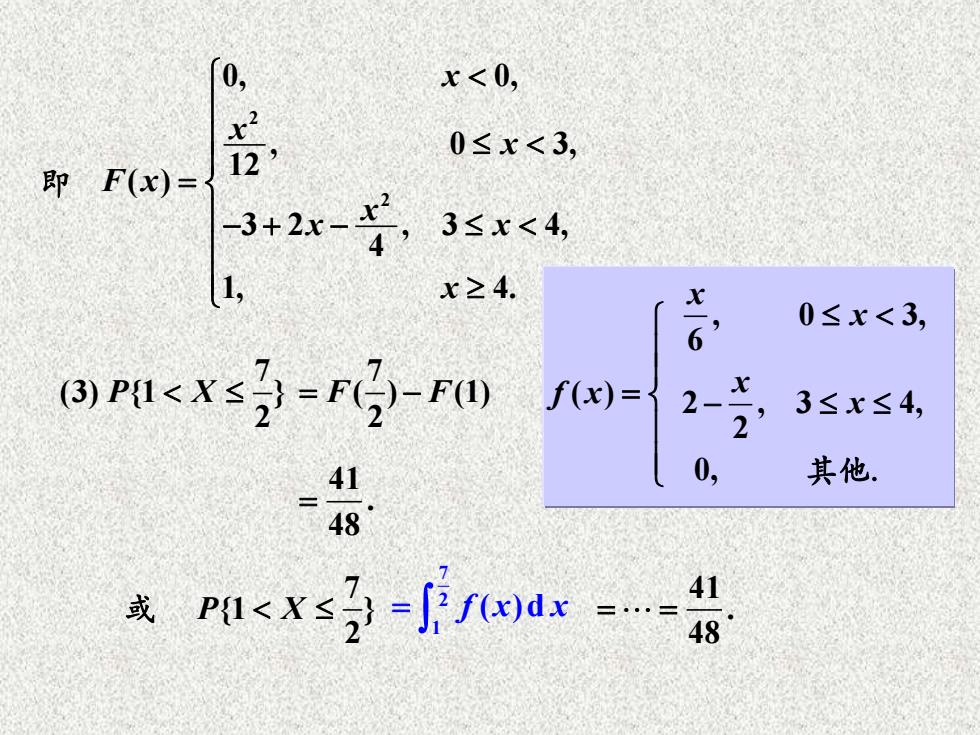
0 x<0, 即F(x)= 12, 0≤x<3, 3+2x- 3≤x<4, x≥4. 0≤x<3, )PI<x≤2-F-F0 f(x)= 2、 3≤x≤4, 41 0, 其他. 48 或 asf fdy
2 2 0, 0, , 0 3, 12 ( ) 3 2 , 3 4, 4 1, 4. x x x F x x x x x = − + − 即 7 (3) {1 } 2 P X 7 ( ) (1) 2 = − F F 41 . 48 = f x( ) = , 0 3, 6 2 , 3 4, 2 0, x x x x − 其他. 7 {1 } 2 或 P X 7 2 1 = f x x ( )d 41 . 48 = =

说明:1)limf(x)=limf(x)=0; 2)P{x1<X≤x2}为相应曲边梯形的面积 3)P{x<X≤x+△r}≈f(x)△x(△x很小) 4)若X为连续型随机变量,则对任一实数, 有P{X=0}=0. >P{a≤X≤b}=P{a<X≤b}=P{a≤X<b} =Pa<X<b}-∫fx)dx 5)概率为0的事件不一定是不可能事件。同样,概率为1的 事件也不一定是必然事件。 若X为离散型随机变量, {X=}是不可能事件台PX=}=0 X的概率密度连续性 X的概率分布~X的分布函数~ X的分布律离散型
3)P x X x x f x x x { } + ( ) ( 很小) 说明: 2 { } )P x X x 1 2 为相应曲边梯形的面积 4)若X 为连续型随机变量,则对任一实数 a, 有 P{X=a}=0. P a X b { } = P a X b { } = P a X b { } ( )d b a = f x x = P a X b { } { } X a = 是不可能事件 = = P X a { } 0. 若 X为离散型随机变量, 5)概率为0的事件不一定是不可能事件。同样,概率为1 的 事件也不一定是必然事件。 1) lim ( ) lim ( ) 0; x x f x f x →− →+ = = X的概率分布 ~ X的分布函数~ X的概率密度——连续性 X的分布律——离散型

二、常见的连续型随机变量 要求:牢记密度函数及 其图像! 1.均匀分布 定义设连续型随机变量X具有概率密度 (x) f()- a<x<b, 0, 其它, 0 则称X在区间(a,b)上服从均匀分布,记作X~U(a,b), 验证: (1).对任意的x,有f(x)≥0; 2-了y=j6是= 说明:若X~U(a,b),则它落在区间(a,b)的子区间内 的概率与子区间长度成正比而与子区间的位置无关
, ~ ( , ). 1 , , ( ) 0, , ( , ) X a x b f x b a X a b X U a b = − 设连续型随机变量 具有概率密度 其它 定 则称 在区间 上服从均匀分 记作 义 布 二、常见的连续型随机变量 1. 均匀分布 ⑴.对任意的x f x ,有 ( ) 0; ( ) 1 1 b a f x dx dx b a + − = = − ⑵. 若X U a b a b ~ ( , , ),则它落在区间( )的子区间内 的概率与子区间长度成正比而与子区间的位 说明: 置无关。 验证: 要求:牢记密度函数及 其图像! o x f (x) a b
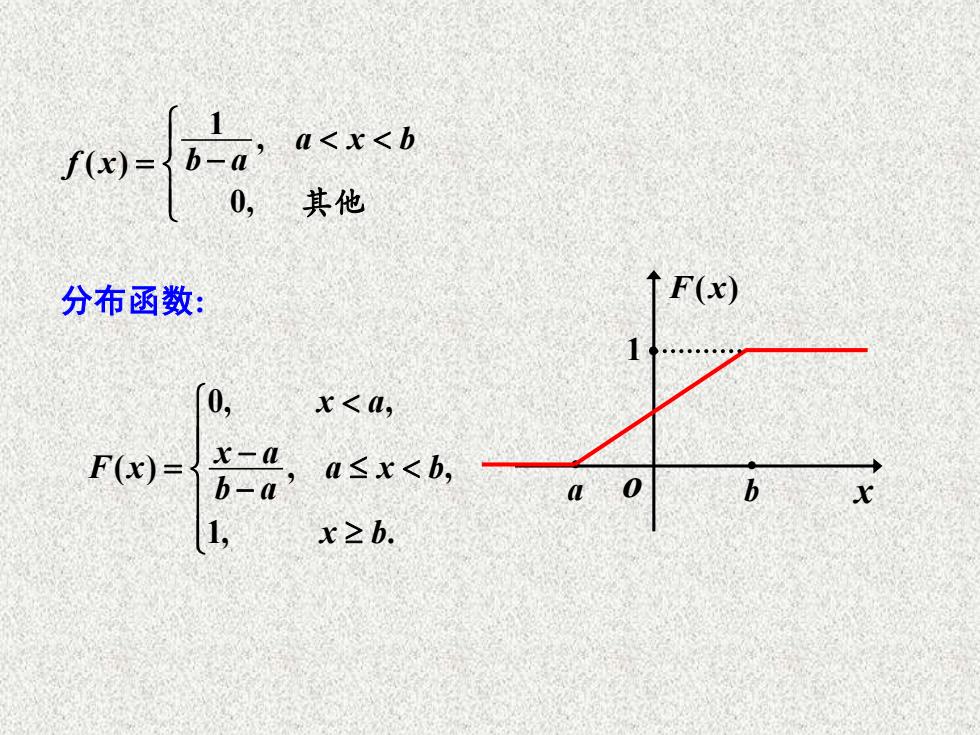
a<x<b 0, 其他 分布函数: IF(x) 0, x<, F()= x-a b-a a≤x<b, 1, x≥b
a • 0, , ( ) , , 1, . x a x a F x a x b b a x b − = 分布函数: o x F x( ) b • 1 1 , ( ) 0, a x b f x b a = − 其他

例2设电阻值R是一个随机变量,均匀分布在900欧~1100欧. 求R的概率密度及R落在950欧~1050欧的概率. 解由题意,R~U(900,1100) o- /(1100-900), 900<r<1100, , 其他。 900<r<1100, o, 其他. 故有 050)00d0.5
例2 设电阻值R是一个随机变量,均匀分布在900欧~1100欧. 求R的概率密度及R 落在950欧~1050欧的概率. 解 由题意,R ~U(900,1100) 1 (1100 900), 900 1100, ( ) 0, . r f r − = 其他 故有 P R 950 1050 1050 950 1 d 0.5. 200 = = r 1 , 900 1100, 200 0, . r = 其他