
第十节闭区间上连续函数的性质 二、零点定理与介值定理 定义如果使fco)=0,则称x为函数fw)的 零点. 定理2(零点定理)设函数fx)在闭区间[,b]上连 续,且f(@与fb)异号(即f(@)·fb)<0),那么在开 区间(a,)内至少存在一点5,使 f(5)=0. 上页 下页 返回 MathGS 公式 线与面 数学家
第十节 闭区间上连续函数的性质 二、零点定理与介值定理 定义 如果 x0 使 f (x0 ) = 0,则称 x0 为函数 f (x) 的 零点. 定理2(零点定理) 设函数 f (x) 在闭区间 [a , b] 上连 续,且 f (a) 与 f (b) 异号 (即 f (a) f (b) < 0),那么在开 区间 (a , b) 内至少存在一点 ,使 f ( ) = 0
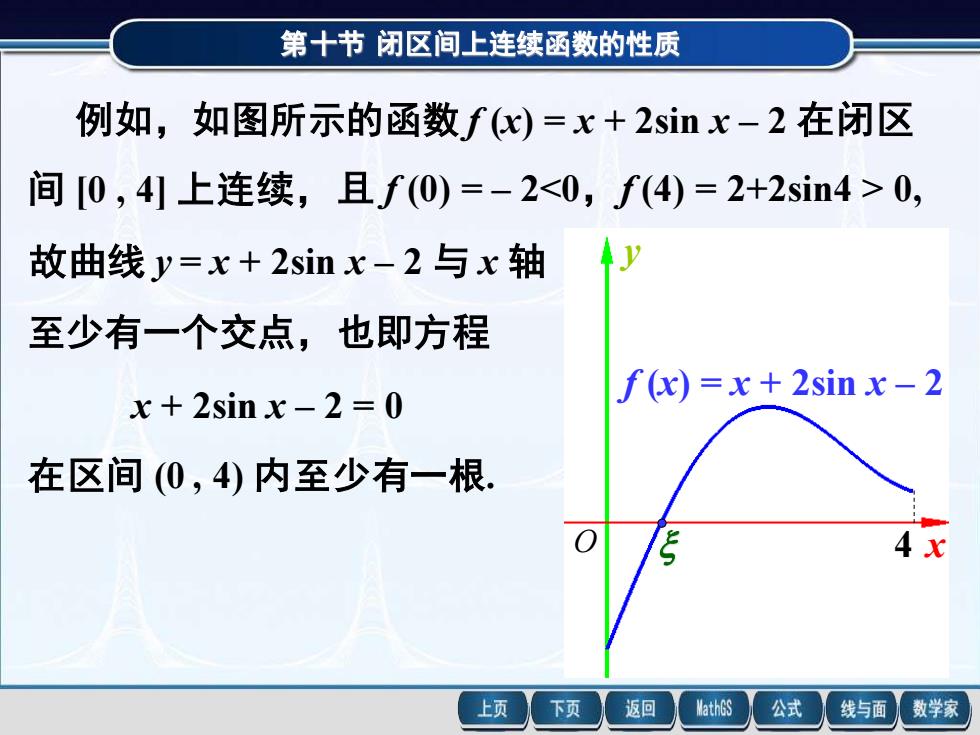
第十节闭区间上连续函数的性质 例如,如图所示的函数f(x)=x+2sinx-2在闭区 间[0,4上连续,且f(0)=-2<0,f(4)=2+2sin4>0, 故曲线y=x+2sinx-2与x轴 至少有一个交点,也即方程 x+2sin x-2=0 f(x)=x+2sin x-2 在区间(0,4)内至少有一根, 4x 上页 下页 返回 MathGS 公式 线与面 数学家
第十节 闭区间上连续函数的性质 例如,如图所示的函数 f (x) = x + 2sin x – 2 在闭区 间 [0 , 4] 上连续,且 f (0) = – 2<0,f (4) = 2+2sin4 > 0, 故曲线 y = x + 2sin x – 2 与 x 轴 至少有一个交点,也即方程 x + 2sin x – 2 = 0 在区间 (0 , 4) 内至少有一根. x y O f (x) = x + 2sin x – 2 4