
.4.第一章复数与复变函数(2+2),Im2=1(2 —2).Rez=2i1例1.1设21,22是任意两个复数,求证:2Re(2122) = 2:22 + 2122.(2+2)可算得证利用公式Re222Re(2122)=2)22+(2122)=222+2232+2122学习了以上两段以后,读者可仔细体会,以加深对复数的认识,最初当给出复数概念时,我们所知道的复数是什么?复数无非是一个实数同另一个实数用""及“+”连接而写成"十i”这样一个形式的东西,“”是什么,“十”是什么意思,都未加说明.后来,介绍了复数与实数的关系,复数与纯虚数的关系,又介绍了复数加法的定义,这样,我们也就可以把r十iy看成实数z同纯虚数iy相加.其后,又定义了复数乘法,利用复数的加法与乘法,现在已可将复数&一十i真正理解为虚数i乘y,然后再加上r的结果(注意r=r+i0,y=y+i0,i=0+1i):z=(+Oi)+(0+1i)(y+0i)-r+iy历史上,当人们第一次引进1的平方根并把它当作“数”的时候,是把它作为想像中的数,所以称为“虚数”后来就把形如,十iy的数叫做复数,意思是“复合”起来的数,81.1.3复平面一个复数十iy可唯一地对应一个有序实数对(r,y).而有序实数对与坐标yi平面上的点是一一对应的.所以,复数2xtiy全体与坐标平面上的点的全体形成一对应。现在我们直截了当地把坐标平面上0的点写成十iy(图1.1),那么,横轴上的点就表示实数·纵轴上的点就表示纯虑图1.1数.整个坐标平面可称为复(数)平面:今

31.2复数的三角表示后我们索性将复数与复平面的点不加区分,这种点,数等同将给我们带来许多方便,在点、数等同的观点下,一个复数集合就是一个平面点集,因此,很自然地.某些特殊的平面点集就可以用复数所满足的某种关系式来表示,例如、izIm0!与z:0<Re21.0≤im2≤1分别表示上半平面与以0,1.1+i.i为顶点的正方形81.2复数的三角表示81.2.1复数的模与辐角上面说过,复数与平面上的点作成一一·对应,这是将复数实部与虚部分别看作直角坐标系下点的横坐标与纵坐标.除此以外.复数还可以同平面向量作成对应,只要将复数的实部与L虚部分别看作向量的水平分量与铅垂分量就行了.所以我们也可以把复数与平面向量等x+iy同起来.不过要注意,向量其有平移不变性即其起点可安放在任意·一点,如果把向量的起点放在(复乎面的)坐标原点,则此向量及向量的终点在上述两种对应下恰好对应同一。图 1. 2 个复数(图1.2).如果是一个不为0的复数,我们把它所对应向量的长度叫做之的模,记作;把它所对应向量的方向角叫做2的辐角,辐角有无穷多个值,其中任意两个值相差2元的整数倍.今后,我们用记号AIg作为之的辐角的一般表示.意思是它可以不受限制地取的辐角的任意值,再用记号arg表示的所有辐角中介于一与之间(包括元)的那--个角,并把它称为≥的主辐角,即一元<arg之元(顺便指出,有的书
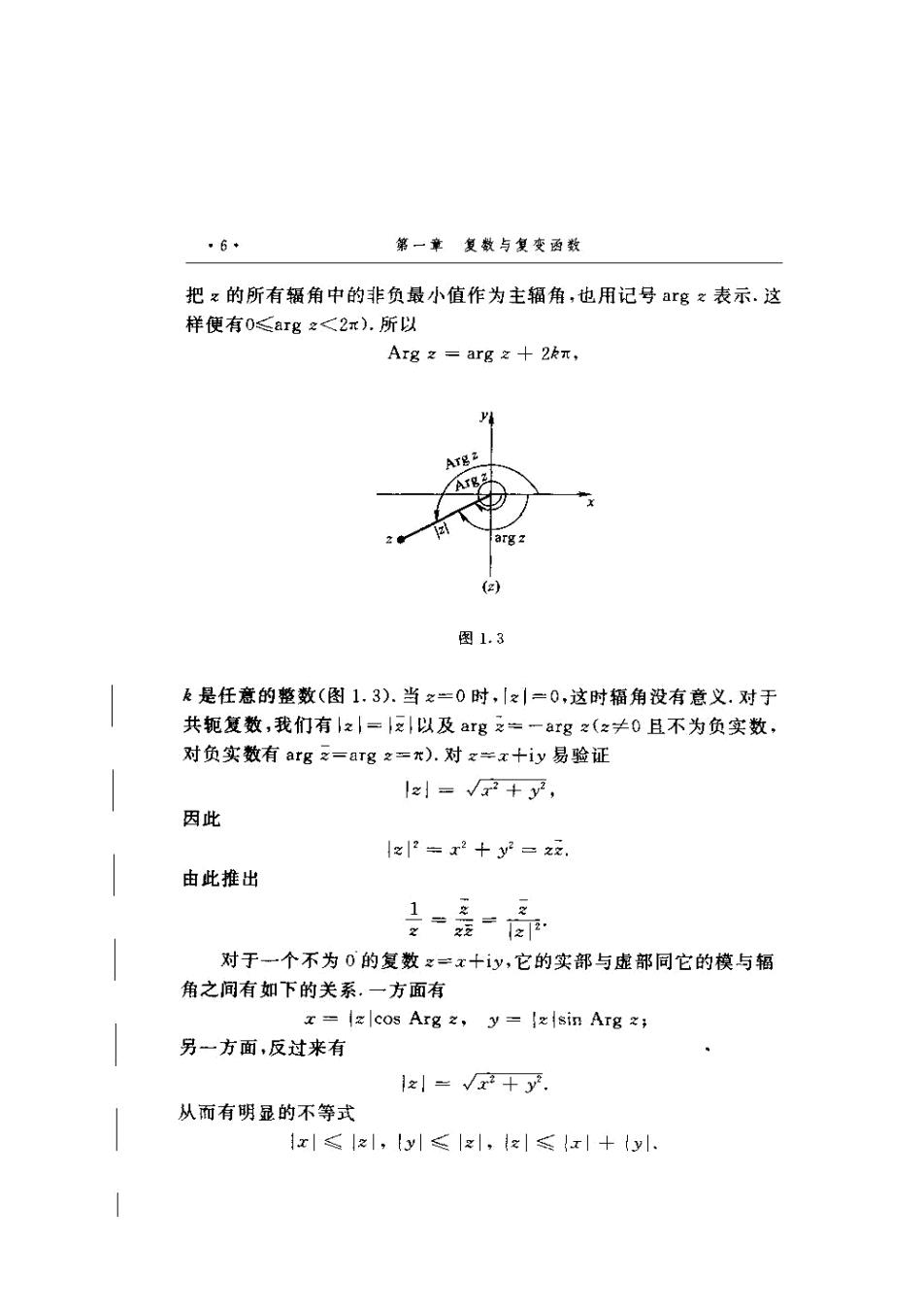
*6+第一章复数与复变函数把之的所有辐角中的非负最小值作为主辐角,也用记号ar之表示,这样便有0<aig2<2元).所以Arg z = arg z+ 2k元,Y4AIg3argz(2)图1.3k是任意的整数(图1.3).当之=0时,2|=0,这时辐角没有意义.对于共轭复数,我们有1|以及arg一arg(2≠0且不为负实数,对负实数有arg=arg=).对=十iy易验证=V+因此[212 = 2 + 32 = zz.由此推出1-22对于一个不为0的复数=十iy,它的实部与虚部同它的模与辐角之间有如下的关系,一方面有=-izlcos Arg 2,y=lisin Arg 2;另一方面,反过来有12l=V+y.从而有明显的不等式Iα/≤z/, (y/≤[z],(z/≤+(y]
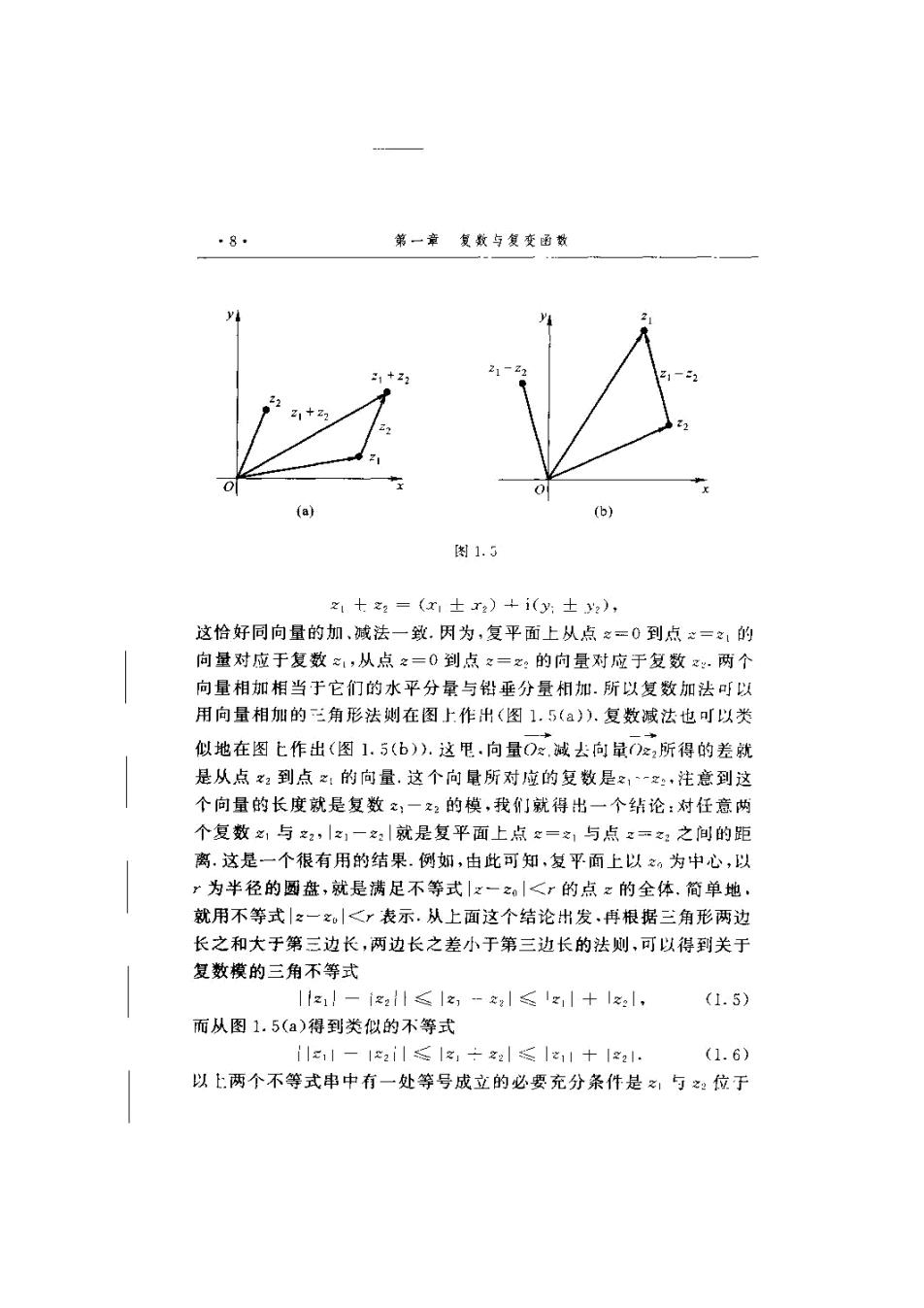
第一章-8.复数与复变函数.2Jo-(a)(b)图1. 52 + z2 =(r ±r2) +i(y ± ),这恰好同向量的加、减法一致,因为,复平面上从点一0到点=的向量对应于复数从点之=0到点2一的向量对应于复数两个向量相加相当于它们的水平分量与铅垂分量相加.所以复数加法可以用向量相加的三角形法则在图上作出(图1.5(a)).复数减法也可以类似地在图七作出(图1.5(b)).这甩向量0减去向量()22所得的差就是从点22到点2,的向量,这个向量所对应的复数是21-2:,注意到这个向量的长度就是复数,一22的模,我们就得出一个结论:对任意两个复数与2,121—21就是复平面上点=与点=之间的距离.这是一个很有用的结果,例如,由此可知,复平面上以,为中心,以为半径的圆盘,就是满足不等式一2<r的点的全体,简单地,就用不等式|2一2<r表示.从上面这个结论出发.再根据三角形两边长之和大于第三边长,两边长之差小于第三边长的法则,可以得到关于复数模的三角不等式z/122/≤z-2/≤12+ 1z1,(1.5)而从图1.5(a)得到类似的不等式二2—22-【12-十22——2=+22](1. 6)以E两个不等式串中有一处等号成立的必要充分条件是与位于