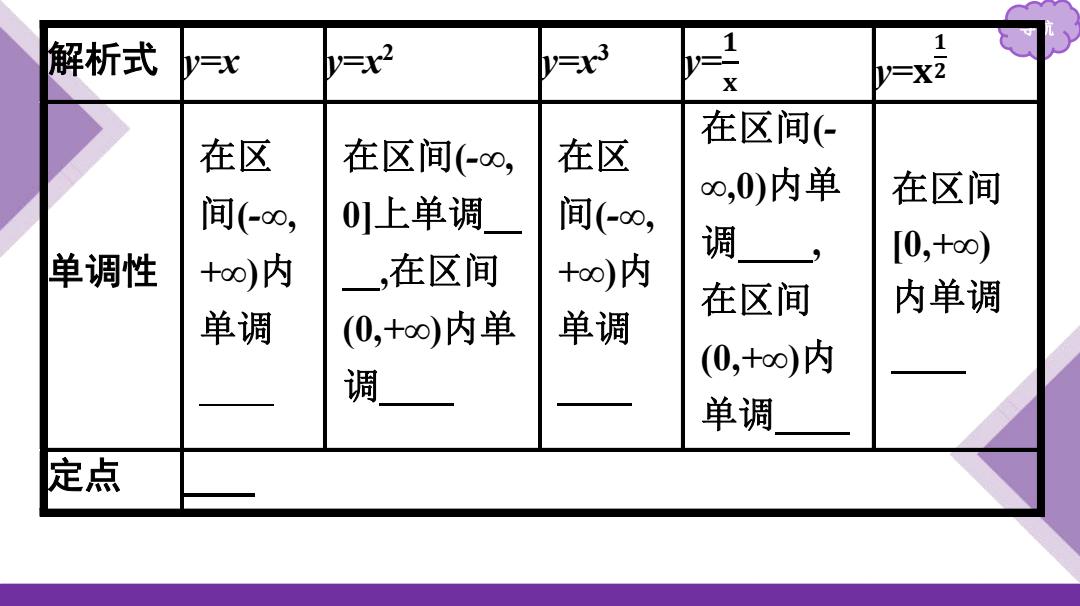
解析式 1 y=x y=x2 =x3 X =X2 在区间( 在区 在区间(-0, 在区 00,0)内单 在区间 间(-o0, 0]上单调 间(-o0, 调 [0,+oo) 单调性 +oo)内 ,在区间 +o)内 在区间 内单调 单调 (0,+o∞)内单 单调 (0,+o)内 调 单调 定点
导航 解析式 y=x y=x2 y=x3 y= 𝟏 𝐱 y=𝐱 𝟏 𝟐 单调性 在区 间(-∞, +∞)内 单调 递增 在区间(-∞, 0]上单调递 减,在区间 (0,+∞)内单 调递增 在区 间(-∞, +∞)内 单调 递增 在区间(- ∞,0)内单 调递减, 在区间 (0,+∞)内 单调递减 在区间 [0,+∞) 内单调 递增 定点 (1,1)

(2)幂函数y=x的性质 ①所有的幂函数在区间(0,+∞)内都有定义,因此在第一象限内 都有图象,并且图象都通过点 ②如果>0,则幂函数的图象通过 ,且在区间[0,+oo)内是 函数. ③如果a<0,则幂函数在区间(0,+∞)内是减函数,且在第一象限 内:当x从右边趋向于原点时,图象在y轴右方且无限地逼近y轴; 当x无限增大时,图象在x轴上方且无限地逼近x轴
导航 (2)幂函数y=xα的性质 ①所有的幂函数在区间(0,+∞)内都有定义,因此在第一象限内 都有图象,并且图象都通过点(1,1). ②如果α>0,则幂函数的图象通过原点,且在区间[0,+∞)内是增 函数. ③如果α<0,则幂函数在区间(0,+∞)内是减函数,且在第一象限 内:当x从右边趋向于原点时,图象在y轴右方且无限地逼近y轴; 当x无限增大时,图象在x轴上方且无限地逼近x轴