
由X,~N(0,1)知,X~x2(I)(i=1,2,.,n).不难证明, X分布具有下列性质: (1)x2分布的数学期望和方差:若x2~x2(n),则有 Ex2=n,Dx2=2n. (2)x2分布的可加性:设~X2(n),3~x2(n2),且 ,好相互独立,则有 +3~X2(n+h2). 推广若X,X2,.,X相互独立,且X,~X(n,), i=1,2,.,k,则 立x-x2n) 2024年8月27日星期二 目录 长上页 下页 返回
2024年8月27日星期二 7 目录 上页 下页 返回 由 ~ (0,1) X N i 知, 2 2 ~ (1) Xi ( 1, 2, , ) i n = .不难证明, 2 分布具有下列性质: (1) 2 分布的数学期望和方差: 若 2 2 ~ ( ) n ,则有 2 E n = , 2 D n = 2 . (2) 2 分布的可加性:设 2 2 1 1 ~ ( ) n , 2 2 2 2 ~ ( ) n ,且 2 1 , 2 2 相互独立,则有 2 2 2 1 2 1 2 + + ~ ( ) n n . 推广 若 1 2 , , , X X Xk 相互独立, 且 2 ~ ( ) X n i i , i k =1,2, , ,则 2 1 1 ~ ( ) k k i i i i X n = = .
(3)x分布的分位数:对于给定的正数α(0<<1), 称满足条件 P{x2>x2(}=∫f(y)dy=a 的点(n)为x(n)分布的上侧a分位数 (upper a-quantile), f) a(n) 2024年8月27日星期二 8 目录 上页 下页 返回
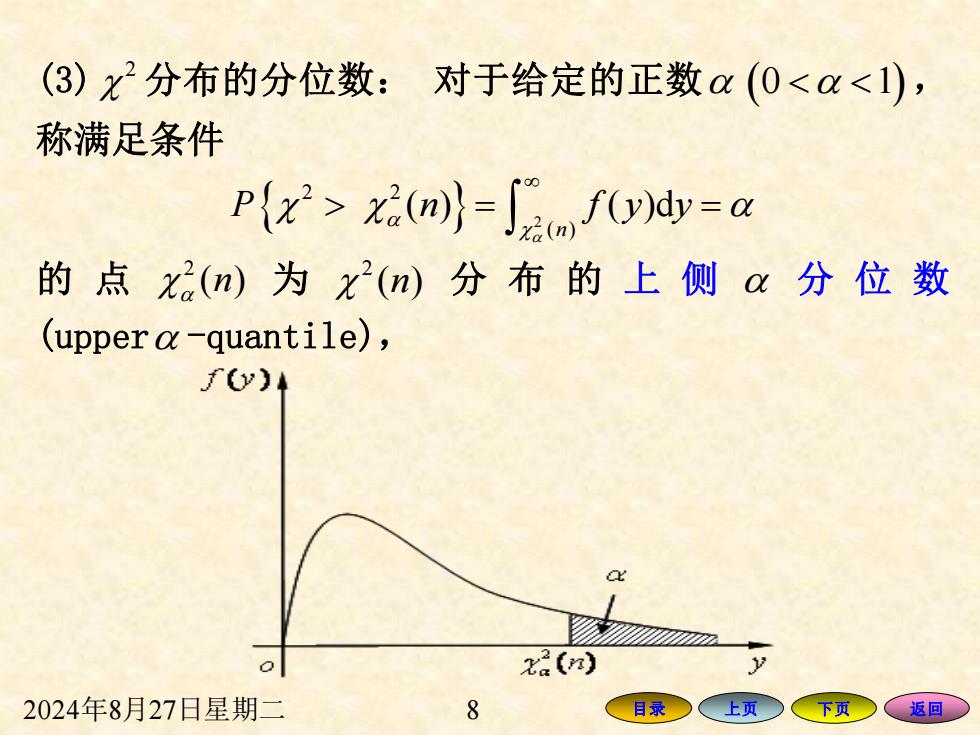
2024年8月27日星期二 8 目录 上页 下页 返回 (3) 2 分布的分位数: 对于给定的正数 (0 1 ) , 称满足条件 2 2 2 ( ) ( ) ( )d n P n f y y = = 的 点 2 ( ) n 为 2 ( ) n 分 布 的 上 侧 分 位 数 (upper -quantile)

二、t分布 定义5设X~N(0,1),Y~x2(nm)且X与Y相互独立,则 称随机变量T= X 服从自由度为n的t分布,记为 √7 I~t(n). t分布又称为学生氏分布(student distribution).t(n) 分布的概率密度函数为 n+l 1(2 2 f(t)= ,-00<t<0. 2024年8月27日星期二 目录○ 上页 下页 返回」
2024年8月27日星期二 9 目录 上页 下页 返回 二、t分布 定义 5 设 X N~ (0,1), 2 Y n ~ ( ) 且 X 与 Y 相互独立,则 称随机变量 / X T Y n = 服从自由度为 n 的 t 分布,记为 T t n ~ ( ) . t 分布又称为学生氏分布(student distribution).t n( ) 分布的概率密度函数为 1 2 2 1 2 ( ) 1 π 2 n n t f t n n n + − + = + ,− t .
其图形为 J() W(0,1) t10) t(2) f(t)的图形关于t=0对称,当n充分大时,t分布接近标 准正态分布,因此在应用中,当n>45时,有ta(n)≈2a· 2024年8月27日星期二 10 目录○ 上页 下页 返回>
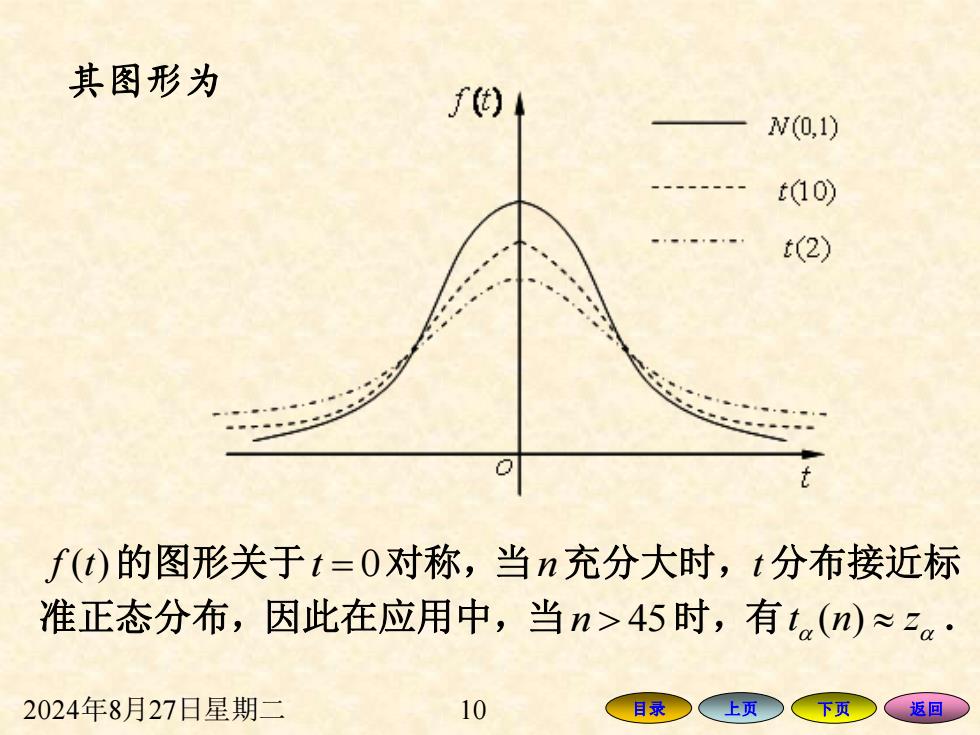
2024年8月27日星期二 10 目录 上页 下页 返回 其图形为 f t( )的图形关于t = 0对称,当n充分大时,t 分布接近标 准正态分布,因此在应用中,当n 45时,有t n z ( ) .