
第四章 随机变量的数字特征
第四章 随机变量的数字特征
引例1某大型体育赛事需要对甲、乙两名射击选 手进行选拔。参赛组委会对两名选手分别测试了 100次,下面是选拔测试中他们的命中环数的成绩: 甲命中环数 乙命中环数 8 10 8 9 10 (X) (Y) 次数 30 25 45 次数 16 50 34 甲射中的平均环数: 8×30+9×25+10×45 = 8×0.3+9×0.25+10×0.45=9.15(环) 100 乙射中的平均环数: 8×16+9×50+10×34 =8×0.16+9×0.5+10×0.34=9.18(环) 100 故从射中的平均环数比较,乙的技术优于甲
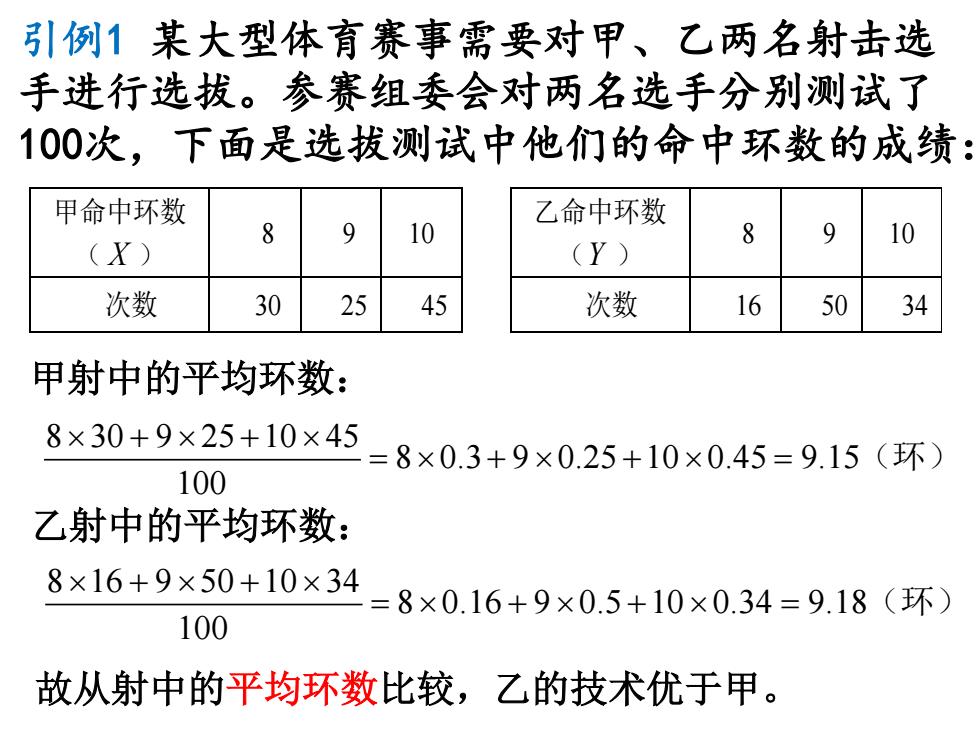
引例1 某大型体育赛事需要对甲、乙两名射击选 手进行选拔。参赛组委会对两名选手分别测试了 100次,下面是选拔测试中他们的命中环数的成绩: 甲命中环数 ( X ) 8 9 10 次数 30 25 45 乙命中环数 (Y ) 8 9 10 次数 16 50 34 甲射中的平均环数: 8 30 9 25 10 45 8 0.3 9 0.25 10 0.45 9.15 100 × +× + × =× +× + × = (环) 乙射中的平均环数: 8 16 9 50 10 34 8 0.16 9 0.5 10 0.34 9.18 100 × +× + × =× +× + × = (环) 故从射中的平均环数比较,乙的技术优于甲
引例2假设两个风险资产的收益X,Y都服从正 态分布(而事务界也常常用正态分布估计风险资 产的收益),假设两个资产收益率分布具体为: X≈N(8,4) Y~N(8,9) (单位:百分比)。投资者对这两个资产该做什 么决策?其依据是什么? 0.2 N(8,9) 0.15 N(8.4) 0.1 0.05 0 8 10 15 20
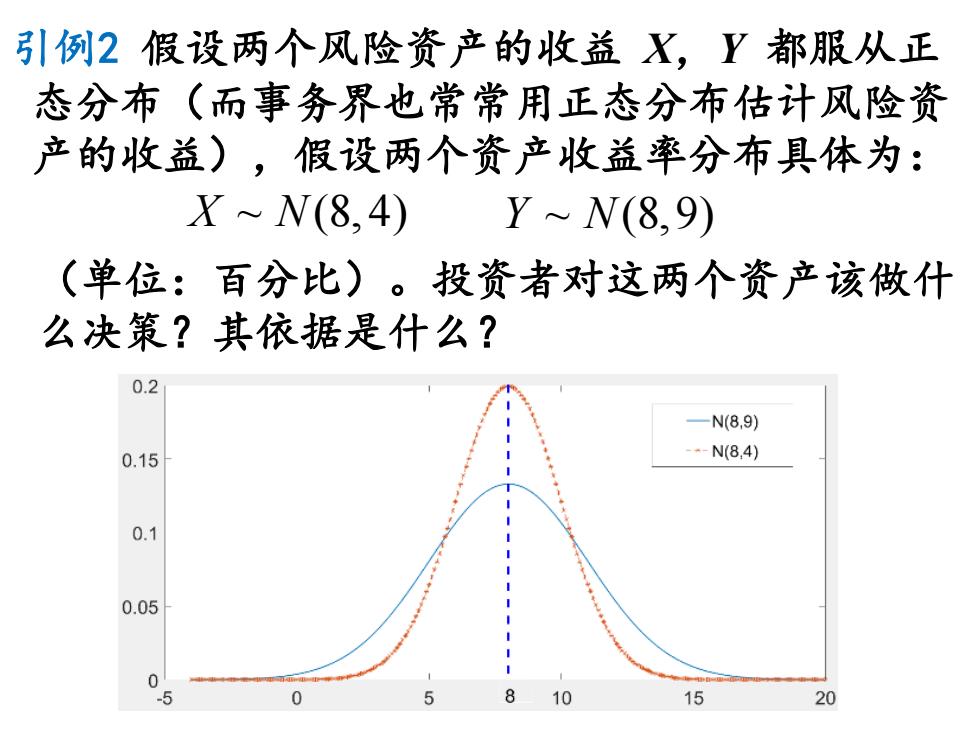
引例2 假设两个风险资产的收益 X,Y 都服从正 态分布(而事务界也常常用正态分布估计风险资 产的收益),假设两个资产收益率分布具体为: X N ~ (8, 4) Y N ~ (8,9) (单位:百分比)。投资者对这两个资产该做什 么决策?其依据是什么?

随机变量的平均取值一数学 本章内容 期望 随机变量取值平均偏离平均值的 情况一 方差 描述两个随机变量之间的某种关 系的数一 协方差与相关系数
随机变量的平均取值 —— 数学 期望 随机变量取值平均偏离平均值的 情况 —— 方差 描述两个随机变量之间的某种关 系的数 —— 协方差与相关系数 本 章 内 容

4.1数学期望 定义1离散型随机变量的数学期望 设离散型随机变量X的分布律为 P(X=x)=p,k=1,2,… 若无穷级数 XkPk k=1 绝对收敛,则称其和为随机变量X的数学期望 记为 EX=∑xP k=1
设离散型随机变量X 的分布律为 ( ) , 1,2, PX x p k k k = = = 若无穷级数 1 k k k x p +∞ = ∑ 绝对收敛,则称其和为随机变量 X 的数学期望 记为 1 k k k EX x p +∞ = = ∑ 定义1 离散型随机变量的数学期望 4.1 数学期望