5.2中心极限定理 引例 X,X,.., Xm相互 独立,均服从参数为 1.0 1.4 12 2的指数分布,令 0. k=1 0.8 0.7 n=2 n=5 >n=2 n=15 n=20 0.5 -n=30 30.4 n=5 n=15 0.3 n=20 n=30 2. 0 10 15 20 25 30
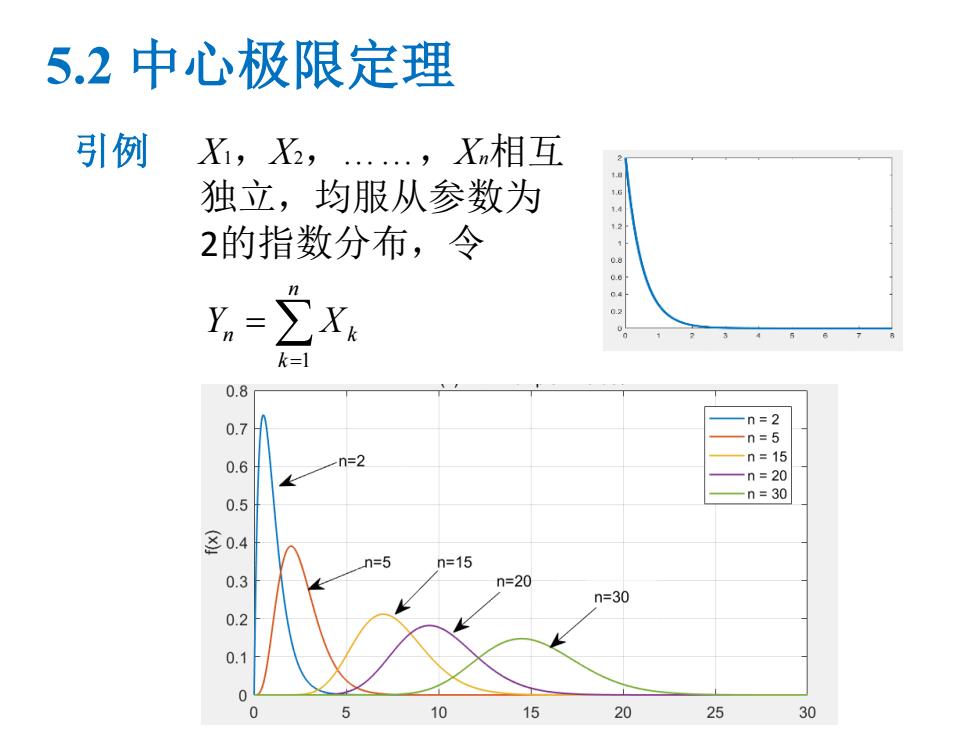
5.2 中心极限定理 引例 X1,X2,……,Xn相互 独立,均服从参数为 2的指数分布,令 1 n n k k Y X = = ∑
n=30 n=2 n=5 n=50 4 n=15 n=20 n=30 83 n=50 0.5 1.5 =12x n k=1 主要分布区域越来越集中,其中心位 置越来越接近 EZ)=}=0,5
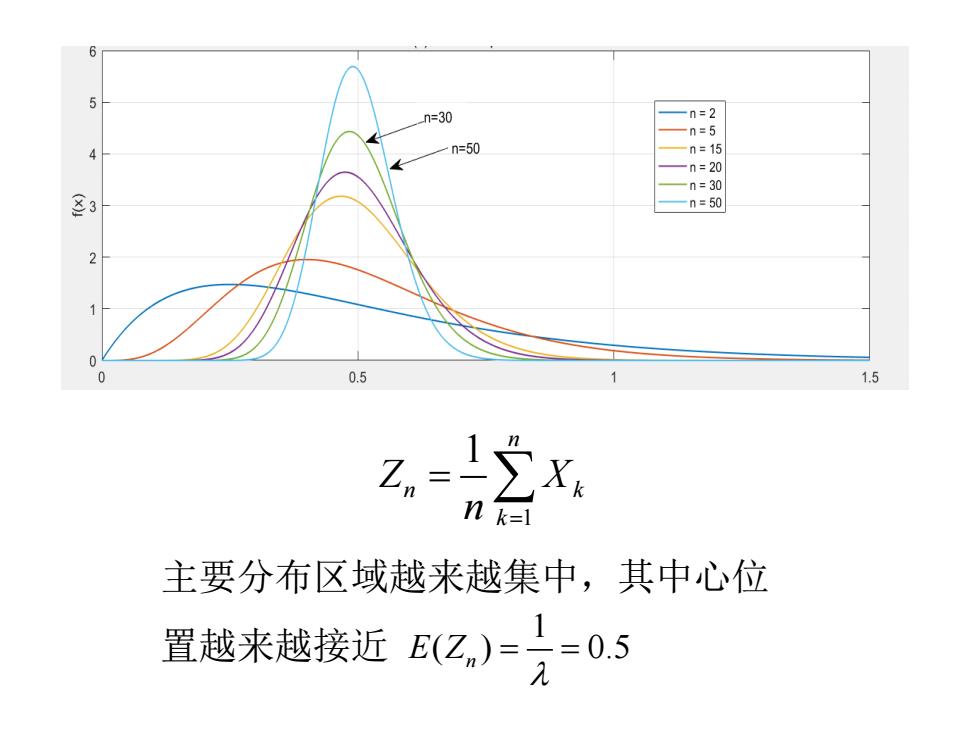
1 1 n n k k Z X n = = ∑ 主要分布区域越来越集中,其中心位 置越来越接近 1 ( ) 0.5 E Z n λ = =

定理1 独立同分布的中心极限定理 设随机变量序列X1,X2,…,Xn,…相互 独立,服从同一分布,且有期望和方差: E(X&)=4,D(Xk)=o2>0,k=1,2,… 则对于任意实数x, ∑X-nu lim P k= n->oc
定理1 独立同分布的中心极限定理 设随机变量序列 X1, X2 ,, X n , 相互 独立,服从同一分布,且有期望和方差: E(Xk ) = µ , D(Xk ) =σ2 > 0 , k =1,2, 则对于任意实数 x , ∫ ∑ −∞ − = →∞ = ≤ − x t n k k n x e dt n X n P 1 2 2 2 1 lim π σ µ

注:记 no 则Ym为∑X的标准化随机变量. k= limP(Yn≤x)=Φ(x) 即n足够大时,Y,的分布函数近似于标准正态 随机变量的分布函数 y,(0,1) 近似 三X.=no.+近似服从N0wLo)
注: 则 Y n 为∑= n k Xk 1 的标准化随机变量. limP(Y x) (x) n n ≤ =Φ →∞ 即 n 足够大时,Y n 的分布函数近似于标准正态 随机变量的分布函数 σ µ n X n Y n k k n − = ∑=1 记 Y ~ N(0,1) n 近似 ∑= n k Xk 1 = nσY n + nµ ( , ) 2 近似服从 N nµ nσ

定理2 德莫佛一 拉普拉斯中心极限定理 (DeMoivre-Laplace 设Yn~B(n,p),0<p<1,n=1,2,. 则对任一实数x,有 小 lim P 2dt 即对任意的a<b, Ym~N(np,np(1-p)(近似)
定理2 德莫佛 — 拉普拉斯中心极限定理 (DeMoivre-Laplace ) 设 Y n ~ B( n , p) , 0 < p < 1, n = 1,2,… 则对任一实数 x,有 ∫−∞ − →∞ = ≤ − − x t n n x e dt np p Y np P 2 2 2 1 (1 ) lim π 即对任意的 a < b, ∫ − →∞ = ≤ − − < b a t n n b e dt np p Y np P a 2 2 2 1 (1 ) lim π Y n ~ N (np , np(1-p)) (近似)