
§2.3 连续型随机变量及其概率分布 一、 连续型随机变量的概念 定义设X是一随机变量,若存在一个非负 可积函数f(x),使得 F(x)=["f(t)dt -0<X<+0 其中F(x)是它的分布函数 则称X是连续型随机变量,f(x)是它的 概率密度函数(p.d.f.),简称为密度函数 或概率密度 注1:连续性随机变量的分布函数连续 注2:f(x)不唯一
§2.3 连续型随机变量及其概率分布 定义 设 X 是一随机变量,若存在一个非负 可积函数 f ( x ), 使得 = ∫ − ∞ < < +∞ −∞ F x f t t x x ( ) ( )d 其中F ( x )是它的分布函数 则称 X 是连续型随机变量,f ( x )是它的 概率密度函数( p.d.f. ),简称为密度函数 或概率密度 一、连续型随机变量的概念 注1:连续性随机变量的分布函数连续. 注2:f (x) 不唯一
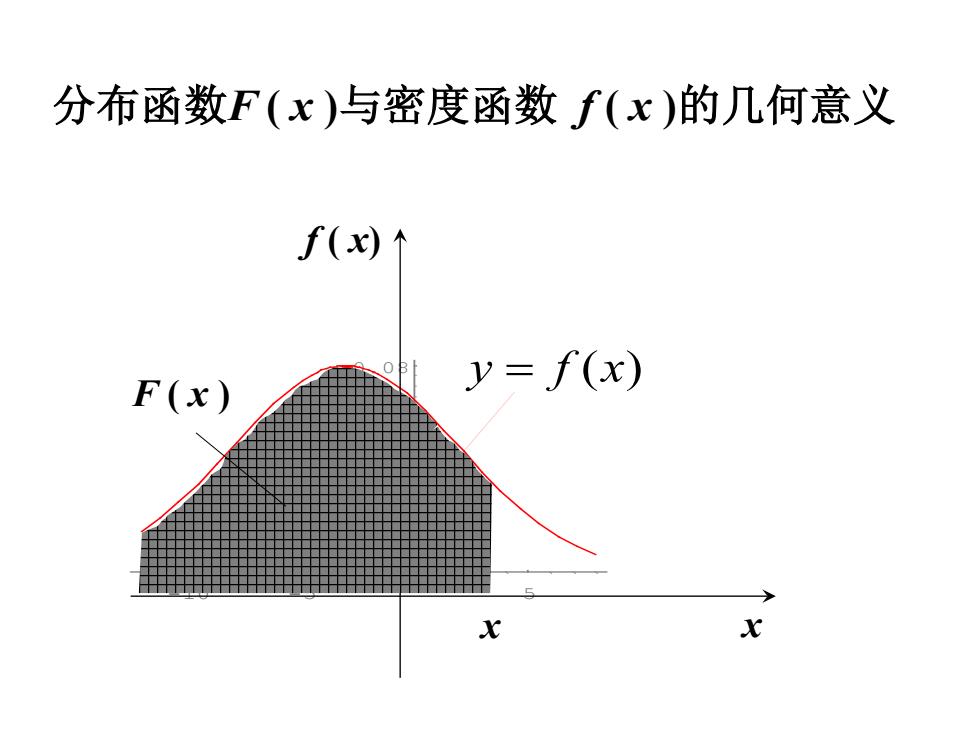
分布函数F(x)与密度函数f(x)的几何意义 f(x)个 F(x) y=f(x) X
-10 -5 5 0.02 0.04 0.06 0.08 x f ( x) x F ( x ) 分布函数F ( x )与密度函数 f ( x )的几何意义 y = f (x)

p.d.f.f(x)的性质 1、f(x)≥0 2、f(x)dx=F(+o)=1 常利用这两个性质检验一个函数能否作为连续性 随机变量的密度函数,或求其中的未知参数 3、在f(x)的连续点处,f(x)=F'(x) f(x)描述了X在x附近单位长度的区间内 取值的概率 f(x,)△x≈P(x,<X≤x,+△x)
p.d.f. f ( x )的性质 1、 f (x) ≥ 0 2、 ( )d = (+∞) =1 ∫ +∞ −∞ f x x F 常利用这两个性质检验一个函数能否作为连续性 随机变量的密度函数,或求其中的未知参数 3、 在 f ( x ) 的连续点处, f (x) = F′(x) f ( x ) 描述了X 在 x 附近单位长度的区间内 取值的概率 0 00 f x x Px X x x () ( ∆ ≈ < ≤ +∆ )

注意:对于连续型随机变量X,P(X=)=0 这里a可以是随机变量X的一个可能的 取值 事实上(X=a)c(a-x<X≤a) x>0 0≤P(X=a≤P(a-Ar<X≤a)=”f(x)dx 0≤P(X=a)≤1imf(x)dx=0 P(X=a)=0 命题 连续型随机变量取任一常数的概率为零 强调概率为0()的事件未必不发生(发生)
注意: 对于连续型随机变量X , P ( X = a) = 0 这里 a 可以是随机变量 X 的一个可能的 取值 0 ≤ P(X = a) ≤ P(a − ∆x < X ≤ a) ∫ − = a a x f x x ∆ ( )d →+ ∫ − ≤ = ≤ a x a x P X a f x x ∆ ∆ 0 ( ) lim ( )d 0 = 0 P(X = a) = 0 命题 连续型随机变量取任一常数的概率为零 事实上 (X = a) ⊂ (a − ∆x < X ≤ a) ∆x > 0 强调 概率为0 (1) 的事件未必不发生(发生)
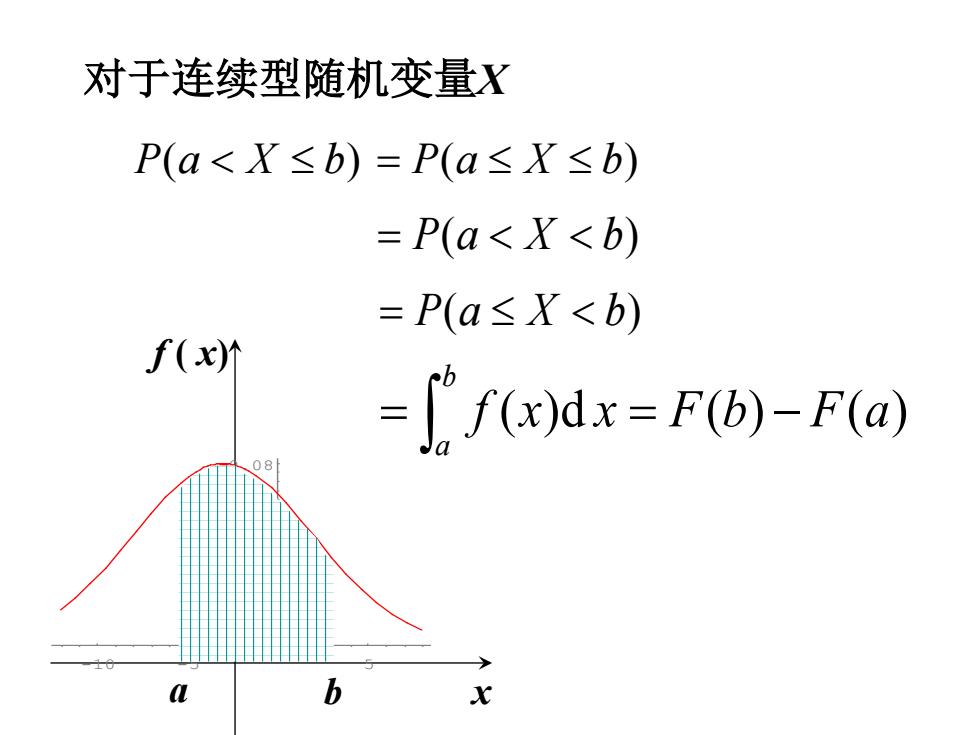
对于连续型随机变量X P(a<X≤b)=P(a≤X≤b) =P(a<X<b) =P(a≤X<b) f(x)外 =f(x)dx=F(b)-F(@) b
对于连续型随机变量X P(a < X ≤ b) = P(a ≤ X ≤ b) = P(a < X < b) = P(a ≤ X < b) f (x)d x F(b) F(a) b a = = − ∫ b x f ( x) -10 -5 5 0.02 0.04 0.06 0.08 a