
4.2方差 引例检验两批灯泡的质量,从中分别随机抽样5只, 测得使用寿命(单位:小时)如下: A:20001500 1000 500 1000 B:15001500 10001000 1000 试比较这两批灯泡质量的好坏 计算得:平均寿命分别为:A:1200B:1200 数学期望 方差 观察得:A中使用寿命偏离较大,B中使用寿命 偏离较小,所以,B产品质量较好
4.2 方差 引例 检验两批灯泡的质量,从中分别随机抽样5只, 测得使用寿命(单位:小时)如下: A: 2000 1500 1000 500 1000 B: 1500 1500 1000 1000 1000 试比较这两批灯泡质量的好坏 计算得:平均寿命分别为:A:1200 B:1200 观察得:A中使用寿命偏离较大,B中使用寿命 偏离较小,所以,B产品质量较好 数学期望 方差

1.方差的定义 定义:设X是一个随机变量,若E(X-EX)2存在 则称E(X-EX)2为X的方差,记为DX,即 方差 DX=E(X-EX) 均方差(标准差)ox=VDX (X-EX)2— 随机变量X的取值偏离平均值的 情况,是X的函数,也是随机变量 EX-EX)2一随机变量X的取值偏离平均值 的平均偏离程度—数 注:方差反映了随机变量相对其均值的偏离程度
2 2 ,( ) , () , , X E X EX E X EX X DX − − 设 是一个随机变量 若 存在 则称 为 的方差 记为 即 1. 方差的定义 (X - EX)2 —— 随机变量X 的取值偏离平均值的 情况, 是X的函数, 也是随机变量 E(X - EX)2 —— 随机变量X的取值偏离平均值 的平均偏离程度—— 数 定义: 2 方差 DX E X EX = − ( ) ( ) 均方差 标准差 σ X = DX 注: 方差反映了随机变量相对其均值的偏离程度

若X为离散型随机变量,概率分布为 P(X=Xk)=pk,k=1,2,… DX=∑(x&-EX}P 若X为连续型随机变量,概率密度为f(x) DX=∫(x-EX}f(x)d 常用的计算方差的公式: DX=EX2-(EX)
P(X = xk ) = pk , k = 1,2, 若 X 为离散型随机变量,概率分布为 = ∑( − ) k k k DX x EX p 2 若 X 为连续型随机变量,概率密度为f (x) DX (x EX) f (x)dx 2 ∫ +∞ −∞ = − 常用的计算方差的公式: 2 2 DX EX EX = − ( )
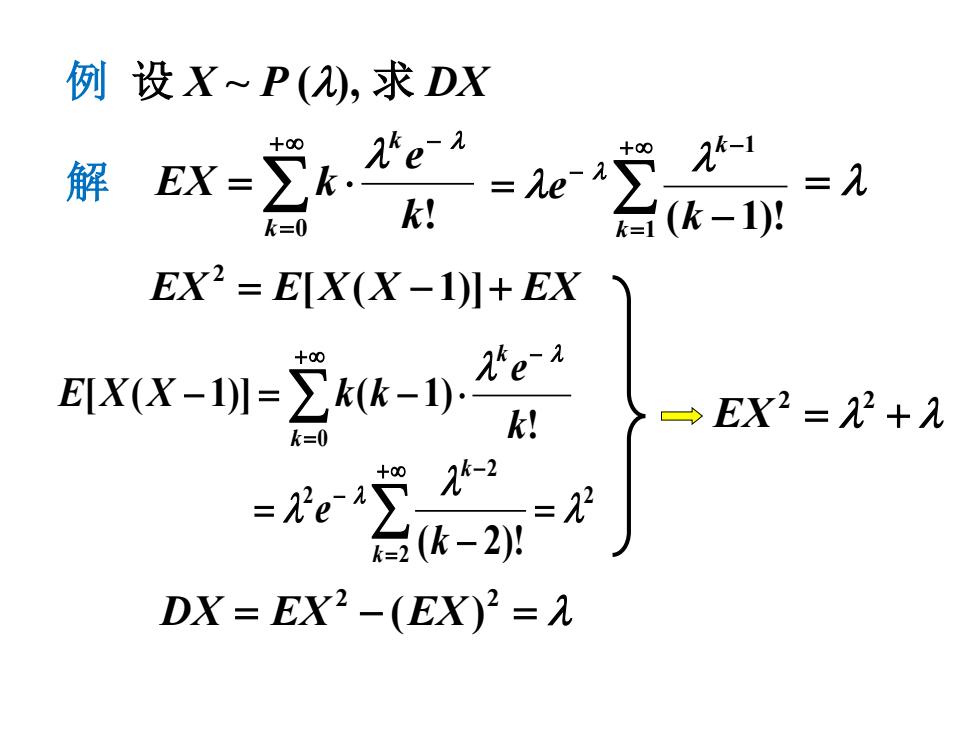
例设X~P(2),求DX +0 解 EX= . 2-1 =见 k=0 k! 台(k-1)月 EX2=EX(X-1)川+EX XX-叨=kk-). 十00 →EX2=22+孔 k=0 +0 =e 1-2 =12 k-2 DX=EX2-(EX)2=入
例 设 X ~ P (λ), 求 DX 解 ∑ +∞ = − = ⋅ 0 ! k k k e EX k λ λ ∑ +∞ = − − − = 1 1 ( 1)! k k k e λ λ λ = λ EX = E[X(X − 1)]+ EX 2 ! [ ( 1)] ( 1) 0 k e E X X k k k k λ λ +∞ − = − = ∑ − ⋅ 2 2 2 2 ( 2)! λ λ λ λ = − = ∑ +∞ = − − k k k e = λ + λ 2 2 EX = − = λ 2 2 DX EX (EX)

例设X~U(a,b),求DX 解DX=EX2-(EX)2 ='-( (b-a)2 12
解 DX 2 2 = − EX EX ( ) 2 2 1 ( ) 2 b a a b x dx b a + = − − ∫ 2 ( ) 12 b a − = 例 设 X ~ U( a , b),求 DX