上海交通大学：《概率论与数理统计》课程教学资源（课件讲义）第二章 随机变量及其分布 2.2 离散型随机变量及其概率分布

2.2 离散型随机变量及其概率分布 离散随机变量及分布律 定义若随机变量X的可能取值是有限多个 或无穷可列多个，则称X为离散型随机变量 描述离散型随机变量的概率特性常用它的概 率分布或分布律，即 P(X=xx)=pk,k=1,2,… 或 X X1 X2 XK P2 Pk

2.2 离散型随机变量及其概率分布 离散随机变量及分布律 定义 若随机变量 X 的可能取值是有限多个 或无穷可列多个，则称 X 为离散型随机变量 描述离散型随机变量的概率特性常用它的概 率分布或分布律，即 P(X = xk ) = pk , k =1,2,  X x1 x2 … xK … P p1 p2 … pk … 或

或 X~ X 水… 概率分布的性质 P%≥0，k=1,2,… 非负性 ∑P=1 规范性 k=

X ~ 或 1 2 k xx x   1 2 k pp p   概率分布的性质  pk ≥ 0, k =1,2, 非负性  1 1 ∑ = ∞ k= k p 规范性

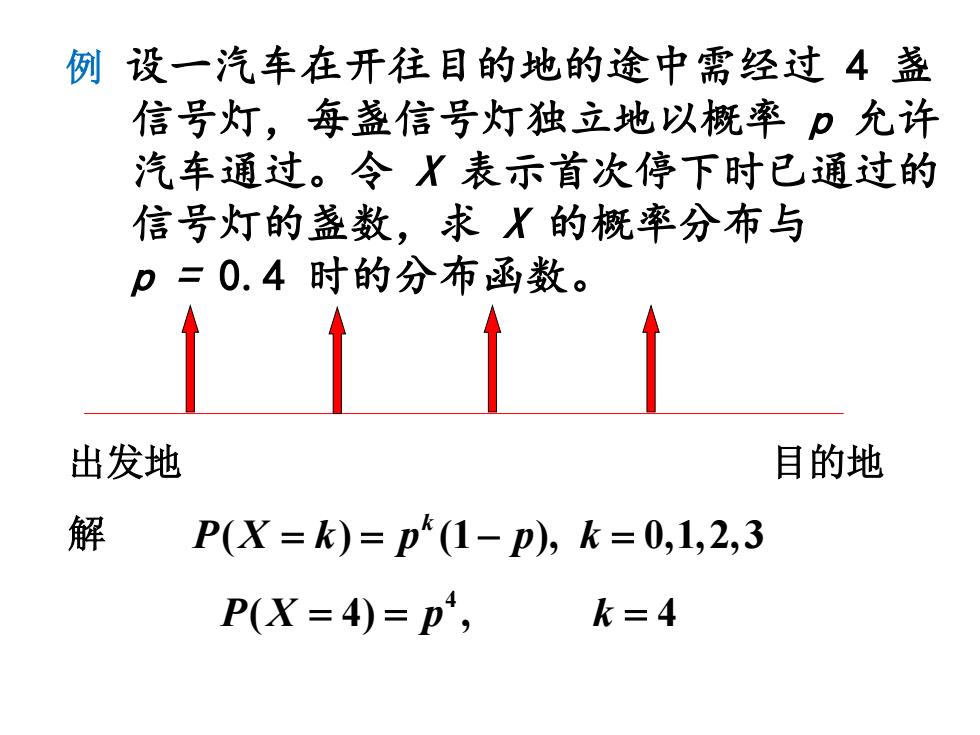
例设一汽车在开往目的地的途中需经过4盏 信号灯，每盏信号灯独立地以概率p允许 汽车通过。令X表示首次停下时已通过的 信号灯的盏数，求X的概率分布与 p=0.4时的分布函数。 出发地 目的地 解 P(X=k)=p(1-p),k=0,1,2,3 P(X=4)=p4, k=4

例 设一汽车在开往目的地的途中需经过 4 盏 信号灯，每盏信号灯独立地以概率 p 允许 汽车通过。令 X 表示首次停下时已通过的 信号灯的盏数，求 X 的概率分布与 p = 0.4 时的分布函数。 出发地 目的地 ( ) (1 ), 0,1,2,3 k 解 PX k p p k == − = 4 PX p k ( 4) , 4 = = =

当 p=0.4 k 0 1 2 3 4 0.60.4×0.60.42×0.60.43×0.6 0.44

当 p = 0.4 0.6 0.4´0.6 0.42´0.6 0.43´0.6 0.44 k pk 0 1 2 3 4

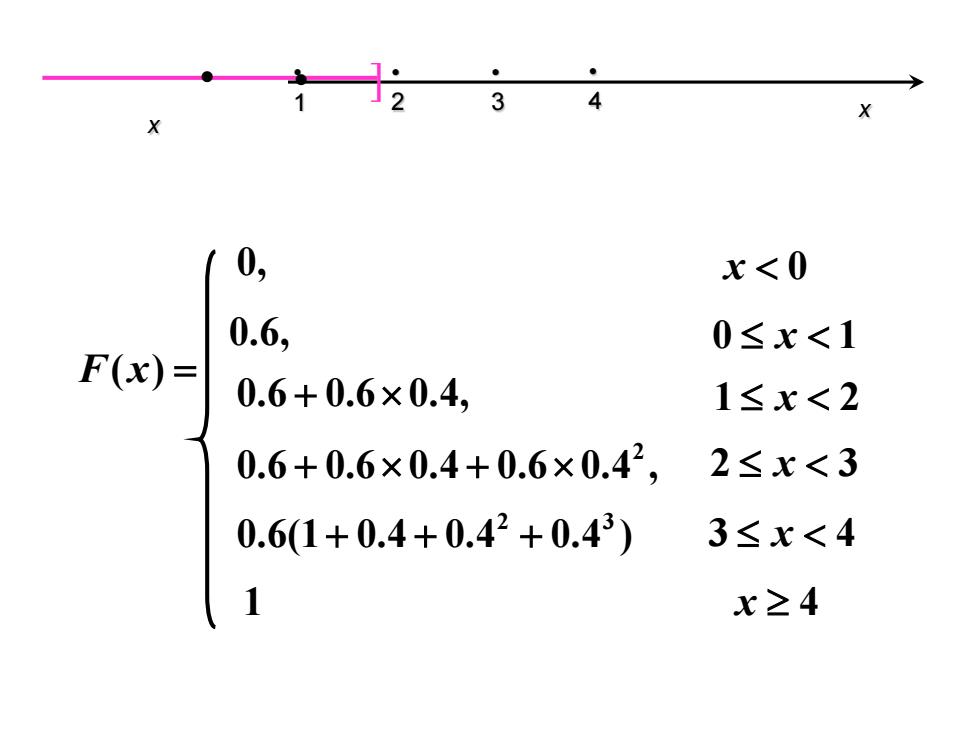
1 3 4 0, x<0 0.6, 0≤x<1 F(x)= 0.6+0.6×0.4, 1≤x<2 0.6+0.6×0.4+0.6×0.42， 2≤x<3 0.6(1+0.4+0.42+0.43) 3≤x<4 1 x≥4

• 0 • 1 • 2 • 3 • 4 x x ] ] 0.6 0.6 0.4, + × 1 2 ≤ < x 0.6, 0 1 ≤ < x 0, x < 0 2 0.6 0.6 0.4 0.6 0.4 , +×+× 2 3 ≤ < x 2 3 0.6(1 0.4 0.4 0.4 ) ++ + 3 4 ≤ < x 1 x ≥ 4 F x( ) = ]• • • ]