
8.2单个正态总体的参数检验 1、关于4的检验 拒绝域的推导 给定显著性水平与样本值(X1,2,,Xn) 设X~W(4,o),σ已知,需检验: H:u=40:H1:u+40 构造统计量 U=X-1o-N(0.) n
8.2 单个正态总体的参数检验 拒绝域的推导 设 X ~N ( µ, σ2),σ2 已知,需检验: H0 : µ = µ0 ; H1 : µ ≠µ0 构造统计量 ~ (0,1) 0 N n X U σ − µ = 给定显著性水平α与样本值(x1,x2,…,xn ) 1、关于µ 的检验

P(拒绝H|H为真) =P(X-4购≥k4=4)=Pa(X-4购≥k) =P( X-Ho )=PH X-Ho ≥Z)= 取k三Zg 所以本检验的拒绝域为 U≥ U检验法
P(拒绝H0|H0为真) ( ) = − µ0 ≥ µ = µ0 P X k ( ) 0 0 P X k = H − µ ≥ ( ) 0 0 n k n X PH σ σ µ ≥ − = α σ µ ≥ α = − = ( ) 2 0 0 Z n X PH n k Z σ α 2 取 = 所以本检验的拒绝域为 0: 2 U ≥ zα U 检验法
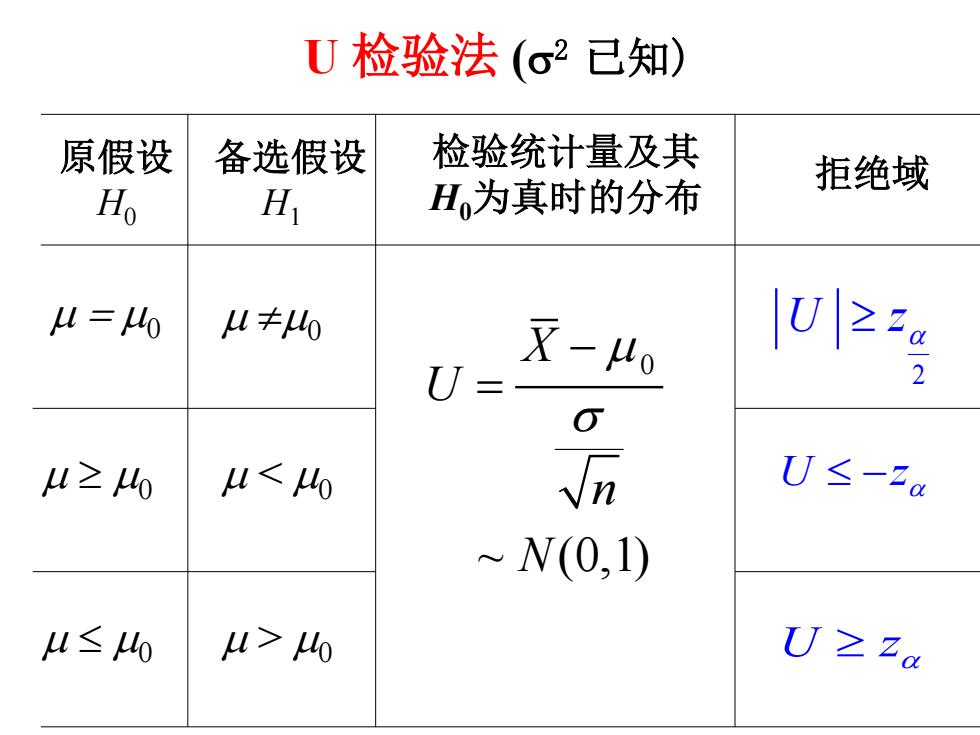
U检验法(o2已知) 原假设 备选假设 检验统计量及其 拒绝域 Ho H H为真时的分布 4=0 4丰0 U= X-Ho 10iz% u≥40 4<40 U≤-za ~N(0,1) W≤0 4>40 U≥za
µ = µ0 µ ≠µ0 µ ≥ µ0 µ ≤ µ0 µ < µ0 µ > µ0 2 U z ≥ α U z ≤ − α U z ≥ α U 检验法 (σ2 已知) 原假设 H0 备选假设 H1 检验统计量及其 H0为真时的分布 拒绝域 0 ~ (0,1) X U n N µ σ − =
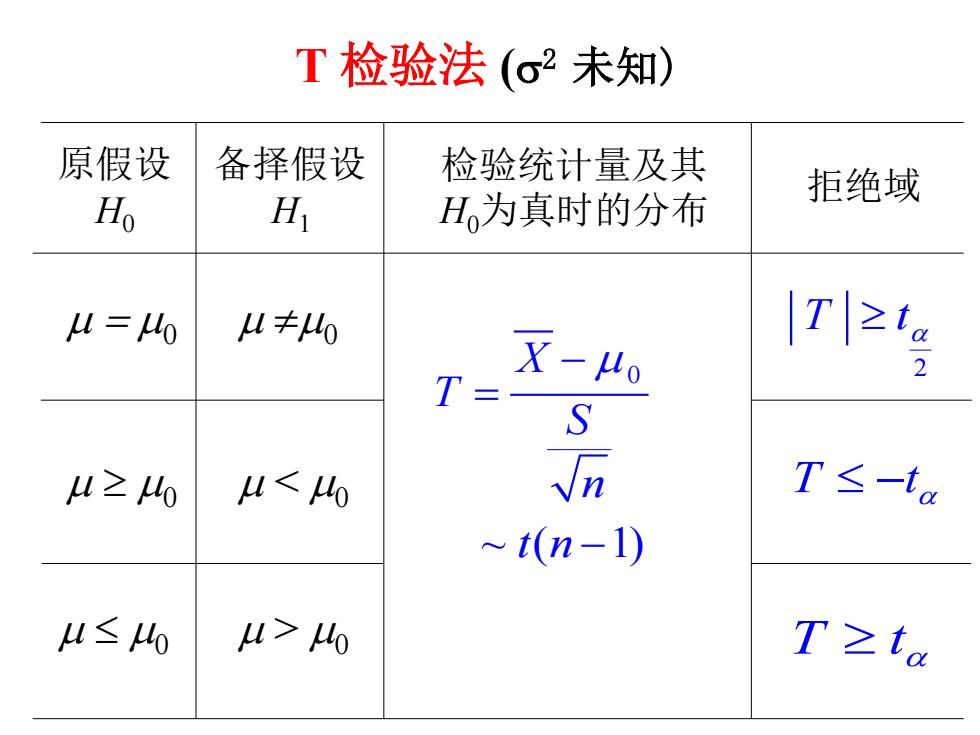
T检验法(σ2未知) 原假设 备择假设 检验统计量及其 Ho H H为真时的分布 拒绝域 W=0 4≠0 |Tl≥1a T= X-Ho S W≥40 L<40 n T≤-ta t(n-1 u≤0 u>40 T≥ta
µ = µ0 µ ≠µ0 µ ≥ µ0 µ ≤ µ0 2 T t ≥ α µ < µ0 µ > µ0 T t ≥ α T t ≤ − α 0 ~ ( 1) X T S n t n − µ = − T 检验法 (σ2 未知) 原假设 H0 备择假设 H1 检验统计量及其 H0为真时的分布 拒绝域

例某厂生产小型马达,其说明书上写着: 这种小型马达在正常负载下平均消耗电流不 会超过0.8安培. 现随机抽取16台马达试验,求得平均消 耗电流为0.92安培,消耗电流的标准差为 0.32安培. 假设马达所消耗的电流服从正态分布, 取显著性水平为=0.05,问根据这个样 本,能否否定厂方的断言?
例 某厂生产小型马达, 其说明书上写着: 这种小型马达在正常负载下平均消耗电流不 会超过0.8 安培. 现随机抽取16台马达试验, 求得平均消 耗电流为0.92安培, 消耗电流的标准差为 0.32安培. 假设马达所消耗的电流服从正态分布, 取显著性水平为α = 0.05, 问根据这个样 本, 能否否定厂方的断言?