
4、解题步骤1)根据问题的具体情况,选取一个变量例如x为积分变量,并确定它的变化区间[a,b];2)设想把区间[a,bl分成n个小区间,取其中任一小区间并记为[x,x+dx],求出相应于这小区间的部分量△AU的近似值.如果AU能近似地表示为[a,bl上的一个连续函数在x处的值f(x)与dx的乘积,就把f(x)dx称为量U的元素且记作dU, 即dU = f(x)dx;3)以所求量U的元素f(x)dx为被积表达式,在区间[a,b]上作定积分,得U=f(x)dx即为所求量U
1)根据问题的具体情况,选取一个变量例如x 为 积分变量,并确定它的变化区间[a,b]; 2)设想把区间[a,b]分成 n 个小区间,取其中任 一小区间并记为[x, x + dx],求出相应于这小区 间的部分量U的近似值.如果U 能近似地表 示为[a,b]上的一个连续函数在x处的值 f (x)与 dx的乘积,就把 f (x)dx称为量U 的元素且记 作dU,即 dU = f (x)dx ; 3)以所求量U 的元素 f (x)dx为被积表达式,在 区间[a,b]上作定积分,得 = b a U f (x)dx, 即为所求量U . 4、解题步骤 6
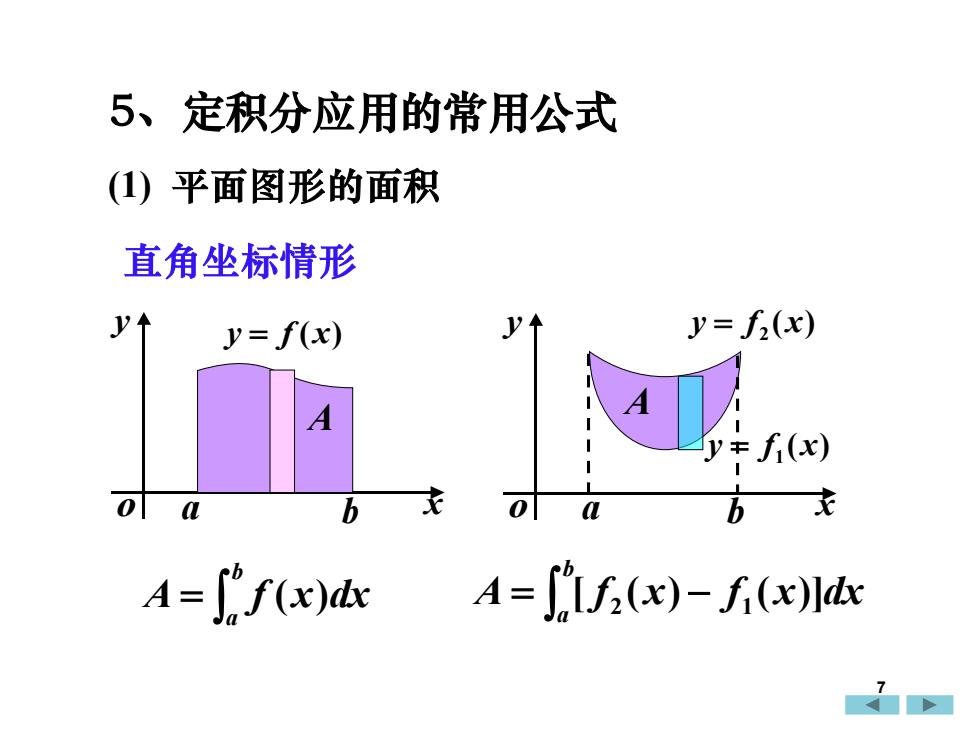
5、定积分应用的常用公式(1)平面图形的面积直角坐标情形y= f,(x)y1y= f(x)Afi(x)V丰1-txo1obbaa["f(x)dx(If2(x) - f(x)]dx
5、定积分应用的常用公式 (1) 平面图形的面积 x y o y = f (x) = b a A f (x)dx x y o ( ) y = f 1 x ( ) y = f 2 x = − b a A [ f2 (x) f1 (x)]dx A A 直角坐标情形 a b a b 7

参数方程所表示的函数x = p(t)如果曲边梯形的曲边为参数方程y=y(t)曲边梯形的面积 A=y(t)p'(t)dt(其中t,和t,对应曲线起点与终点的参数值)在[t,t,](或[t2,t])上x=β(t)具有连续导数y=y(t)连续
如果曲边梯形的曲边为参数方程 = = ( ) ( ) y t x t 曲边梯形的面积 = 2 1 ( ) ( ) t t A t t dt (其中 1 t 和 2 t 对应曲线起点与终点的参数值) 在[ 1 t , 2 t ]( 或[ 2 t , 1 t ]) 上x = (t)具有连续导数, y =(t)连续. 参数方程所表示的函数 8
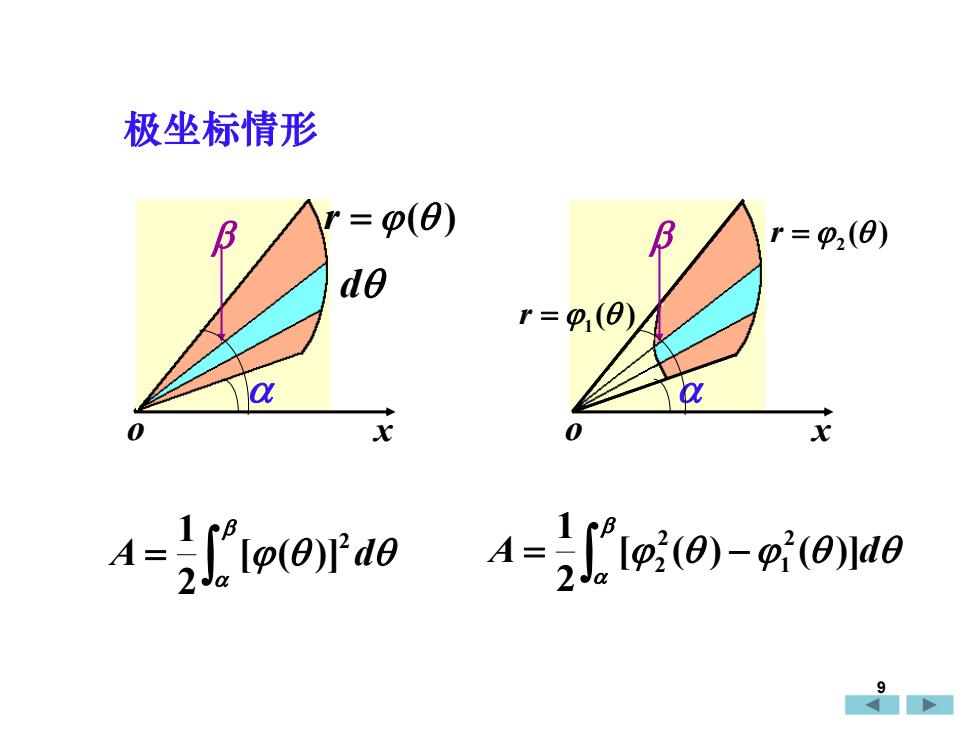
极坐标情形= β(0)Br = Φ2(0)3der = Φ(0)αa0x0x" [2(0) -(0)]d0[p()]'d12Ja9
= A d 2 [ ( )] 2 1 o x d r = ( ) o x ( ) r = 2 ( ) r = 1 = − A [ ( ) ( )]d 2 1 2 1 2 2 极坐标情形 9

(2) 体积yt (. 元[f(x)] dx0xxdxbaV[p(y)]’ dyx =p(y)0x10
(2) 体积 x x + dx x y o V f x dx b a 2 [ ( )] = V y dy d c 2 [( )] = x y o x = ( y) c d 10