一、空间直角坐标系第五章向量与空间解析几何三条坐标轴中的两条可确定一个平面称为坐标面:xOyyOz,zOx平面,它们把空间分成了八个卦限,在xOv面上逆时针依次为I、Ⅱ、I、IV卦限,下面依次为V、VI、VII、VI表示,如图5-4所示ⅡI1元VI图5-4
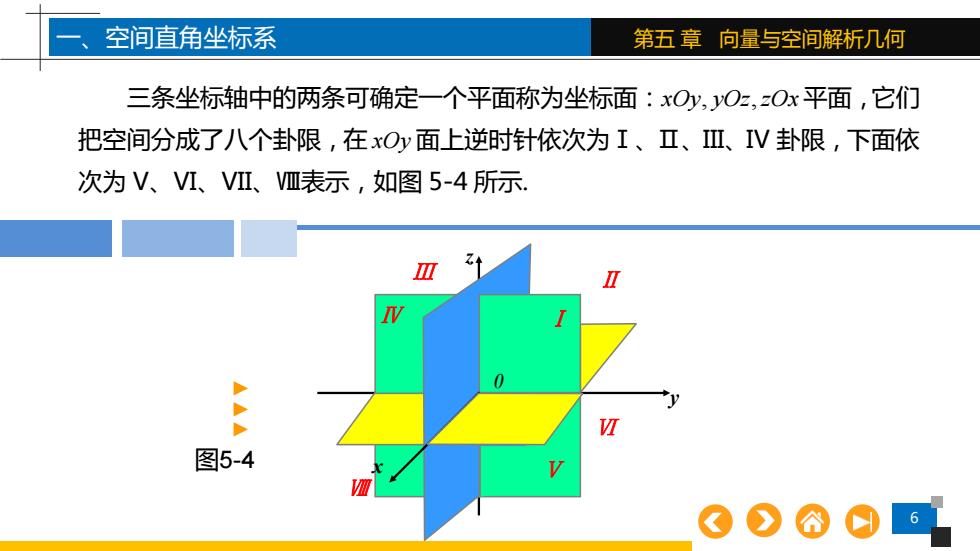
6 第五 章 向量与空间解析几何 三条坐标轴中的两条可确定一个平面称为坐标面:xOy yOz zOx , , 平面,它们 把空间分成了八个卦限,在 xOy 面上逆时针依次为Ⅰ、Ⅱ、III、IV 卦限,下面依 次为 V、VI、VII、Ⅷ表示,如图 5-4 所示. 一、空间直角坐标系 图5-4▲▲▲ z y x Ⅲ Ⅱ Ⅳ Ⅰ Ⅴ Ⅵ Ⅷ 0
一、空间直角坐标系第五章向量与空间解析几何对于空间一点M,过点M作三个平面分别垂直于x轴、y轴和z轴,它们与x轴、轴和z轴的交点依次为P、Q和R(见图5-5这三点在x轴、J轴和z轴上的坐标为x、y和z则这组有序数x、y和z称为点M的坐标记为 M(x,y,z).RM19图5-5
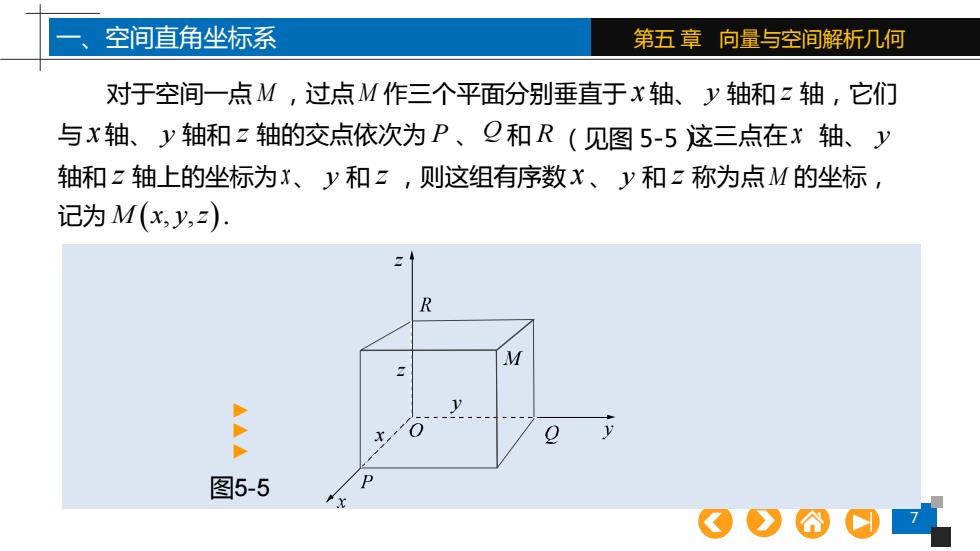
7 第五 章 向量与空间解析几何 对于空间一点M ,过点M 作三个平面分别垂直于 x 轴、 y 轴和 z 轴,它们 与 x 轴、 y 轴和 z 轴的交点依次为 P 、Q 和 R (见图 5-5), 图5-5 一、空间直角坐标系 z z x ▲▲▲ y 这三点在 x 轴 、 y 轴和 z 轴上的坐标为x、 y 和 z ,则这组有序数 x 、 y 和 z 称为点M 的坐标, 记为 M x y z ( , , )
一、空间直角坐标系第五章向量与空间解析几何反之,已知一有序数组x、y和z,我们可以在x轴、y轴和z轴上分别取坐标为x的点P,坐标为V的点O,坐标为Z的点R,过三个点分别作垂直于x轴、y轴和z轴的三个平面,它们相交于一点M,这M即为以x、y和z为坐标的点,所以通过直角坐标系,我们建立了空间点M与有序数组X、V和Z的一对应关系,见图5-6RLO8图5-6
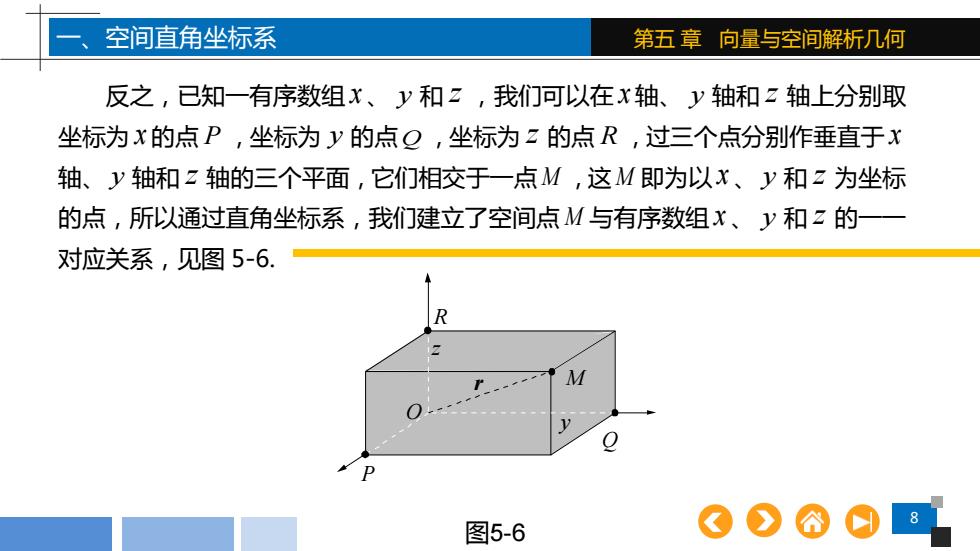
8 第五 章 向量与空间解析几何 反之,已知一有序数组 x 、 y 和 z ,我们可以在 x 轴、 y 轴和 z 轴上分别取 坐标为 x 的点 P ,坐标为 y 的点Q ,坐标为 z 的点 R ,过三个点分别作垂直于 x 轴、 y 轴和 z 轴的三个平面,它们相交于一点M ,这M 即为以 x 、 y 和 z 为坐标 的点,所以通过直角坐标系,我们建立了空间点 M 与有序数组 x 、 y 和 z 的一一 对应关系,见图 5-6. 图5-6 一、空间直角坐标系 z y x R P Q M O r

一、空间直角坐标系第五章向量与空间解析几何我们先来看几个特殊点的坐标:在xOy平面上:z=0,故对应点的坐标为A(x,y,0);在yOz平面上:x=0,故对应点的坐标为B(0,y,z);在zOx平面上:y=0,故对应点的坐标为C(x,0,2).在x轴上:y=z=0,点的坐标为P(x,0,0);B(0,,2)R(0.0,2)在y轴上:z=x=0,点的坐标为Q(0,y,0);MC(x,0,z)在z轴上:x=y=0,点的坐标为R(0,0,z)VQ(0,y,0)P(x,0,0)A(x,y,0)图5-609谷A
9 第五 章 向量与空间解析几何 我们先来看几个特殊点的坐标: 在 xOy 平面上: z = 0,故对应点的坐标为 A x y ( , ,0) ; 在 yOz 平面上: x = 0,故对应点的坐标为 B y z (0, , ); 在 zOx平面上: y = 0,故对应点的坐标为C x z ( ,0, ). 在 x轴上: y z = = 0,点的坐标为 P x( ,0,0) ; 在 y 轴上: z x = = 0 ,点的坐标为Q y (0, ,0) ; 在 z 轴上: x y = = 0,点的坐标为 R z (0,0, ). 图5-6 一、空间直角坐标系 z y x R(0,0,z) C(x,0,z) P(x,0,0) A(x,y,0) Q(0,y,0) B(0,y,z) M O r

一、空间直角坐标系第五章向量与空间解析几何设M(x,J,z)、M(x2,y2,=2)为空间两个点(见图5-7),通过M、M,各作三个分别垂直于三条坐标轴的平面,这六个平面组成一个以M,、M,为对角线的长方体,由此可得d=M,M=V(x2-x)+(y2-)+(z2-z)即d2=M,M=(2 -x)+(y2 -)+(z2 -z) ,M图5-710
10 第五 章 向量与空间解析几何 设 M x y z 1 1 1 1 ( , , )、 M x y z 2 2 2 2 ( , , )为空间两个点(见图 5-7),通过 M1 、M2 各作 三个分别垂直于三条坐标轴的平面,这六个平面组成一个以 M1 、M2 为对角线的长 方体, ( ) ( ) ( ) 2 2 2 2 2 1 2 2 1 2 1 2 1 即 d M M x x y y z z = = − + − + − , 由此可得 ( ) ( ) ( ) 2 2 2 1 2 2 1 2 1 2 1 d M M x x y y z z = = − + − + − . 图5-7 一、空间直角坐标系 ▲▲▲ z z2 y1 y2 y x M 1 M2 z1 x2 x1 O