
五、向量的模、方向角、投影 1、向量的模与两点间的距离公式: R 设产=(x,y,z),作OM=,则有 M T=OM =OP+00+OR 由勾股定理得 F=OM=OP+00+OR2=x2+y2+22 对两点4(x1,少,)与B(x2,y2,22),因 AB=OB-OA=(x2-x1,y2-1,22-1) 得两点间的距离公式: AB=AB=V(x2-x)2+(y2-y)2+(2-z)2
222 zyx r x y z),,,( 设 则有 OMr 2 2 2 OROQOP x o y z M N Q R P 由勾股定理得 ),,( 111 A x y z 因 得两点间的距离公式: ),,( 121212 x x y y z z 2 12 2 12 2 12 zzyyxx )()()( 对两点 与 ,),,( 222 B x y z rOM , 作 OMr OROQOP BABA AB OAOB 1、向量的模与两点间的距离公式: 五、向量的模、方向角、投影

练习已知点A5,3,1)和B(1,0,5),求与AB共线的单位向量e. 解因为AB=0B-0A=(1,0,5)-(5,3,1)=(-4,-3,4) 所以 |AB=V-42+(-3)2+42=V4T 于是 8=t 2=±(4,-3,4) 4BI V41
练习 已知点A(5,3,1)和B(1,0,5),求与 AB e . 共线的单位向量 解 因为 OAOBAB )1,3,5()5,0,1( ).4,3,4( .414)3()4(|| 2 22 所以 AB ).4,3,4( 41 1 || AB AB e 于是
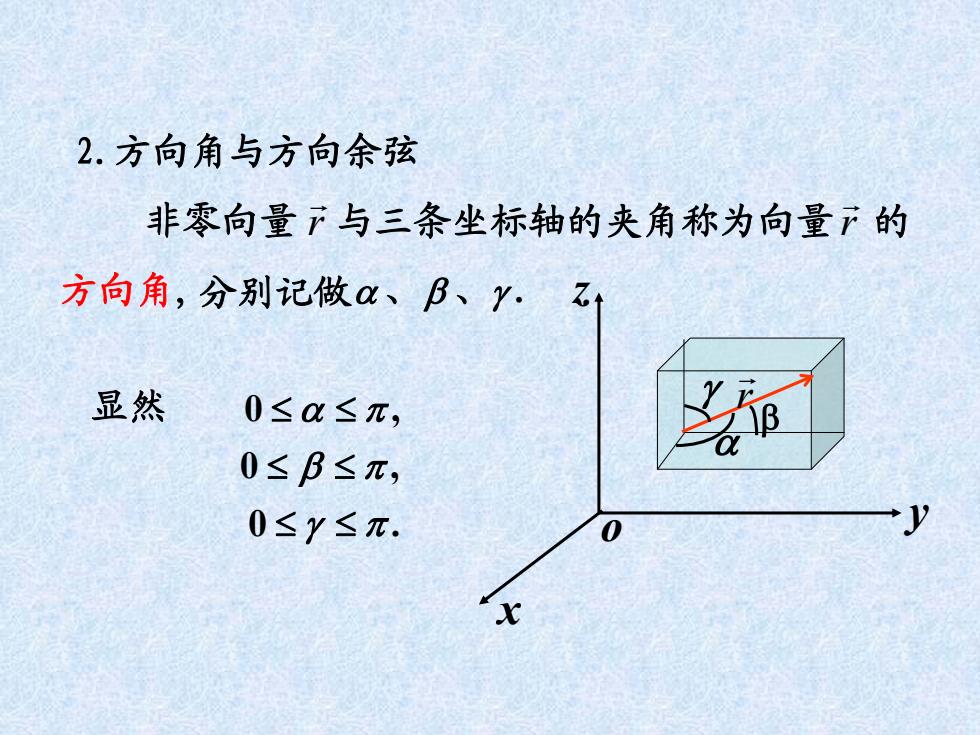
2.方向角与方向余弦 非零向量下与三条坐标轴的夹角称为向量广的 方向角,分别记做a、B、Y.乙t 显然 0≤a≤π, 0≤B≤π, 0≤y≤π
非零向量 与三条坐标轴的夹角称为向量 的 、 、 . ,0 ,0 .0 方向角, x y z o r 显然 2.方向角与方向余弦 分别记做 r r
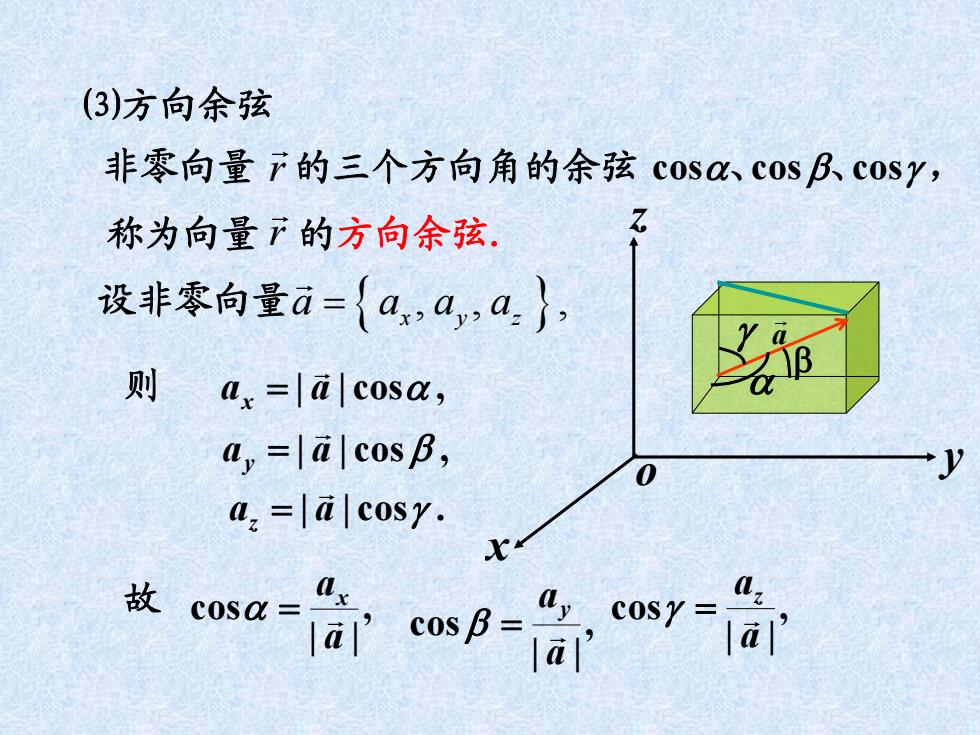
(3)方向余弦 非零向量r的三个方向角的余弦c0sa、c0sBc0sY, 称为向量下的方向余弦. 设非零向量a={a,a,a}, 则a.=|a|cosa, a,=lalcosB, 0 a.=lalcosy. 故 cosa= x s 1a ,o7=a y
非零向量 的三个方向角的余弦 coscoscos ,、、 a aaa xyz ,, , aa ,cos|| x aa ,cos|| y aa .cos|| z x y z o 称为向量 的方向余弦. ,|| cos a ax ,|| cos a ay ,|| cos aaz a ⑶方向余弦 则 故 r r 设非零向量
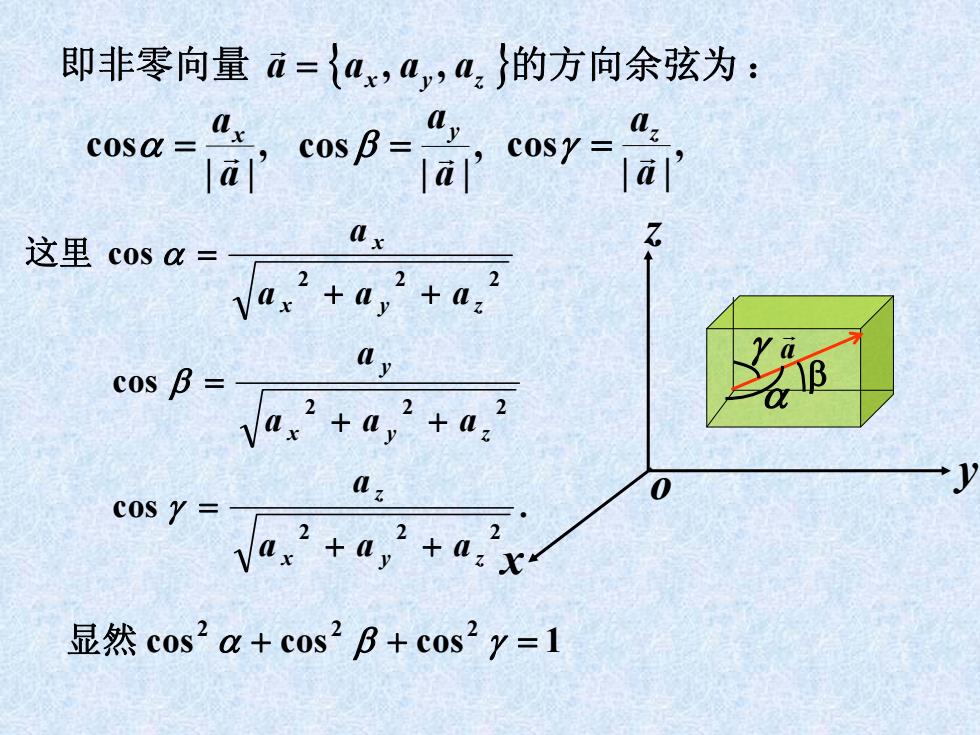
即非零向量a={a,,a}的方向余弦为: sa-备w8-w7=后 这里cosa= Va2+u,2+a2 ax cos B= V02+a,2+a2 cos y= ,ta.x 2 显然cos2a+cos2B+cos2y=1
即非零向量 ,, aaaa zyx 的方向余弦为 : cos cos 1cos 2 2 2 显然 cos . cos cos 222 222 222 zyx z zyx y zyx x aaa a aaa a aaa a 这里 ,|| cos a ax ,|| cos a ay ,|| cos aaz x y z o a