
定理1.设a为非零向量,则a∥b的充分必要条件是 存在唯一的实数入,使b=1d 题以是世)设x-以型 河-40哥-0 故b=d. (“唯一 设又有b=ua,则(2-m)a=0 性”) 而d≠0,故几-4=0,即九=4
定理1. 设a 为非零向量,则 证:(“必要性”) (“唯一 性”) 则 a∥b 设又有b=a , a 0)( a a b a a b 的充分必要条件是 存在唯一的实数,使 设 a∥b , b a 故 b a . b a . 而a 0, 故 0, 即 . ,取 则
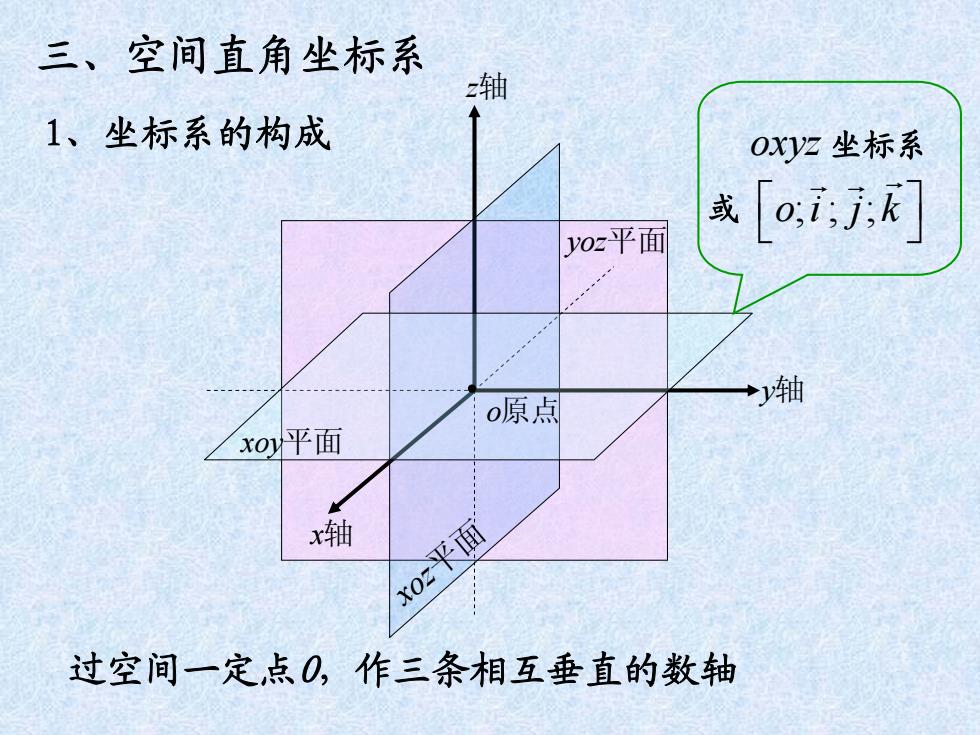
三、空间直角坐标系 z轴 1、坐标系的构成 Oxyz坐标系 或oi,j;k yoz平面 →轴 o原点 xoy平面 x轴 xoz平面 过空间一定点O,作三条相互垂直的数轴
x轴 y轴 z轴 o原点 xoy平面 xoz平面 yoz平面 过空间一定点O,作三条相互垂直的数轴 1、坐标系的构成 三、空间直角坐标系 oxyz 坐标系 或 o i;;;j k
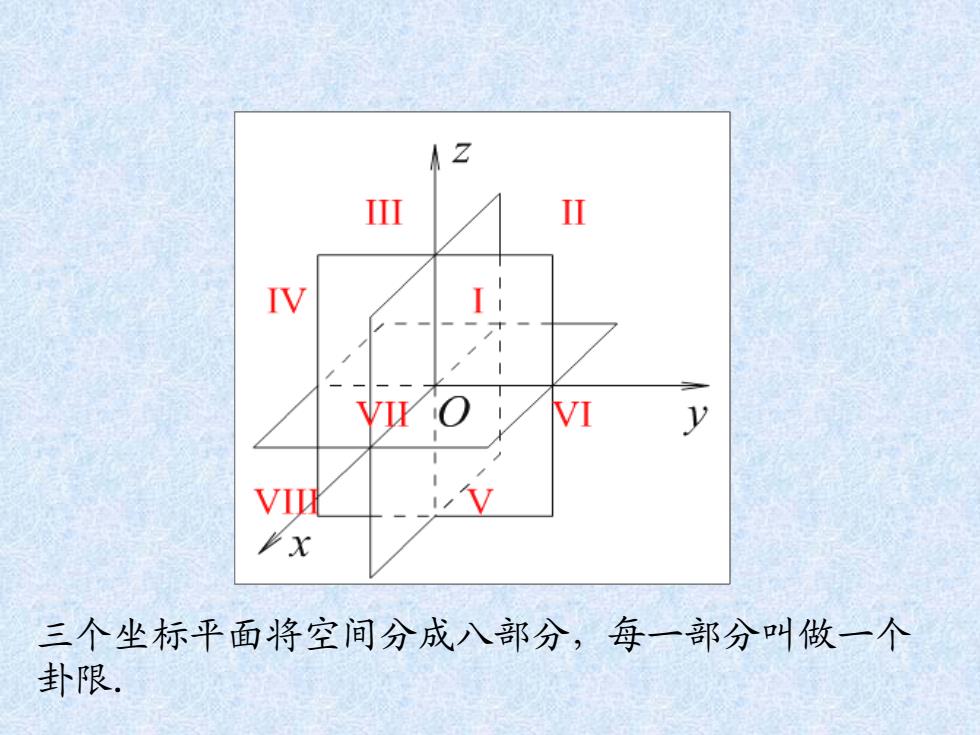
I VI VII 上x 三个坐标平面将空间分成八部分,每一部分叫做一个 卦限
三个坐标平面将空间分成八部分,每一部分叫做一个 卦限

2、向量的坐标表示 在空间直角坐标系下,任意向量下可用向径OM表示. 以i,,分别表示x,y,z轴上的单位向量,设,点M 的坐标为M(x,y,z),则 OM-ON+NM =04+0B+OC d OA=xi,OB=yj,OC=zk k r=xi+yj+zk=(x,y,2) A 此式称为向量下的坐标分解式, xi,yj,z称为向量开沿三个坐标轴方向的分向量
设点 M M x y z ,),,( 则 沿三个坐标轴方向的分向量. kzjyixr x y z),,( x o y z M N B C i j k A 以 ,, kji 分别表示 ,, zyx 轴上的单位向量 , 的坐标为 kzjyix r ,, 称为向量 r 任意向量 可用向径OM 表示. OM N NMO OCOBOA ixOA , jyOB , kzOC 2、向量的坐标表示 在空间直角坐标系下, r 此式称为向量 r 的坐标分解式,

四、利用坐标作向量的线性运算 1、向量的加减法与数乘 a=(ax,a,a,)=ai+ayj+ak; B=(bs,b,B:)=bi+byj+b.k; (1)加法d+b=(a.+b,a,+b,a2+b) =(a+b)i+(a,+b,)j+(a2+b)k; (2)减法d-b=(a-b,a,-b,a:-b) =(a.-b)i+(a,-b,)j+(a2-b)k (3)数乘a=(2ax,2a,a)=(a)i+(n,)j+(a,)k. 2、平行向量的坐标表示式 aWdb=a台(6,b,b)=a,4,0,) (等价→
),,( zyx aaaa ),,( bbbb zyx ⑴加法 ),,( zzyyxx babababa kbajbaiba ;)()()( xx yy zz 1、向量的加减法与数乘 kajaia ; zyx kbjbib ; zyx ),,( babababa zzyyxx kbajbaiba ;)()()( xx yy zz ⑵减法 ),,( aaaa zyx kajaia .)()()( x y z ⑶数乘 2、平行向量的坐标表示式 abba // ),,(),,( zyx aaabbb zyx z z y y x x a b a b a b 四、利用坐标作向量的线性运算 (等价)