
例设已知两,点M2,2,√2))和N(1,3,0),计算向量 MN的模、方向余弦和方向角. 解MN={1-2,3-2,0-V2}={-1,1,-√2y 1MNV-1)2+12+(-2)2=2; cosa coy
3 2 3 43 2 1 cos 2 1 cos 22 cos 解 例 MN }2,1,1{}20,23,21{ 设已知两点 (2,2, 2))和 (1, 3, 0), 计算向量 MN 的模、方向余弦和方向角. M | | ( 1) 1 ( 2) 2 2 2 2 MN N
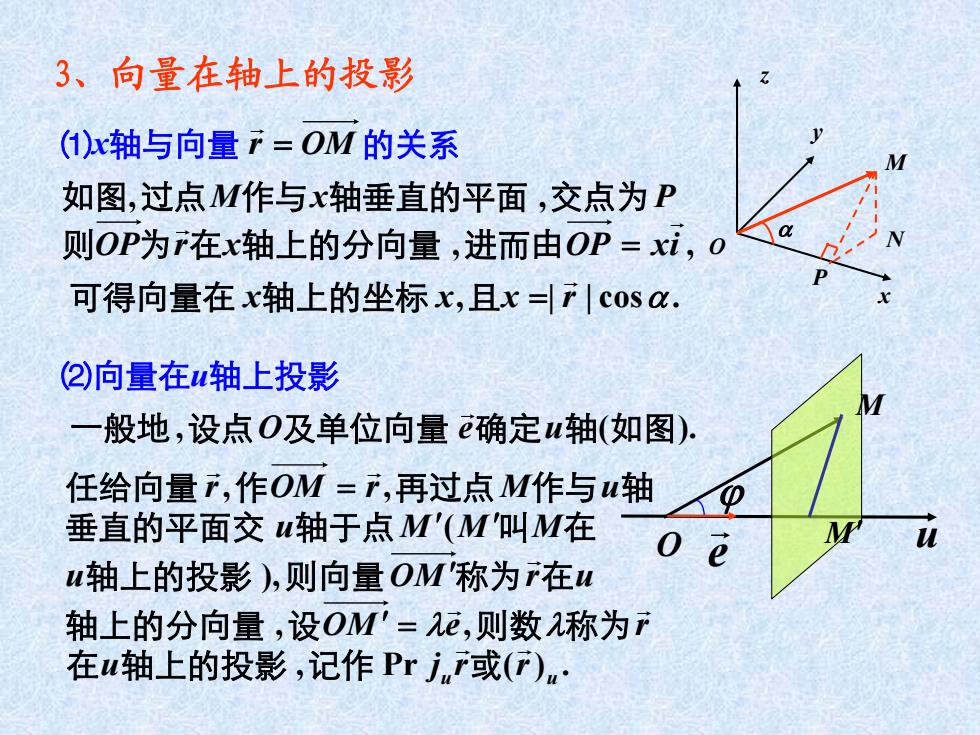
3、向量在轴上的投影 (1)x轴与向量产=OM的关系 如图,过点M作与x轴垂直的平面,交点为P 则OP为在x轴上的分向量,进而由OP=xi,o 可得向量在x轴上的坐标x,且x=产|cosa. ②)向量在轴上投影 一般地,设点O及单位向量确定u轴(如图). 任给向量产,作OM=f,再过点M作与u轴 垂直的平面交u轴于点M'(M'叫M在 M 轴上的投影),则向量OM'称为在W 轴上的分向量,设0M'=2,则数2称为7 在u轴上的投影,记作Prjr或(f)m
3、向量在轴上的投影 ,过点如图 作与xM 轴垂直的平面 ,交点为 P O z x y M N P ⑴x轴与向量 OMr 的关系 xrOP , ixOP , 在为则 轴上的分向量 进而由 x rxx .cos||, 可得向量在 轴上的坐标 且 ⑵向量在 u轴上投影 u M O M e 一般地 ,设点 O及单位向量 确定ue 轴 如图).( .)(Pr, , , ), ( , , u u u rrj eMO r u urMO MMMu uMrOMr 在 轴上的投影 记作 或 轴上的分向量 设 则数 称为 轴上的投影 则向量 称为 在 垂直的平面交 轴于点 在叫 任给向量 作 再过点 作与 轴

3)向量在三坐标轴上的投影 在直角坐标系Oxyz中的坐标ax,a,a,即i在三坐标轴上 的投影,即 as=Pr jxd,ay=Pr j,a,a:=Pr j.d 或记作a.-(a),a,=(d),a2=(a) ④)向量投影的性质 i)(a)=alcos(a,u) a+).=(@).+6) ii)(a)=(a)
的投影 即 在直角坐标系 中的坐标 即 在三坐标轴上 , a Oxyz ,, zyx aaaa ⑶向量在三坐标轴上的投影 ajaajaajax yx zy z Pr,Pr,Pr x x y y z aaaaaa z 或记作 ,, ⑷向量投影的性质 uaaai ),cos(||) u ) . u u babaii u ) . u aaiii u

例设m=3i+5j+8k,i=2i-4j-7k, p=5i+j-4k,求向量d=4m+3-p在x轴上 的投影及在y轴上的分向量. 解.∵d=4m+3n-p =4(3i+5j+8k)+3(2i-4j-7k) -(5i+j-4k) =13i+7j+15k, ∴.在x轴上的投影为ax=13, 在y轴上的分向量为7j:
例 设 kjim 853 , kjin 742 , kjip 45 ,求向量 pnma 34 在x轴上 的投影及在 y轴上的分向量. 解 pnma 34 kji )853(4 kji )742(3 kji )45( kji ,15713 在x轴上的投影为ax 13, 在 y轴上的分向量为 j 7

第二节数量积向量积 一、两向量的数量积 二、两向量的向量积
一、两向量的数量积 一、两向量的数量积 二、两向量的向量积 二、两向量的向量积 第二节 数量积 向量积