
定理2(极值第二判别法) 设函数f(x)在点xo处具有 二阶导数,且f'(x)=0,f"(x)≠0 (I)若f"(x)<0,则f(x)在点xo取极大值; (2)若f"(x)>0,则f(x)在点xo取极小值 证:(0)f"o)=1im)-f'l=1imf x→x0 x-X0 x→x0X-X0 由f”(x)<0知,存在6>0,当0<x-x<6时, f'(<0 x-Xo 故当x-6<x<xo时,f'(x)>0; 十 当x<x<x+6时,f'(x)<0, x08x0x+6 由第一判别法知f(x)在xo取极大值 (2)类似可证 oooo08
定理2 (极值第二判别法) 二阶导数 , 且 则 在点 取极大值 ; 则 在点 取极小值 . − + 证: (1) ( ) 0 f x 0 0 ( ) ( ) lim 0 x x f x f x x x − − = → 0 ( ) lim 0 x x f x x x − = → ( ) 0 , 由 f x0 知 存在 0, 0 , 当 x − x0 时 故当 x0 − x x0时,f (x) 0; 当x0 x x0 + 时,f (x) 0, 0 x 0 x0 − x + + − 由第一判别法知 ( ) . f x 在x0 取极大值 (2) 类似可证 . 机动 目录 上页 下页 返回 结束

例2.求函数f(x)=(x2-1)3+1的极值 解:1)求导数 f'(x)=6x(x2-1)2,f"(x)=6(x2-105x2-1) 2)求驻点 令f'(x)=0,得驻点x=-1,2=0,3=1 3)判别 因f"(0)=6>0,故f(0)=0为极小值; 又∫”(-1)="(1)=0,故需用第一判别法判别 由于f'(x)在x=±1左右邻域内不变号, .f(x)在x=±1没有极值」 OaoO⊙8
例2. 求函数 的极值 . 解: 1) 求导数 ( ) 6 ( 1) , 2 2 f x = x x − ( ) 6( 1)(5 1) 2 2 f x = x − x − 2) 求驻点 令 f (x) = 0, 得驻点 x1 = −1, x2 = 0, x3 =1 3) 判别 因 f (0) = 6 0, 故 为极小值 ; 又 f (−1) = f (1) = 0, 故需用第一判别法判别. 1 x y −1 机动 目录 上页 下页 返回 结束

定理3(判别法的推广)若函数f(x)在xo点有直到n阶导 数,且f'(0)="(x)=.=fn-少(xo)=0,fm(x)≠0, 则:1)当n为偶数时,x,为极值点,且 fm)()>0时,x是极小点; fm)(xo)<0时,x,是极大点 2)当n为奇数时,x,不是极值点 证:利用f(x)在x。点的泰勒公式,可得 fx)-f()=-+o(-") n! 当x充分接近x时,上式左端正负号由右端第一项确定, 故结论正确 eo0 n年h
定理3 (判别法的推广) ( ) 0, 0 ( ) f x n 则: 数 , 且 1) 当 n 为偶数时, 是极小点 ; 是极大点 . 2) 当 n 为奇数时, 为极值点 , 且 不是极值点 . f (x) = f (x0 ) + f (x0 )(x − x0 ) ++ n n x x n f x ( ) ! ( ) 0 0 ( ) − (( ) ) 0 n + o x − x − + 当 充分接近 时, 上式左端正负号由右端第一项确定 , 故结论正确 . 机动 目录 上页 下页 返回 结束 证: 利用 在 点的泰勒公式 , 可得
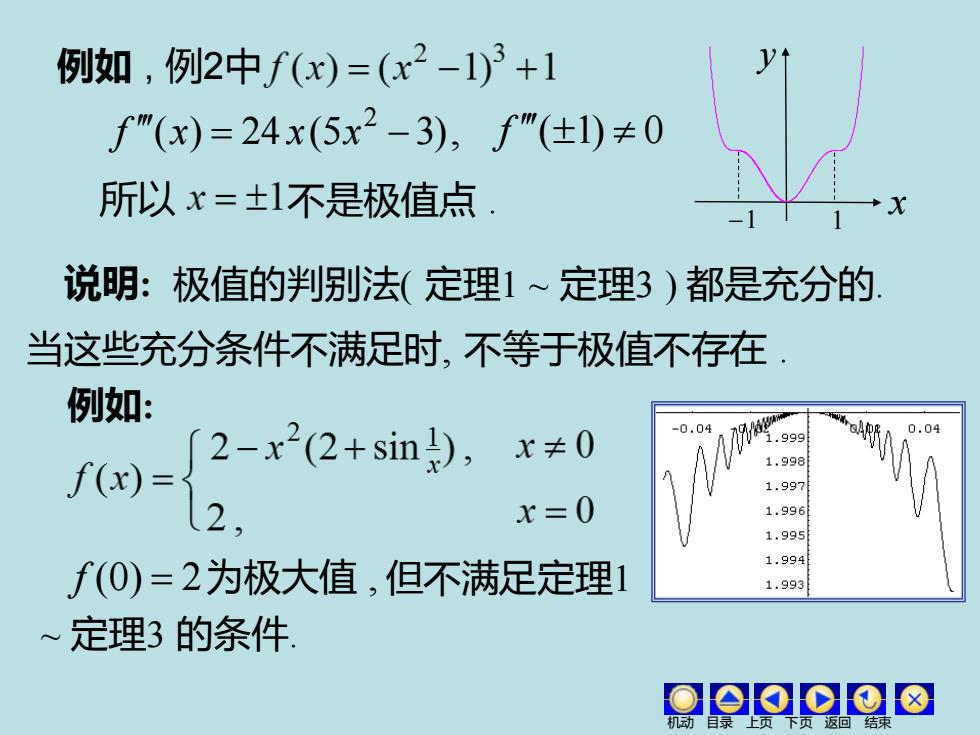
例如,例2中f(x)=(x2-1)3+1 f"(x)=24x(5x2-3),f"(±1)≠0 所以x=±1不是极值点: 说明:极值的判别法(定理1~定理3)都是充分的 当这些充分条件不满足时,不等于极值不存在 例如: f(x)= 「2-x2(2+sin),x≠0 .999 1.998 1.997 2 x=0 1.996 1.995 f(0)=2为极大值,但不满足定理1 1.994 1.993 ~定理3的条件
例如 , 例2中 ( ) 24 (5 3), 2 f x = x x − f (1) 0 所以 不是极值点 . 说明: 极值的判别法( 定理1 ~ 定理3 ) 都是充分的. 当这些充分条件不满足时, 不等于极值不存在 . 例如: f (0) = 2 为极大值 , 但不满足定理1 ~ 定理3 的条件. x y −1 1 机动 目录 上页 下页 返回 结束