
第一章 第十为 闭区间上连续西教的性质 一、最值定理 二、介值定理 *三、一致连续性 Oao⊙⊙☒
第十节 一、最值定理 二、介值定理 *三、一致连续性 机动 目录 上页 下页 返回 结束 闭区间上连续函数的性质 第一章

一、最值定理 定理1.在闭区间上连续的函数在该区间上一定有最大 值和最小值 即:设f(x)∈C[a,b],则351,52∈[a,b],使 f(s)=min f(x) a≤x≤b yy=f(x) f(s2)=max f(x) a≤x≤b (证明略) 0a5152bx 注意:若函数在开区间上连续,或在闭区间内有间断 点,结论不一定成立 OOo⊙O8
注意: 若函数在开区间上连续, 结论不一定成立 . 一、最值定理 定理1.在闭区间上连续的函数 即: 设 f (x)C[a, b], o x y a b y = f (x) 1 2 则 , [ , ], 1 2 a b 使 ( ) min ( ) 1 f f x a xb = ( ) max ( ) 2 f f x a xb = 值和最小值. 或在闭区间内有间断 在该区间上一定有最大 (证明略) 点 , 机动 目录 上页 下页 返回 结束
例如,y=x,x∈(0,1) 无最大值和最小值 又如, -x+1,0≤x<1 f)= 1,x=1 -x+3,1<x≤2 也无最大值和最小值 2
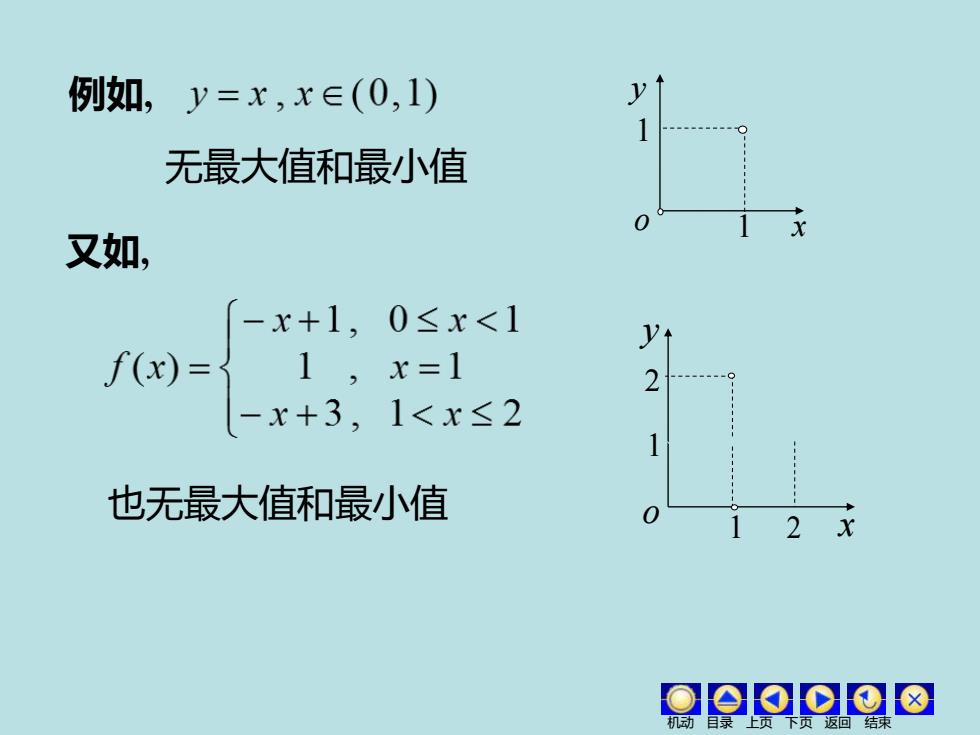
例如, 无最大值和最小值 o x y 1 1 x o y 1 1 2 2 也无最大值和最小值 又如, 机动 目录 上页 下页 返回 结束

推论.在闭区间上连续的函数在该区间上有界 证:设f(x)∈C[a,b],由定理1可知有 M=maf,m=mnf xEla,bl ) M y=f(x) 故x∈[a,b],有m≤f(x)≤M, 因此f(x)在[a,b]上有界 m 0a5152bx 二、介值定理 定理2.(零点定理)f)∈C[a,b],’y=) 且f(a)f(b)<0>至少有一点 5∈(a,b),使f(5)=0.(证明略)
o b x y a y = f (x) 1 2 m M 推论. 由定理 1 可知有 max ( ) , [ , ] M f x x a b = min ( ) [ , ] m f x x a b = 证: 设 上有界 . 二、介值定理 定理2. ( 零点定理 ) 且 至少有一点 使 x y o a b y = f (x) 机动 目录 上页 下页 返回 结束 ( 证明略 ) 在闭区间上连续的函数在该区间上有界

定理3.(介值定理)设f(x)∈C[a,b],且f(a)=A, f(b)=B,A≠B,则对A与B之间的任一数C,至少有 一点5∈(a,b),使f(5)=C. y=f(x) 证:作辅助函数 B (x)=f(x)-C A. 则p(x)∈C[a,b],且 b p(a)(b)=(A-C)(B-C)<0 故由零点定理知,至少有一点5∈(a,b),使p(5)=0, 即 f(5)=C. 推论:在闭区间上的连续函数必取得介于最小值与最 大值之间的任何值
定理3. ( 介值定理 ) 设 f (x)C[a, b], 且 f (a) = A, f (b) = B, A B , 则对 A 与 B 之间的任一数 C , 一点 证: 作辅助函数 (x) = f (x) −C 则 (x)C[a, b] , 且 (a) (b) = (A−C)(B −C) 故由零点定理知, 至少有一点 使 即 推论: A o b x y a y = f (x) B C 使 至少有 在闭区间上的连续函数必取得介于最小值与最 大值之间的任何值 . 机动 目录 上页 下页 返回 结束