
18 第1章有限单元法基本程式 求解方法可分为两类,即直接解法(例如高斯消去法、三角分解法、波前法等)和 迭代解法(例如超松弛迭代法、共轭梯度法等)。目前直接解法占主导地位,但在 大型问题中,更多采用的则是迭代解法。必须指出,代数方程组求解的效率在很 大程度上决定着有限元计算的效率,因此方程组解法备受重视。然而,本书不打 算介绍这方面的内容,因为它们是线性代数课程中介绍的基本部分。 求出节点位移后,计算单元应变、单元应力非常简单。事实上,只要按照前 述分析的步骤回代求解即可。 43y 【例题1.3】图1.8所示为一厚度为t的 弹性薄板,其材料的弹性模量为E,泊松比 v=0.2。单位长荷载g,不考虑重力。试计算 3) 弹性体的位移和应力。 解①结构离散化 将结构化分为三个单元,共5个节点,其 图ms州性薄梗 中节点3,4,5为固定边界点。 单元节点局部码与整体码的对应关系 单元号 2 局部码 2 2 2 整体码‖ 1 3 ②单元刚度矩阵 对于单元(1),可求得A=0.5,b1=0,b2=-1,b3=1,c1=1,c2=-1, c3=0。计算结果表明,三个单元的刚度矩阵相同,即 「0.4 0 -0.4-0.4 0 0.4 0 1 -0.2-10.2 0 k=×-0.410.6 -0.4-0.21.40.6 -1 -0.4 1.4 -0.2 -0.4 0 0.2 -1 -0.2 0 L0.4 0 -0.4-0.4 0 0.4 ③整体刚度方程 kPkS k是 k罗 k+ 0 k k2+k80 k+k2 k K- k出 0 k k2 0 k3+kk2+ k k+k+k k贸 0 k 0 k k
求解方法可分为两类,即直接解法(例如高斯消去法、三角分解法、波前法等)和 迭代解法(例如超松弛迭代法、共轭梯度法等)。目前直接解法占主导地位,但在 大型问题中,更多采用的则是迭代解法。必须指出,代数方程组求解的效率在很 大程度上决定着有限元计算的效率,因此方程组解法备受重视。然而,本书不打 算介绍这方面的内容,因为它们是线性代数课程中介绍的基本部分。 求出节点位移后,计算单元应变、单元应力非常简单。事实上,只要按照前 图18 弹性薄板 述分析的步骤回代求解即可。 【例题13】 图18所示为一厚度为t的 弹性薄 板,其 材 料 的 弹 性 模 量 为 E,泊 松 比 ν=02。单位长荷载q,不考虑重力。试计算 弹性体的位移和应力。 解 ①结构离散化 将结构化分为三个单元,共5个节点,其 中节点3,4,5为固定边界点。 单元节点局部码与整体码的对应关系 单元号 1 2 3 局部码 1231231 2 3 整体码 1342454 2 1 ②单元刚度矩阵 对于单元(1),可求得 A=05,b1=0,b2=-1,b3=1,c1=1,c2=-1, c3=0。计算结果表明,三个单元的刚度矩阵相同,即 Ke= Et 192× 04 0 -04 -04 0 04 0 1 -02 -1 02 0 -04 -02 14 06 -1 -04 -04 -1 06 14 -02 -04 0 02 -1 -02 1 0 熿 燀 燄 04 0 -04 -04 0 04燅 ③整体刚度方程 K= k(1) 11+k(3) 33 k(3) 32 k(1) 12 k(1) 13 +k(3) 31 0 k(3) 23 k(2) 11 +k(3) 22 0 k(2) 12 +k(3) 21 k(2) 13 k(1) 21 0 k(1) 22 k (1) 23 0 k(1) 31 +k(3) 13 k(2) 21 +k(3) 12 k (1) 32 k (1) 33 +k (2) 22 +k (3) 11 k (2) 23 0 k(2) 31 0 k(2) 32 k(2) 熿 燀 燄 33 燅 81 第1章 有限单元法基本程式

题 19 由于节点3,4,5固定,因此只需给出与节点1,2有关的整体刚度矩阵 [1.4 0 -1 -0.27 l41 0 1.4-0.4 0.4 -1-0.41.8 0.6 -0.20.40.6 2.4 0 ④未知量计算 a=[u11u2 Jr=是D.53590.52921.5748 -0.2772]1 为求解单元应力,需据此形成单元节点位移向量。例如,对于单元(1),有 a=w110000r=2D.53590.5290000 单元应力为 cD=g[0.11030.55131.0566]J 1.6结 语 从物理角度看,有限单元法将连续体问题转化成了离散体问题:从数学角度 看,有限单元法将微分方程问题转化为代数方程问题。结果,无限自由度问题变 成了有限自由度问题。 本章基于虚位移原理推导了位移法有限元公式,关于虚位移原理的证明见 第2章。必须指出,单元刚度方程(1.17)、单元刚度矩阵(1.18)、体力等效节点 荷载(1.19)、面力等效节点荷载(1.20)以及整体刚度方程(1.21)均具有普遍性。 在第2章中,将根据势能变分原理重新推导它们,以加深对有限单元法基本原理 的理解。 习题 1.1有限单元法中“离散”的含义是什么?有限单元法是如何将具有无限自由 度的连续介质问题转变成有限自由度问题的?位移有限单元法的标准化 程式是怎样的? 1.2什么叫做节点力和节点荷载?两者有什么不同?为什么应该保留节点力 的概念? 1.3单元刚度矩阵和整体刚度矩阵各有哪些性质?单元刚度系数和整体刚度 系数的物理意义是什么?两者有何区别? 1.4如图所示的有限元网格中,节点应如何编号,以使得整体刚度矩阵的半带
由于节点3,4,5固定,因此只需给出与节点1,2有关的整体刚度矩阵。 Et 192× 14 0 -1 -02 0 14 -04 04 -1 -04 18 06 熿 燀 燄 -02 04 06 24燅 u1 v1 u2 v 烅 烄 烆 烍 烌 2烎 =qt烅 烄 烆 烍 烌 烎 1 0 0 0 ④未知量计算 a=[u1 v1 u2 v2]T=q E [25359 05292 15748 -02772]T 为求解单元应力,需据此形成单元节点位移向量。例如,对于单元(1),有 a(1) =[u1 v1 0 0 0 0]T=q E [25359 05292 0 0 0 0]T 单元应力为 σ(1) =q[01103 05513 10566]T 16 结 语 从物理角度看,有限单元法将连续体问题转化成了离散体问题;从数学角度 看,有限单元法将微分方程问题转化为代数方程问题。结果,无限自由度问题变 成了有限自由度问题。 本章基于虚位移原理推导了位移法有限元公式,关于虚位移原理的证明见 第2章。必须指出,单元刚度方程(117)、单元刚度矩阵(118)、体力等效节点 荷载(119)、面力等效节点荷载(120)以及整体刚度方程(121)均具有普遍性。 在第2章中,将根据势能变分原理重新推导它们,以加深对有限单元法基本原理 的理解。 习 题 11 有限单元法中“离散”的含义是什么?有限单元法是如何将具有无限自由 度的连续介质问题转变成有限自由度问题的?位移有限单元法的标准化 程式是怎样的? 12 什么叫做节点力和节点荷载?两者有什么不同?为什么应该保留节点力 的概念? 13 单元刚度矩阵和整体刚度矩阵各有哪些性质?单元刚度系数和整体刚度 系数的物理意义是什么?两者有何区别? 14 如图所示的有限元网格中,节点应如何编号,以使得整体刚度矩阵的半带 习 题 91
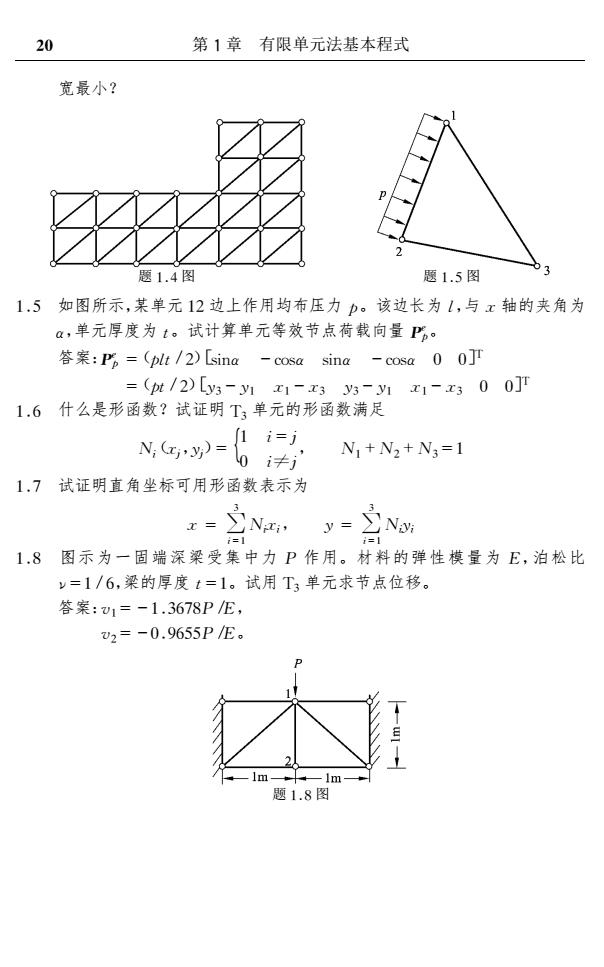
20 第1章有限单元法基本程式 宽最小? 题1.4图 题1.5图 1.5如图所示,某单元12边上作用均布压力p。该边长为1,与x轴的夹角为 a,单元厚度为t。试计算单元等效节点荷载向量P。 答案:P。=(plt/2)[sina -cosa sina-cosa 00 =t/2)[y3-Mx1-x33-yx1-x300] 1.6什么是形函数?试证明T;单元的形函数满足 1 i=j N,Gy)=0i≠ N1+N2+N3=1 1.7试证明直角坐标可用形函数表示为 y-No 1.8图示为一固端深梁受集中力P作用。材料的弹性模量为E,泊松比 y=1/6,梁的厚度t=1。试用T3单元求节点位移。 答案:v1=-1.3678P/E, v2=-0.9655PE。 题1.8图
宽最小? 题14图 题15图 15 如图所示,某单元12边上作用均布压力p。该边长为l,与x轴的夹角为 α,单元厚度为t。试计算单元等效节点荷载向量Pe p。 答案:Pe p =(plt/2)[sinα -cosα sinα -cosα 0 0]T =(pt/2)[y3-y1 x1-x3 y3-y1 x1-x3 0 0]T 16 什么是形函数?试证明T3单元的形函数满足 Ni (xj,yj)= 1 i=j {0 i≠j , N1+N2+N3=1 17 试证明直角坐标可用形函数表示为 x = ∑ 3 i=1 Nixi, y= ∑ 3 i=1 Niyi 18 图示为一固端深梁受集中力 P 作用。材料的弹性模量为 E,泊松比 ν=1/6,梁的厚度t=1。试用T3单元求节点位移。 答案:v1=-13678P/E, v2=-09655P/E。 题18图 02 第1章 有限单元法基本程式

第2章 有限单元法基本原理 结构分析是有限单元法最早、也是最广泛应用的领域。第1章以弹性力学 平面问题为例,阐释了有限单元法的基本内容。这样的介绍具有直观性,但缺乏 系统性和深刻性。为加深对有限单元法的理解,本章将系统而深入地阐述有限 单元法的基本原理,内容包括:①)介绍定解问题的微分方程提法:2)根据微分 方程的等效积分形式,推导第1章中未加证明而应用的虚位移原理及势能变分 原理,从而建立定解问题的泛函变分提法:3)基于势能变分原理推导位移有限 单元法的普遍公式,并对位移有限元解的性质和收敛性作简要说明:(4)基于余 能变分原理推导应力有限单元法的基本公式。 在本章的阐述中,仍以结构分析课题为例,但所有方面的论述均以一般性说 明为先导。 2.1微分方程提法 在物理或工程问题中,位移、应力、温度、电流等物理量称为场变量,它们在 一定区域内满足某些控制方程:在域边界上满足给定的边界条件,有时还有初始 条件,它们统称为定解条件:控制方程和定解条件构成所谓定解问题的微分方程 或数学模型,这种以微分方程形式提出问题的方法称为定解问题的微分方程提 法。 为了获得数学模型,必须引入某些前提假设以建构几何模型、物理模型或力 学模型等,它们统称为分析模型。本节首先简要介绍分析模型的概念,然后给出 定解问题微分方程提法的一般形式,最后列出弹性力学问题的微分方程。 2.1.1结构分析模型 对任何复杂事物的研究,出发点都是对事物进行逼真而又可行的理想化以 建构分析模型:而结果的可靠性和实用价值主要取决于确立模型时对各种控制 条件和参数的正确反映
第 2章 有限单元法基本原理 结构分析是有限单元法最早、也是最广泛应用的领域。第1章以弹性力学 平面问题为例,阐释了有限单元法的基本内容。这样的介绍具有直观性,但缺乏 系统性和深刻性。为加深对有限单元法的理解,本章将系统而深入地阐述有限 单元法的基本原理,内容包括:(1)介绍定解问题的微分方程提法;(2)根据微分 方程的等效积分形式,推导第1章中未加证明而应用的虚位移原理及势能变分 原理,从而建立定解问题的泛函变分提法;(3)基于势能变分原理推导位移有限 单元法的普遍公式,并对位移有限元解的性质和收敛性作简要说明;(4)基于余 能变分原理推导应力有限单元法的基本公式。 在本章的阐述中,仍以结构分析课题为例,但所有方面的论述均以一般性说 明为先导。 21 微分方程提法 在物理或工程问题中,位移、应力、温度、电流等物理量称为场变量,它们在 一定区域内满足某些控制方程;在域边界上满足给定的边界条件,有时还有初始 条件,它们统称为定解条件;控制方程和定解条件构成所谓定解问题的微分方程 或数学模型,这种以微分方程形式提出问题的方法称为定解问题的微分方程提 法。 为了获得数学模型,必须引入某些前提假设以建构几何模型、物理模型或力 学模型等,它们统称为分析模型。本节首先简要介绍分析模型的概念,然后给出 定解问题微分方程提法的一般形式,最后列出弹性力学问题的微分方程。 211 结构分析模型 对任何复杂事物的研究,出发点都是对事物进行逼真而又可行的理想化以 建构分析模型;而结果的可靠性和实用价值主要取决于确立模型时对各种控制 条件和参数的正确反映

22 第2章有限单元法基本原理 何谓模型?待分析的事物称为原型,其理想化的替代物就是模型。任何模 型都是为了某种特定目的而将原型的某些特征信息简缩、提炼而构造出来的。 原型有各方面的因素和各种层次的特征,而模型只要求反映与某种目的有关的 那些因素和层次。模型成功的关键是必须反映原型事物的主要属性和特征,而 什么是主要属性和特征则与我们所关注的问题有关(文献83)。 从本质上讲,有限单元法是求解微分方程的数值方法,即在物理或工程问题 的数学模型之基础上进行近似计算。因此,有限元计算的精度并不意味着实际 问题求解的精度。在采用有限单元法解题时,必须时刻牢记:问题的分析模型具 有根本的重要性。 现以结构分析问题为例,说明分析模型的基本概念。结构设计的核心任务 在于求解结构在外部荷载作用下产生的应力和变形。这些荷载效应取决于结构 类型、几何特征、材料性能、荷载条件等因素。在结构分析中,用于代替实际结构 并能反映结构主要受力和变形特点的理想模型称为结构分析模型,主要有几何 模型、力学模型、数学模型等。 从广义上理解,“结构”包括各种建筑结构、车身骨架、飞机机身、船舶结构 机械设备、堤坝边坡、建筑地基、洞室围岩等各种物体。任何结构及其构件都是 三维实体,但是在结构分析中,对某些特殊结构可以做出简化处理,并使得分析 更加有效。根据这种原则,人们将常见的结构分为杆系结构、薄壁结构和实体结 构(图2.1)。杆系结构就是若干个杆件通过若干个节点相互联结而组成的结构 体系。杆件的特点是横截面尺寸远比其杆长小得多。薄壁结构是厚度远小于其 他两个尺度的结构。如果结构的三个方向上尺度大约为同一量级,则称为实体 结构。在结构的几何与力学模型中,还需对结构的空间形式(平面结构、轴对称 结构、空间结构)、构件之间的连接形式(铰接、刚接或半刚接)、构件力学作用形 式(拉压、弯曲、扭转)等做出抽象。 (@)杆系结构 图2.10著嚮镬整 (©)薄壁结构 数学模型主要是指基于力学模型得到的控制方程,其是否符合实际关键在 于力学模型中引入的基本假定。例如,结构变形属于小变形还是大变形:材料是 线性弹性的还是非线性的。这些力学假定将反映到控制方程中,例如在线性弹 性小变形假设下,几何方程和本构方程都将是线性的
何谓模型?待分析的事物称为原型,其理想化的替代物就是模型。任何模 型都是为了某种特定目的而将原型的某些特征信息简缩、提炼而构造出来的。 原型有各方面的因素和各种层次的特征,而模型只要求反映与某种目的有关的 那些因素和层次。模型成功的关键是必须反映原型事物的主要属性和特征,而 什么是主要属性和特征则与我们所关注的问题有关(文献83)。 从本质上讲,有限单元法是求解微分方程的数值方法,即在物理或工程问题 的数学模型之基础上进行近似计算。因此,有限元计算的精度并不意味着实际 问题求解的精度。在采用有限单元法解题时,必须时刻牢记:问题的分析模型具 有根本的重要性。 现以结构分析问题为例,说明分析模型的基本概念。结构设计的核心任务 在于求解结构在外部荷载作用下产生的应力和变形。这些荷载效应取决于结构 类型、几何特征、材料性能、荷载条件等因素。在结构分析中,用于代替实际结构 并能反映结构主要受力和变形特点的理想模型称为结构分析模型,主要有几何 模型、力学模型、数学模型等。 从广义上理解,“结构”包括各种建筑结构、车身骨架、飞机机身、船舶结构、 机械设备、堤坝边坡、建筑地基、洞室围岩等各种物体。任何结构及其构件都是 三维实体,但是在结构分析中,对某些特殊结构可以做出简化处理,并使得分析 更加有效。根据这种原则,人们将常见的结构分为杆系结构、薄壁结构和实体结 构(图21)。杆系结构就是若干个杆件通过若干个节点相互联结而组成的结构 体系。杆件的特点是横截面尺寸远比其杆长小得多。薄壁结构是厚度远小于其 他两个尺度的结构。如果结构的三个方向上尺度大约为同一量级,则称为实体 结构。在结构的几何与力学模型中,还需对结构的空间形式(平面结构、轴对称 结构、空间结构)、构件之间的连接形式(铰接、刚接或半刚接)、构件力学作用形 式(拉压、弯曲、扭转)等做出抽象。 图21 结构模型 数学模型主要是指基于力学模型得到的控制方程,其是否符合实际关键在 于力学模型中引入的基本假定。例如,结构变形属于小变形还是大变形;材料是 线性弹性的还是非线性的。这些力学假定将反映到控制方程中,例如在线性弹 性小变形假设下,几何方程和本构方程都将是线性的。 22 第2章 有限单元法基本原理