
4 有限单元法 第15章几何非线性问题 270 15.1变形和位移 (270 15.2应变度量… (276) 15.3应力度量… 280) 15.4本构方程… 283) 15.5平衡方程 (286) 15.6微分方程弱形式… 286) 15.7有限元离散方程… 289) 15.8结语 (296) 习 题… 296) 第16章边界非线性问题 298) 16.1接触问题定义 298) 16.2接触分析原理… 303) 16.3接触问题算法… 304) 16.4结语… 308) 习 题… 309) 第17章有限单元法旁系发展 310) 17.1边界单元法 310) 17.2有限条法 314) 17.3有限元线法 319 17.4 无网格法· 322 17.5结语 326 习 题 (326 参考文献 327)
第15章 几何非线性问题 (270)………………………………………………… 151 变形和位移 (270)………………………………………………………… 152 应变度量 (276)…………………………………………………………… 153 应力度量 (280)…………………………………………………………… 154 本构方程 (283)…………………………………………………………… 155 平衡方程 (286)…………………………………………………………… 156 微分方程弱形式 (286)…………………………………………………… 157 有限元离散方程 (289)…………………………………………………… 158 结语 (296)………………………………………………………………… 习 题 (296)…………………………………………………………………… 第16章 边界非线性问题 (298)………………………………………………… 161 接触问题定义 (298)……………………………………………………… 162 接触分析原理 (303)……………………………………………………… 163 接触问题算法 (304)……………………………………………………… 164 结语 (308)………………………………………………………………… 习 题 (309)…………………………………………………………………… 第17章 有限单元法旁系发展 (310)…………………………………………… 171 边界单元法 (310)………………………………………………………… 172 有限条法 (314)…………………………………………………………… 173 有限元线法 (319)………………………………………………………… 174 无网格法 (322)…………………………………………………………… 175 结语 (326)………………………………………………………………… 习 题 (326)…………………………………………………………………… 参考文献 (327)……………………………………………………………………… 4 有限单元法

主要符号 主要符号 单元面积 A 平面问题或板弯曲问题中的单元面积域 a 单元节点位移向量 整体节点位移向量 B,Bi 单元应变矩阵及其子矩阵 Bb Bbi 板单元弯曲应变矩阵及其子矩阵 B Bsi 板单元剪切应变矩阵及其子矩阵 C 阻尼矩阵或柔度矩阵 弹性矩阵 弹性模量 体力向量 G 剪切模量 J,J Jacobi矩阵及其行列式 K,K 单元刚度矩阵,整体刚度矩阵 Li 三角形单元的面积坐标 M 弯矩 M 质量矩阵或薄板弯曲中力矩组成的广义应力向量 M,My Mo 板弯曲问题中垂直x轴和y轴的截面上单位长度 的弯矩及扭矩 N,Ni 单元形函数矩阵,节点;的形函数 P,P 整体荷载向量,单元等效节点荷载向量 面力向量 转换矩阵 单元厚度 单元位移向量 u,v,w 位移向量的分量,表示x,y,之方向的位移 应变向量 6 应力向量 方向余弦矩阵
主 要 符 号 A 单元面积 Ae 平面问题或板弯曲问题中的单元面积域 ae 单元节点位移向量 a 整体节点位移向量 B,Bi 单元应变矩阵及其子矩阵 Bb,Bbi 板单元弯曲应变矩阵及其子矩阵 Bs,Bsi 板单元剪切应变矩阵及其子矩阵 C 阻尼矩阵或柔度矩阵 D 弹性矩阵 E 弹性模量 f 体力向量 G 剪切模量 J,J Jacobi矩阵及其行列式 Ke,K 单元刚度矩阵,整体刚度矩阵 Li 三角形单元的面积坐标 M 弯矩 M 质量矩阵或薄板弯曲中力矩组成的广义应力向量 Mx,My,Mxy 板弯曲问题中垂直x轴和y轴的截面上单位长度 的弯矩及扭矩 N,Ni 单元形函数矩阵,节点i的形函数 P,Pe 整体荷载向量,单元等效节点荷载向量 p 面力向量 T 转换矩阵 t 单元厚度 u 单元位移向量 u,v,w 位移向量的分量,表示x,y,z方向的位移 ε 应变向量 σ 应力向量 方向余弦矩阵 主要符号 1

2 有限单元法 0,0a,0 梁、板、壳法线转角 5,7,5 单元局部坐标或等参坐标 Ⅱc,Ⅱm 余能泛函及修正余能泛函 Lp,Ⅱme 势能泛函及修正势能泛函 2,T 求解域及其边界
θ , θxi , θyi 梁、板、壳法线转角 ξ , η , ζ 单元局部坐标或等参坐标 Πc , Π m c 余能泛函及修正余能泛函 Πp , Π m p 势能泛函及修正势能泛函 Ω , Γ 求解域及其边界 2 有限单元法

第1章 有限单元法基本程式 有限单元法(Finite Element Method,简称FEMD是一种求解微分方程的近 似方法,起点自然是针对物理或工程问题建立起来的微分方程,包括控制方程和 边界条件:而有限元分析程式早己标准化,典型步骤包括结构或区域离散、单元 分析、整体分析和数值求解。 本章以弹性力学平面问题为例,阐述有限单元法的基本概念与程式。采用 有限单元法求解平面问题不仅简单,而且具有典型性。掌握了平面问题的有限 元分析方法,就可以很容易地推广到其他问题中去。 1.1弹性力学平面问题 1.1.1基本概念 平面问题是指这样一些问题,其结构尺寸及荷载分布沿某个方向(通常取为 之轴)不变,且具有特殊的边界条件。这样,结构内部的应力和应变就与之坐标 无关,而只是x,y坐标的函数。平面问题分为两种,即平面应力问题和平面应 变问题。 1)平面应力问题 如果在结构内部只存在xy平面内的三个应力分量。,o,c,而另外三个 应力分量=xa=x=0,则称为平面应力问题。例如,只承受纵向面内荷载 的薄板就可近似地视为这种问题(图1.1):由于板很薄,故可认为应力和应变 与之坐标无关。再注意到平板两面上的a,=x=t=0,便可近似地认为这些 应力分量在板内也为零。对于各向同性线性弹性介质,根据广义Hooke定律, 平面应力问题中的Yz和Y,显然为零,而e:由下式确定 ,=-(+) 1.1) 其中,E为弹性模量:v为泊松比
第 1章 有限单元法基本程式 有限单元法(FiniteElementMethod,简称FEM)是一种求解微分方程的近 似方法,起点自然是针对物理或工程问题建立起来的微分方程,包括控制方程和 边界条件;而有限元分析程式早已标准化,典型步骤包括结构或区域离散、单元 分析、整体分析和数值求解。 本章以弹性力学平面问题为例,阐述有限单元法的基本概念与程式。采用 有限单元法求解平面问题不仅简单,而且具有典型性。掌握了平面问题的有限 元分析方法,就可以很容易地推广到其他问题中去。 11 弹性力学平面问题 111 基本概念 平面问题是指这样一些问题,其结构尺寸及荷载分布沿某个方向(通常取为 z轴)不变,且具有特殊的边界条件。这样,结构内部的应力和应变就与z坐标 无关,而只是x,y坐标的函数。平面问题分为两种,即平面应力问题和平面应 变问题。 (1)平面应力问题 如果在结构内部只存在xy平面内的三个应力分量σx,σy,τxy,而另外三个 应力分量σz=τzx=τzy=0,则称为平面应力问题。例如,只承受纵向面内荷载 的薄板就可近似地视为这种问题(图11a):由于板很薄,故可认为应力和应变 与z坐标无关。再注意到平板两面上的σz=τzx=τzy=0,便可近似地认为这些 应力分量在板内也为零。对于各向同性线性弹性介质,根据广义 Hooke定律, 平面应力问题中的γzx和γzy显然为零,而εz由下式确定 εz=-ν E( ) σx+σy (11) 其中,E 为弹性模量;ν为泊松比
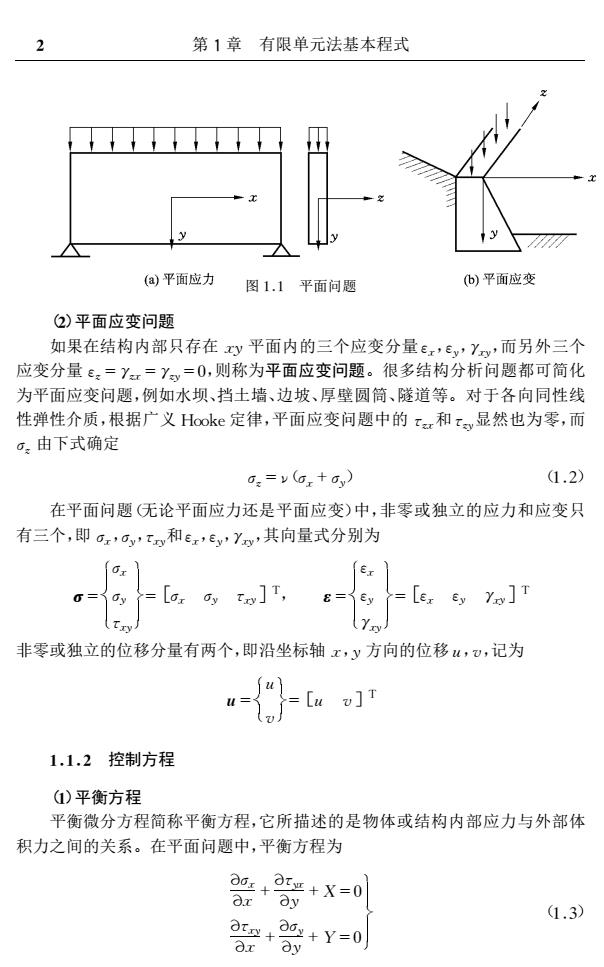
第1章有限单元法基本程式 (a)平面应力 图1.1平面问题 )平面应变 )平面应变问题 如果在结构内部只存在xy平面内的三个应变分量e,Ev,Y,而另外三个 应变分量:=Yx=Y=0,则称为平面应变问题。很多结构分析问题都可简化 为平面应变问题,例如水坝、挡土墙、边坡、厚壁圆筒、隧道等。对于各向同性线 性弹性介质,根据广义Hooke定律,平面应变问题中的x和x,显然也为零,而 o:由下式确定 as=y (a,+ay) 1.2) 在平面问题无论平面应力还是平面应变)中,非零或独立的应力和应变只 有三个,即a,oy,x和ex,y,Y,其向量式分别为 Er ay to]T, E=y =Ler Ey]T 非零或独立的位移分量有两个,即沿坐标轴x,y方向的位移,o,记为 u =[u v]T 1.1.2控制方程 ①)平衡方程 平衡微分方程简称平衡方程,它所描述的是物体或结构内部应力与外部体 积力之间的关系。在平面问题中,平衡方程为 ++X=0】 .3) 2+0+y-0
图11 平面问题 (2)平面应变问题 如果在结构内部只存在xy平面内的三个应变分量εx,εy,γxy,而另外三个 应变分量εz=γzx=γzy=0,则称为平面应变问题。很多结构分析问题都可简化 为平面应变问题,例如水坝、挡土墙、边坡、厚壁圆筒、隧道等。对于各向同性线 性弹性介质,根据广义 Hooke定律,平面应变问题中的τzx和τzy显然也为零,而 σz由下式确定 σz=ν(σx+σy) (12) 在平面问题(无论平面应力还是平面应变)中,非零或独立的应力和应变只 有三个,即σx,σy,τxy和εx,εy,γxy,其向量式分别为 σ= σx σy τx 烅 烄 烆 烍 烌 y烎 =[ ] σx σy τxy T, ε= εx εy γx 烅 烄 烆 烍 烌 y烎 =[ ] εx εy γxy T 非零或独立的位移分量有两个,即沿坐标轴x,y方向的位移u,v,记为 u= u 烅 烄 烆 烍 烌 v烎 =[ ] u v T 112 控制方程 (1)平衡方程 平衡微分方程简称平衡方程,它所描述的是物体或结构内部应力与外部体 积力之间的关系。在平面问题中,平衡方程为 σx x+ τyx y +X=0 τxy x + σy y +Y 烍 烌 =0烎 (13) 2 第1章 有限单元法基本程式