
导航 2.空间向量的数量积 (1)定义:已知两个非零向量a,b,则 叫做a,b 的数量积,记作ab.即ab= 特别地,零向量 与任意向量的数量积为 (2)性质: ①a⊥b台 ②aa=a acos<a,a>=
导航 2.空间向量的数量积 (1)定义:已知两个非零向量a,b,则 |a||b|cos<a,b> 叫做a,b 的数量积,记作a·b.即a·b= |a||b|cos<a,b> .特别地,零向量 与任意向量的数量积为 0 . (2)性质: ①a⊥b⇔ a·b=0 ; ②a·a=|a||a|cos<a,a>= |a| 2

导航 (3)运算律: ①(2a)b=(ab),λ∈R; ②ab=ba(交换律); ③a(b+c)=ab+ac(分配律). 微思考数量积运算满足结合律吗? 提示:数量积运算不满足结合律 即(ab)c=a(bc)一般不成立
导航 (3)运算律 : ① (λ a)· b = λ ( a · b), λ ∈R; ② a · b = b · a (交换律); ③ a·( b + c)= a · b + a · c (分配律 ). 微思考数量积运算满足结合律吗 ? 提示 :数量积运算不满足结合律 , 即 ( a · b)· c = a·( b · c )一般不成立
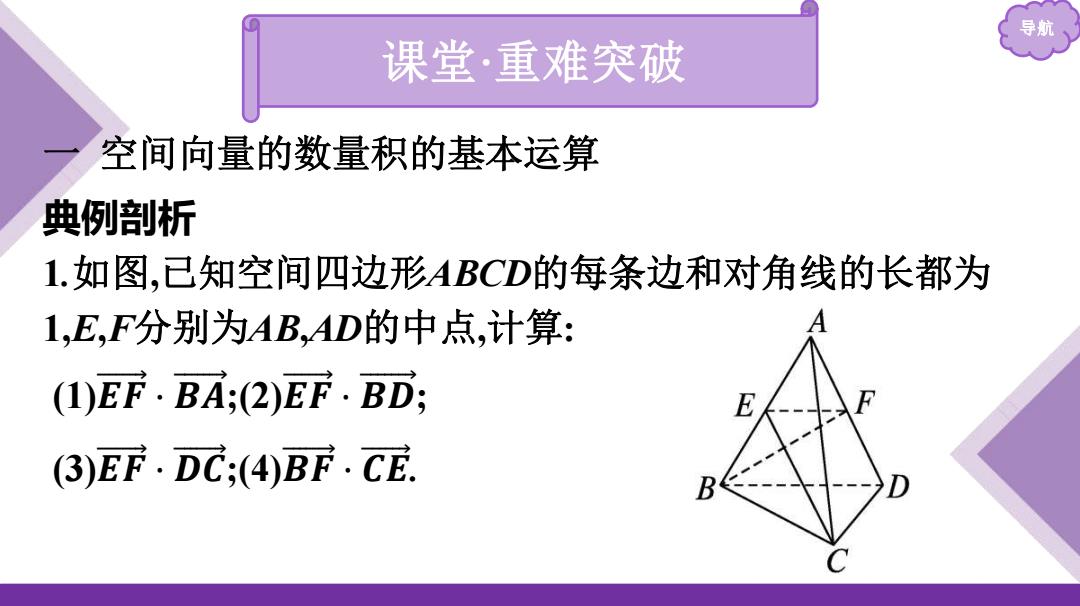
导航 课堂·重难突破 空间向量的数量积的基本运算 典例剖析 1.如图,已知空间四边形ABCD的每条边和对角线的长都为 1,E,F分别为AB,AD的中点,计算: (1)EF.BA;(2)EF.BD; ()EF.DC;(4)BF.CE
导航 课堂·重难突破 一 空间向量的数量积的基本运算 典例剖析 1.如图,已知空间四边形ABCD的每条边和对角线的长都为 1,E,F分别为AB,AD的中点,计算: (1)𝑬 𝑭 ·𝑩 𝑨 ;(2)𝑬 𝑭 ·𝑩 𝑫 ; (3)𝑬 𝑭 ·𝑫 𝑪 ;(4)𝑩 𝑭 ·𝑪 𝑬

导航 解:(EF.BA=2BD.BA BDBAl-cOs<BD,BA> x1x1x0s60° 故EF·BA=
导航 解:(1)𝑬 𝑭 ·𝑩 𝑨 = 𝟏 𝟐 𝑩 𝑫 ·𝑩 𝑨 = 𝟏 𝟐 |𝑩 𝑫 |·|𝑩 𝑨 |·cos<𝑩 𝑫 , 𝑩 𝑨 > = 𝟏 𝟐 ×1×1×cos 60°= 𝟏 𝟒 , 故𝑬 𝑭 ·𝑩 𝑨 = 𝟏 𝟒
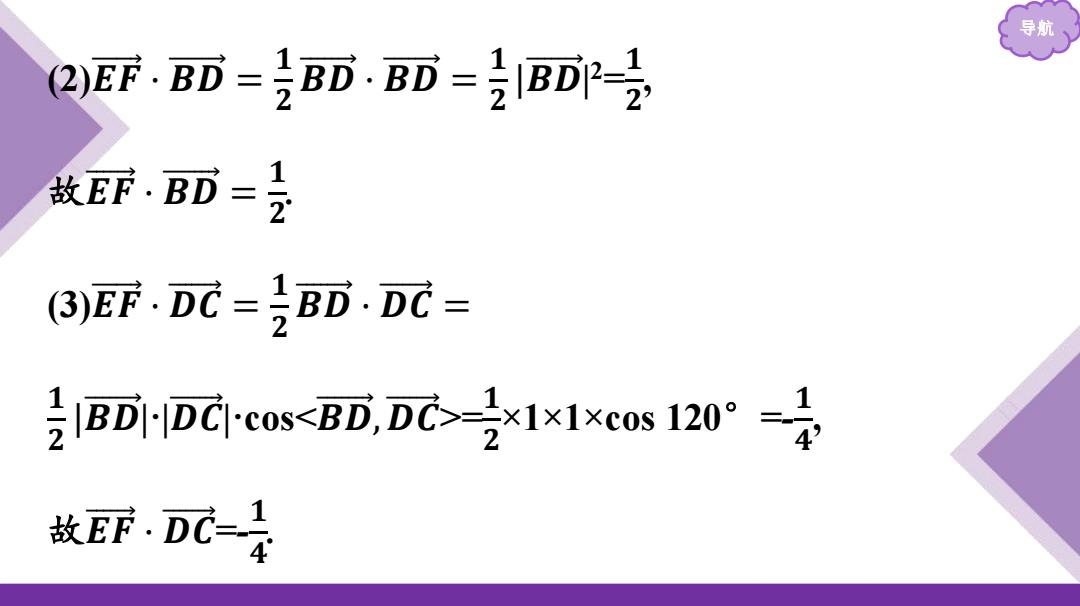
导航 2F.BD=2BD.B而-2BD-2 故EF.BD=2 (3)EF.DC=BD.DC= 2IBD1-DCrc0s<BD,DC1x1×c0s120°=} 故E耶DC-是
导航 (2)𝑬 𝑭 ·𝑩 𝑫 = 𝟏 𝟐 𝑩 𝑫 ·𝑩 𝑫 = 𝟏 𝟐 |𝑩 𝑫 | 2 = 𝟏 𝟐 , 故𝑬 𝑭 ·𝑩 𝑫 = 𝟏 𝟐 . (3)𝑬 𝑭 ·𝑫 𝑪 = 𝟏 𝟐 𝑩 𝑫 ·𝑫 𝑪 = 𝟏 𝟐 |𝑩 𝑫 |·|𝑫 𝑪 |·cos<𝑩 𝑫 ,𝑫 𝑪 >= 𝟏 𝟐 ×1×1×cos 120°=- 𝟏 𝟒 , 故𝑬 𝑭 ·𝑫 𝑪 =- 𝟏 𝟒