
线性代教敖程■ 第三章矩阵的初等变换与线性方程组 23:45 6 3-2 例2求矩阵B 1-25 0004-3 的秩 0000 0 解:B是一个行阶梯形矩阵,其非零行郁行, B的所有4阶子式全为零 2-13 而03-2≠0,.R(B)=3. 004 第6项
线性代数教程 线性代数小组 第三章 矩阵的初等变换与线性方程组 23:45 第6页 例2 . 0 0 0 0 0 0 0 0 4 3 0 3 1 2 5 2 1 0 3 2 求矩阵 的秩 − − − − B = 解 B是一个行阶梯形矩阵,其非零行有3行, B的所有 4阶子式全为零. 0, 0 0 4 0 3 2 2 1 3 − − 而 R(B) = 3

线性代数赦程第三章矩阵的初等变换与线性方程组 2345 请回答: 设R4)=r,那么 )所有的r阶子式都为0,对吗? 错! (2)所有的+1阶子式都为0,对吗? 对! 3)所有的+2阶子式都为0,对吗? 对! (4)所有的+3阶子式都为0,对吗? 对! 第7页
线性代数教程 线性代数小组 第三章 矩阵的初等变换与线性方程组 23:45 第7页 请回答: 设R(A) = r,那么 (1)所有的 r 阶子式都为0,对吗? (2)所有的 r+1 阶子式都为0,对吗? (3)所有的 r+2 阶子式都为0,对吗? (4)所有的 r+3 阶子式都为0,对吗? . 错! 对! 对! 对!

线性代数敖程 第三章矩阵的初等变换与线性方程组 23:45 请回答: 设R()=r,那么 )有没有等于0的1阶子式? 有! (2)有没有等于0的r阶子式? 有! (3)有没有等于0的+1阶子式? 有!全是 第8项
线性代数教程 线性代数小组 第三章 矩阵的初等变换与线性方程组 23:45 第8页 请回答: 设R(A) = r,那么 (1)有没有等于0的 r-1 阶子式? (2)有没有等于0的 r 阶子式? . 有! 有! (3)有没有等于0的 r+1 阶子式? 有!全是

线性代数教程 第三章矩阵的初等变换与线性方程组 23.45 ”w期 求该矩阵的秩, 解 =2≠0,计算A的3阶子式, 13 -21323-221-22 02-1=0023D,-1300-13=0, -20 1 -205015-215 =0. ∴.R(A=2. 第9页
线性代数教程 线性代数小组 第三章 矩阵的初等变换与线性方程组 23:45 第9页 例3 已知 ,求该矩阵的秩. − − − = 2 0 1 5 0 2 1 3 1 3 2 2 A 2 0, 0 2 1 3 = 2 0 1 0 2 1 1 3 2 − − − 2 0 5 0 2 3 1 3 2 − 解 计算A的3阶子式, = 0, = 0, 0 1 5 2 1 3 3 2 2 − − 2 1 5 0 1 3 1 2 2 − − − = = 0, = 0, = = = 0. R(A) = 2
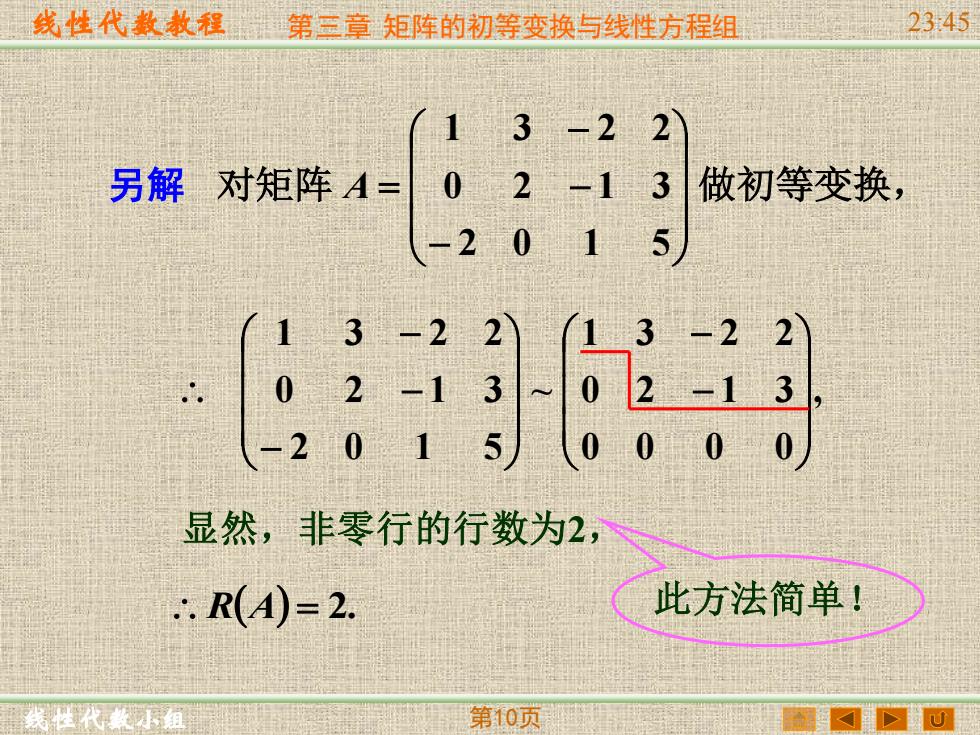
线性代数敖程 第三章矩阵的初等变换与线性方程组 23:45 13-22 另解对矩阵A02-13 做初等变换, -2015 13-2 02 0000 显然,非零行的行数为2, .R(A)=2. 此方法简单! 第10页
线性代数教程 线性代数小组 第三章 矩阵的初等变换与线性方程组 23:45 第10页 对矩阵 做初等变换, − − − = 2 0 1 5 0 2 1 3 1 3 2 2 另解 A , 0 0 0 0 0 2 1 3 1 3 2 2 ~ 2 0 1 5 0 2 1 3 1 3 2 2 − − − − − 显然,非零行的行数为2, R(A) = 2. 此方法简单!