
二、Jy=Asin(wx+p)+k(或y=Acos(wx+p)+k,A,0,p,k∈R且 A,0≠0)的图象 【问题思考】 1.填空:(1)用五点法”作y=Asin(wx+p)+k的图象时,令ωx+p 取的五个值依次为受-受, (2)通过变换由y=cosx的图象作y=Acos(wx+p)+k的图象时, 若平移的量为个单位,则为先 变换后 变换 2做一做:将=c0s(2x)的图象向_平移个单位,得到 y=c0s2x的图象
导航 二、y=Asin(ωx+φ)+k(或y=Acos(ωx+φ)+k,A,ω,φ,k∈R且 A,ω≠0)的图象 【问题思考】 1.填空:(1)用“五点法”作 y=Asin(ωx+φ)+k 的图象时,令 ωx+φ 取的五个值依次为 0 , 𝛑 𝟐 , π , 𝟑𝛑 𝟐 , 2π . (2)通过变换由 y=cos x 的图象作 y=Acos(ωx+φ)+k 的图象时, 若平移的量为 𝝋 𝝎 个单位,则为先周期变换后相位变换. 2.做一做:将 y=cos 𝟐𝒙- 𝛑 𝟔 的图象向左平移 𝛑 𝟏𝟐 个单位,得到 y=cos 2x 的图象

【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“V”,错误 的画“×” (1)函数y=tan-1有最小值无最大值.( (2)若函数-3cos(2ax+的周期为元,则=l.( (3)可以用“五点法”作函数y=V2cos(6元x+3)的简图.( (4)将y=sin(x+)的图象向左平移g个单位得到y=sinx的图 象(
导航 【思考辨析】 判断下列说法是否正确,正确的在它后面的括号里画“√”,错误 的画“×”. (1)函数 y=|tan x|-1 有最小值无最大值.( √ ) (2)若函数 y=3cos 𝟐𝒂𝒙 + 𝛑 𝟑 的周期为 π,则 a=1.( × ) (3)可以用“五点法”作函数 y=√𝟐cos(6πx+3)- 𝟏 𝟐 的简图.( √ ) (4)将 y=sin 𝒙 + 𝛑 𝟔 的图象向左平移𝛑 𝟔 个单位得到 y=sin x 的图 象.( × )

导期 课堂·重难突破 探究一作三角函数的图象 【例1】已知函数f)=V2sin(2ωx+)(o>0)的最小正周期 为元 (1)求ω的值;2)用“五点法”作出fx)的图象 分析:()利用T2求w的值;2)按“五点法”的作图步骤进行
导航 课堂·重难突破 探究一 作三角函数的图象 【例1】已知函数 (ω>0)的最小正周期 为π. (1)求ω的值;(2)用“五点法”作出f(x)的图象. f(x)=√𝟐sin 𝟐𝝎𝒙 + 𝛑 𝟒 分析:(1)利用 T=𝟐𝛑 𝝎 求 ω 的值;(2)按“五点法”的作图步骤进行

导航 解:20l ②)由(1加,w)=V2sin(2x+罩》, 列表: π 3π 5π 7π 8 8 8 8 8 2r+ π 3π 0 2元 4 2 怀 2 fx) 0 2 0 -V2 0
导航 解:(1)∵ 𝟐𝛑 𝟐𝝎 =π,∴ω=1. (2)由(1)知,f(x)=√𝟐sin 𝟐𝒙 + 𝛑 𝟒 , 列表: x - 𝝅 𝟖 𝝅 𝟖 𝟑𝝅 𝟖 𝟓𝝅 𝟖 𝟕𝝅 𝟖 2x+𝝅 𝟒 0 𝝅 𝟐 π 𝟑𝝅 𝟐 2π f(x) 0 √𝟐 0 -√𝟐 0
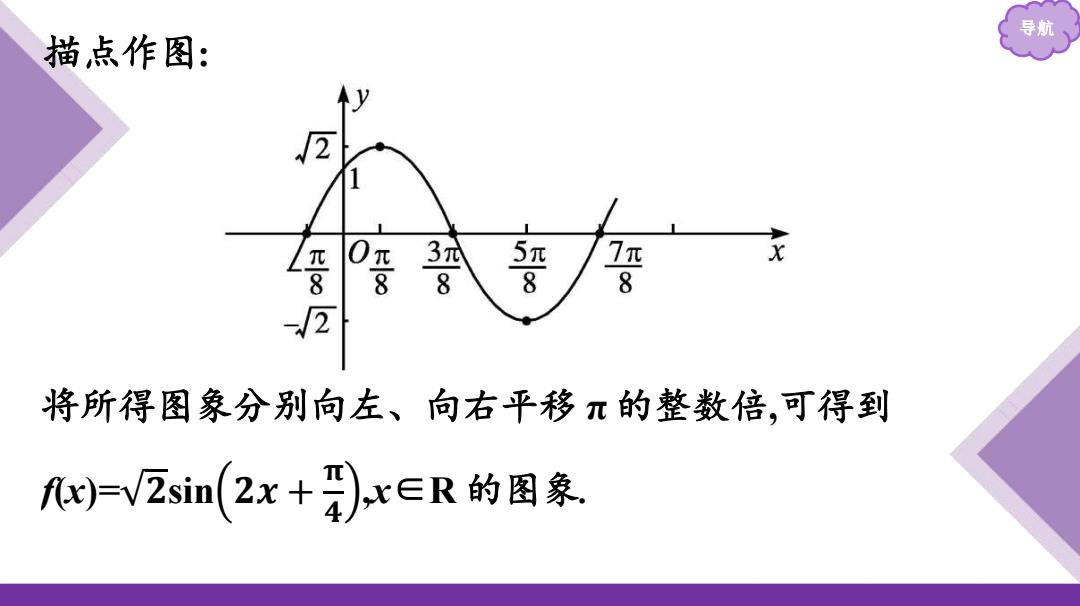
导航 描点作图: 2 3列 7π x 将所得图象分别向左、向右平移π的整数倍,可得到 )=V2sin(2x+),rx∈R的图象
导航 描点作图: 将所得图 象分别向左、向右平移 π 的整数倍,可得到 f(x)= √𝟐sin 𝟐 𝒙 + 𝛑𝟒 ,x ∈ R 的图 象