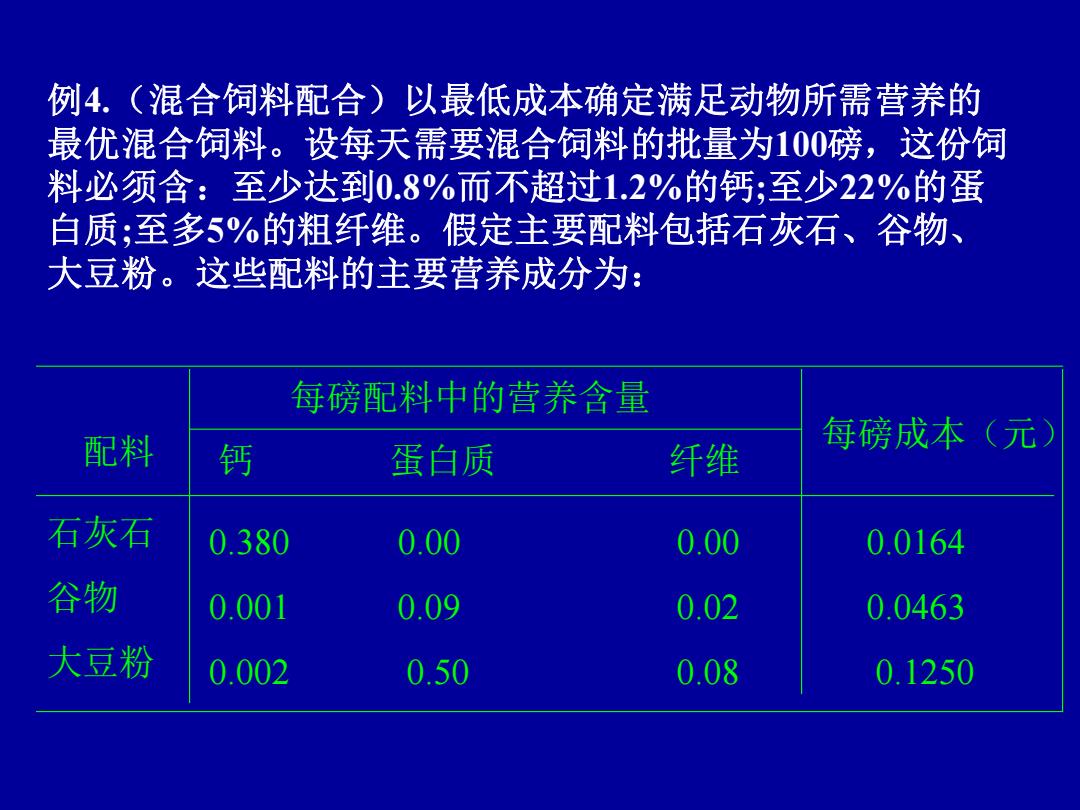
例4.(混合饲料配合)以最低成本确定满足动物所需营养的 最优混合饲料。设每天需要混合饲料的批量为100磅,这份饲 料必须含:至少达到0.8%而不超过1.2%的钙;至少22%的蛋 白质;至多5%的粗纤维。假定主要配料包括石灰石、谷物、 大豆粉。这些配料的主要营养成分为: 每磅配料中的营养含量 配料 每磅成本(元) 钙 蛋白质 纤维 石灰石 0.380 0.00 0.00 0.0164 谷物 0.001 0.09 0.02 0.0463 大豆粉 0.002 0.50 0.08 0.1250
配料 每磅配料中的营养含量 钙 蛋白质 纤维 每磅成本(元) 石灰石 谷物 大豆粉 0.380 0.00 0.00 0.001 0.09 0.02 0.002 0.50 0.08 0.0164 0.0463 0.1250 例4.(混合饲料配合)以最低成本确定满足动物所需营养的 最优混合饲料。设每天需要混合饲料的批量为100磅,这份饲 料必须含:至少达到0.8%而不超过1.2%的钙;至少22%的蛋 白质;至多5%的粗纤维。假定主要配料包括石灰石、谷物、 大豆粉。这些配料的主要营养成分为:

解:根据前面介绍的建模要素得出此问题的数学模型如下: 设X,X2,X3是生产100磅混合饲料所须的石灰石、谷物、大豆 粉的量(磅) minZ=0.0164x+0.0463x2+0.1250x3 S.t. x+x2+x3=100 0.380x+0.001x2+0.002x3≤0.012×100 0.380x+0.001x2+0.002x3≥0.008×100 0.09x2+0.50x3≥0.22×100 0.02x2+0.08x≤0.05×100 x≥0, x2≥0 X3≥0 注意单位统一
1 2 3 1 2 3 1 2 3 1 2 3 2 3 2 3 1 2 3 min 0.0164 0.0463 0.1250 . . 100 0.380 0.001 0.002 0.012 100 0.380 0.001 0.002 0.008 100 0.09 0.50 0.22 100 0.02 0.08 0.05 100 0, 0, 0 Z x x x s t x x x x x x x x x x x x x x x x = + + + + = + + + + + + 解:根据前面介绍的建模要素得出此问题的数学模型如下: 设 是生产100磅混合饲料所须的石灰石、谷物、大豆 粉的量(磅)。 1 2 3 x x x , , 注意单位统一
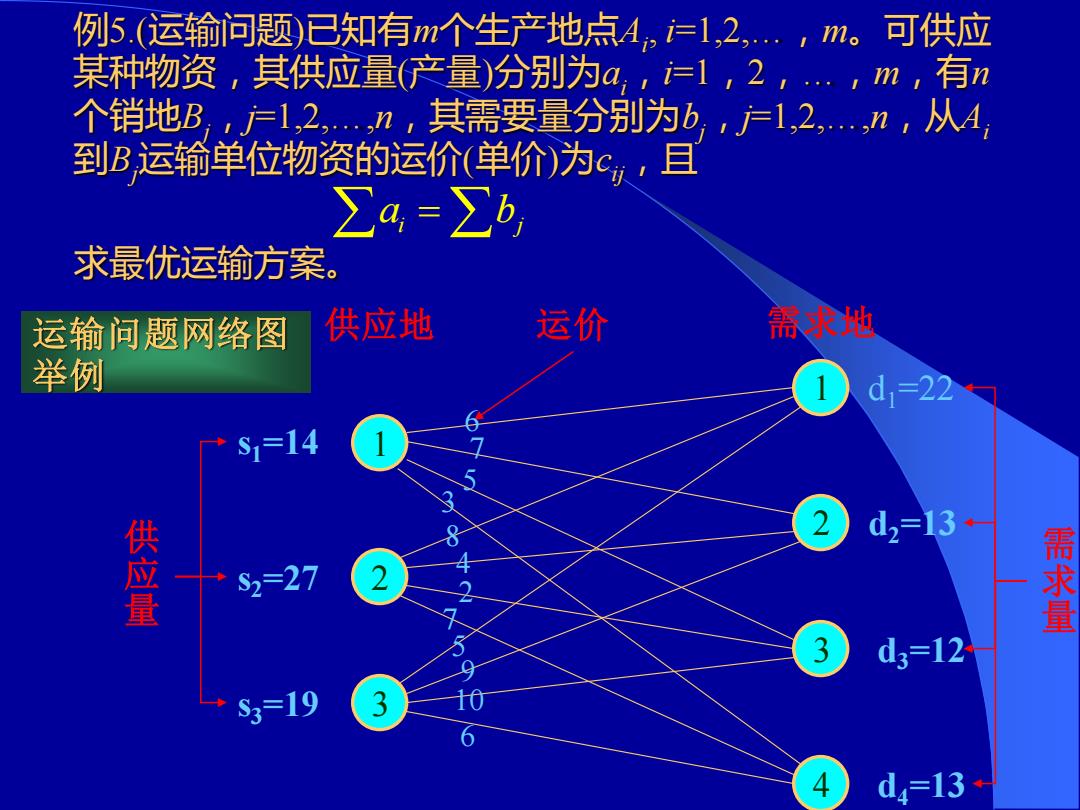
例5.(运输问题)已知有m个生产地点4,1,2,…,m。可供应 某种物资,其供应量(产量)分别为a,1,2,…,m,有n 个销地B,户1,2…,n,其需要量分别为b,户1,2,n,从4 到B运输单位物资的运价(单价)为c,,且 ∑a=∑b 求最优运输方案。 运输问题网络图 供应地 运价 举例 d1=22 S1=14 3 2 供应量 S2=27 84 d2=13 需求 又5906 3 d3=12 S3=19 3 4 d4=13
例5.(运输问题)已知有m个生产地点Ai , i=1,2,…,m。可供应 某种物资,其供应量(产量)分别为ai,i=1,2,…,m,有n 个销地Bj,j=1,2,…,n,其需要量分别为bj,j=1,2,…,n,从Ai 到Bj运输单位物资的运价(单价)为cij,且 求最优运输方案。 i j a b = 2 3 2 1 3 4 1 运输问题网络图 举例 s2=27 s3=19 d1=22 d2=13 d3=12 d4=13 s1=14 供 应 量 供应地 运价 需 求 量 需求地 6 7 5 3 8 4 2 7 5 9 10 6
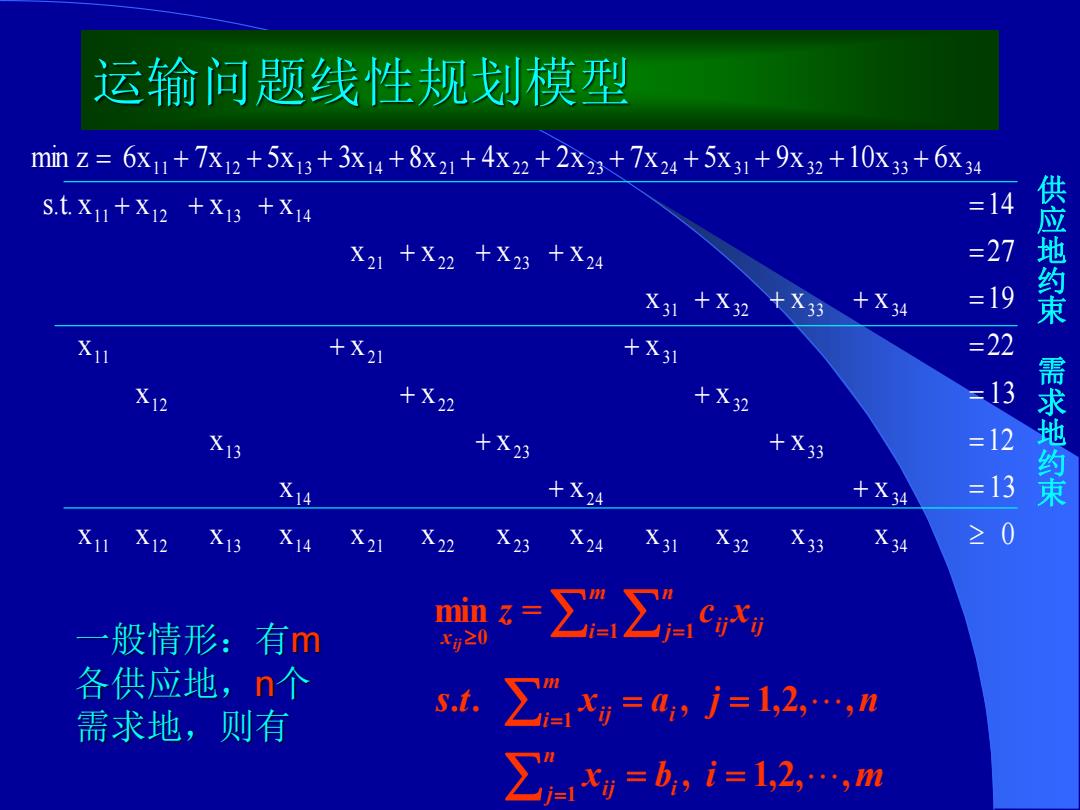
运输问题线性规划模型 mnZ=6x11+7x12+5x13+3x14+8x21+4x22+2X23+7x24+5x31+9x32+10x33+6x34 S.tX1u+X12+X13+X14 =14 X21+X22+X23+X24 =27 X31+X32+X3 +X34 =19 供应地约束 十X21 +X3到 =22 +X22 十X32 X13 十X3 十X33 =1 X14 十X24 +X34 16 需求地约束 X11X12X13X14X21X2X23 X24X31X2X3X34 ≥0 般情形:有m m-∑∑4c, 各供应地,n个 s.t. 需求地,则有 ∑xy=ayj=12,…,n ∑1x)=b,i=12,…,m
运输问题线性规划模型 x x x x x x x x x x x x 0 x x x 13 x x x 12 x x x 13 x x x 22 x x x x 19 x x x x 27 s.t. x x x x 14 min z 6x 7x 5x 3x 8x 4x 2x 7x 5x 9x 10x 6x 1 1 1 2 1 3 1 4 2 1 2 2 2 3 2 4 3 1 3 2 3 3 3 4 1 4 2 4 3 4 1 3 2 3 3 3 1 2 2 2 3 2 1 1 2 1 3 1 3 1 3 2 3 3 3 4 2 1 2 2 2 3 2 4 1 1 1 2 1 3 1 4 1 1 1 2 1 3 1 4 2 1 2 2 2 3 2 4 3 1 3 2 3 3 3 4 + + = + + = + + = + + = + + + = + + + = + + + = = + + + + + + + + + + + 供应地约束需求地约束 一般情形:有 m 各供应地, n 个 需求地,则有 x b i m s t x a j n z c x i nj i j i mi i j mi nj i j i j xij , 1,2, , . . , 1,2, , min = 11 1 1 0 = = = = == = =
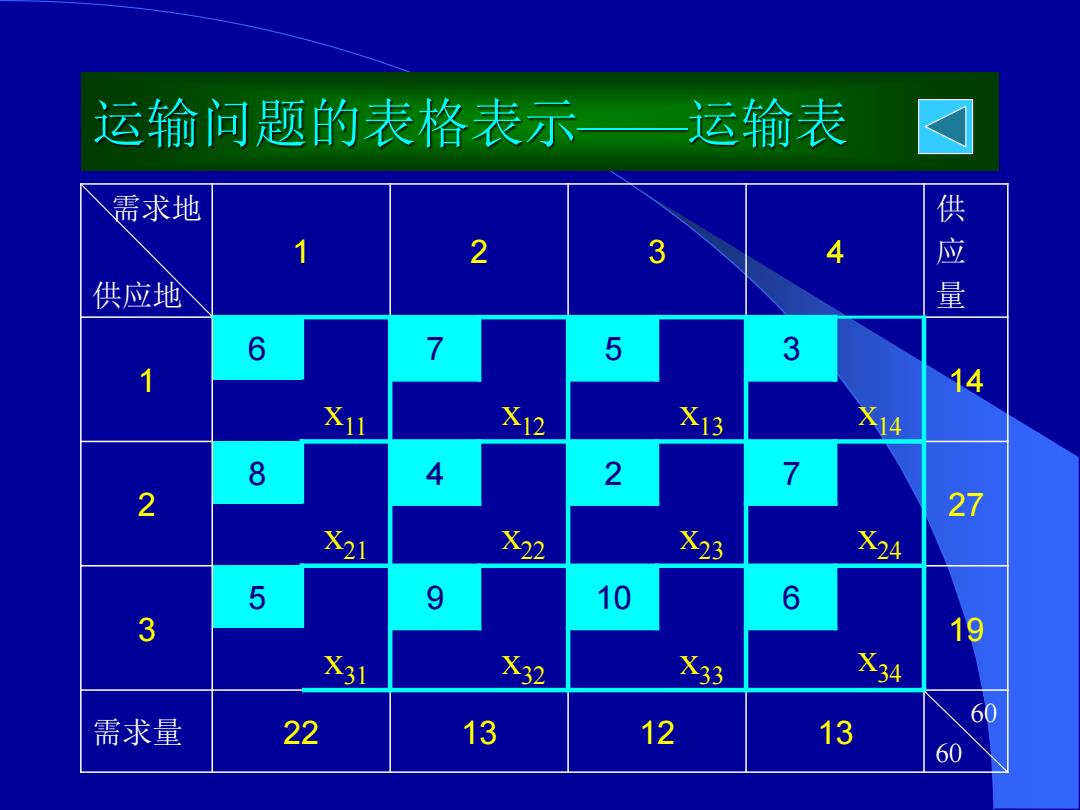
运输问题的表格表示一运输表 需求地 1 2 3 4 供应地 供应量 6 7 5 3 1 4 Xj1 X12 X13 X14 8 4 2 2 27 X21 X22 X23 X24 5 9 10 6 3 19 X31 X32 X33 X34 60 需求量 22 13 12 13 60
运输问题的表格表示——运输表 需求地 供应地 1 2 3 4 供 应 量 1 6 7 5 3 14 x11 x12 x13 x14 2 8 4 2 7 27 x21 x22 x23 x24 3 5 9 10 6 19 x31 x32 x33 x34 需求量 22 13 12 13 60 60