《复变函数与积分变换》课程教学资源（PPT课件）第六章 共形映射 6.3 第三节 唯一决定分式线性映射的条件

复变函数结论：在分式线性映射下，C的内部不是映射成C'的内部便映射成C'的外部判别方法：方法1 在分式线性映射下,如果在圆周C内任取一点Zo,若 Z的象在C'内部,则C的内部就映为C'的内部;若Z的象在C'外部,则C的内部就映为C'的外部U

6 结论: 在分式线性映射下, C的内部不是映射成 C的内部便映射成C的外部. 判别方法: 方法1 在分式线性映射下, 如果在圆周C内任取 , 0 一点z 为C的外部. C的内部; , 若 z0的象在C内部 则C的内部就映为 , 若 z0的象在C外部 则C的内部就映

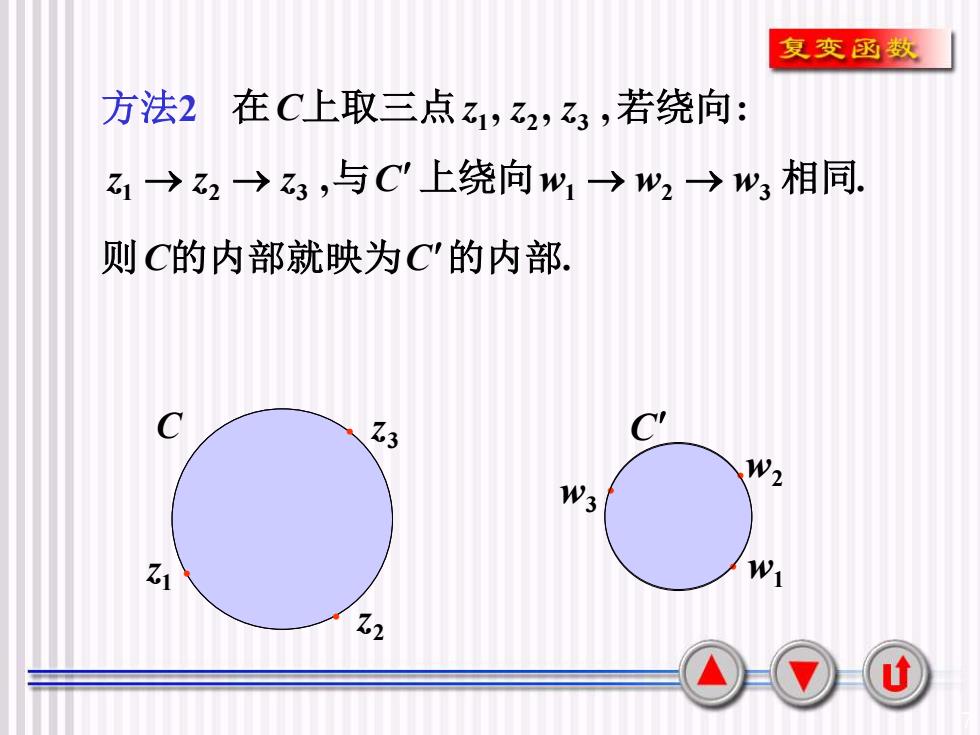
复变函数方法2在C上取三点Z，2，3，若绕向:Z→ Z2 → ,与C"上绕向i→W2 →W 相同则C的内部就映为C'的内部CC'Z.3W2W3W1Z112u

7 方法2 , , , : 在C上取三点z1 z2 z3 若绕向 , . z1 → z2 → z3 与C 上绕向w1 → w2 → w3 相同 w3 . w1 . w2 . C C 1 z . 2 z . . 3 z 则C的内部就映为C的内部

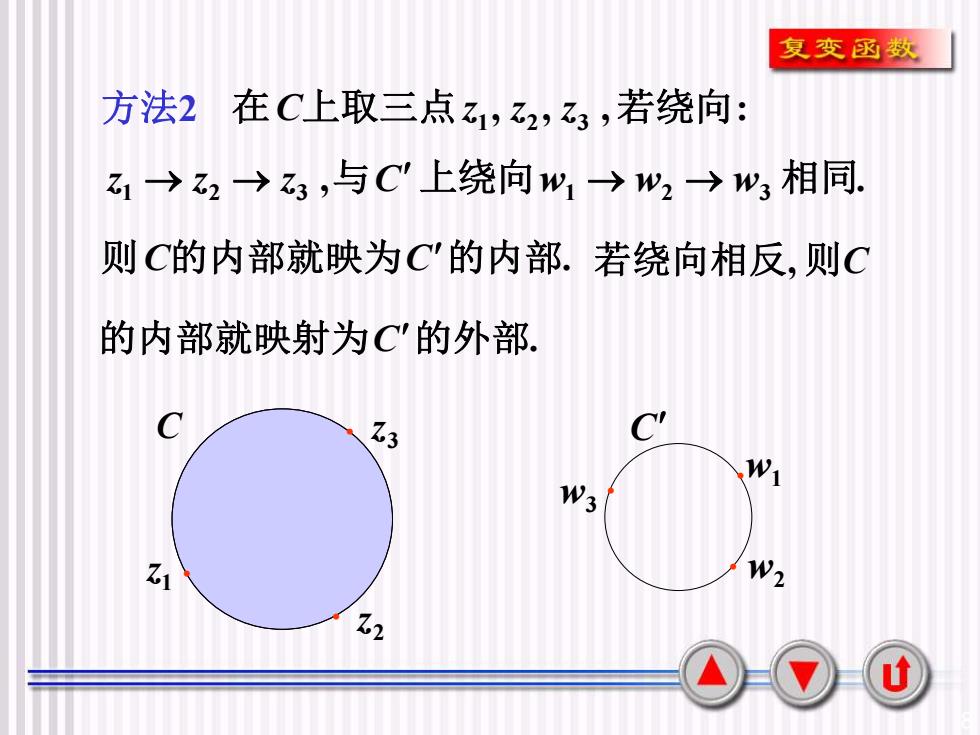
复变函数方法2在C上取三点ZZ2，3，若绕向:Zi→ z2 →3,与C"上绕向wi→W2 →W 相同则C的内部就映为C'的内部．若绕向相反，则C的内部就映射为C'的外部CC'1.3W1W3W2Z1152u

8 C C 若绕向相反, 则C w3 . w2 . w1 . 1 z . 2 z . . 3 z 方法2 , , , : 在C上取三点z1 z2 z3 若绕向 , . z1 → z2 → z3 与C 上绕向w1 → w2 → w3 相同 则C的内部就映为C的内部. 的内部就映射为C的外部

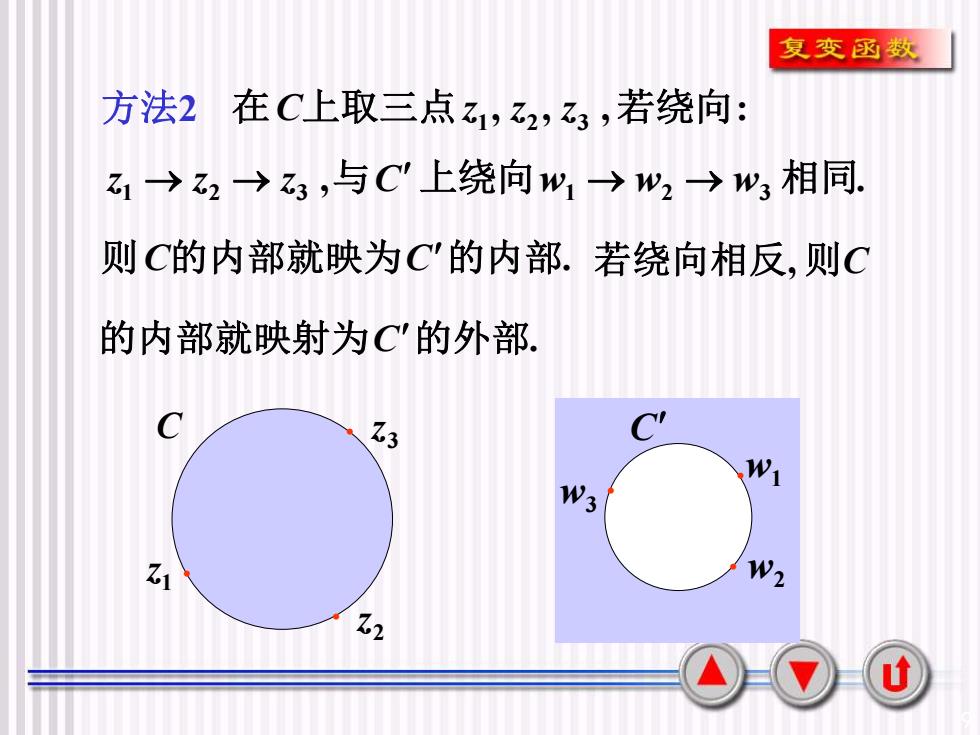
复变函数方法2在C上取三点ZZ2，3，若绕向:Zi→ z2 →3,与C"上绕向wi→W2 →W 相同则C的内部就映为C'的内部．若绕向相反，则C的内部就映射为C'的外部CC1.3W1W3W2Z1152U

9 C C w2 . w1 . w3 . 1 z . 2 z . . 3 z 若绕向相反, 则C 方法2 , , , : 在C上取三点z1 z2 z3 若绕向 , . z1 → z2 → z3 与C 上绕向w1 → w2 → w3 相同 则C的内部就映为C的内部. 的内部就映射为C的外部

复变函数2.分式线性映射对圆弧边界区域的映射：1）当二圆周上没有点映射成无穷远点时这二圆周的弧所围成的区域映射成二圆弧所围成的区域2）当二圆周上有一点映射成无穷远点时这二圆周的弧所围成的区域映射成一圆弧与一直线所围成的区域3）当二圆交点中的一个映射成无穷远点时这二圆周的弧所围成的区域映成角形区域面

10 2.分式线性映射对圆弧边界区域的映射: 这二圆周的弧所围成的区域映射成一圆弧与 一直线所围成的区域. 2) 当二圆周上有一点映射成无穷远点时, 3) 当二圆交点中的一个映射成无穷远点时, 这二圆周的弧所围成的区域映成角形区域. 1) 当二圆周上没有点映射成无穷远点时, 这二圆周的弧所围成的区域映射成二圆弧所 围成的区域