
二、填空 6.lim 3 解 lim 2x+3) lim x 2x+1 1+ 2x 2x3 3 32 1+ lim 2 X→00 =lim 1 1+2x) lim 00
8 二、填空 6. 2 3 lim 2 1 x x x → x + + =_______ 解 2 3 lim 2 1 x x x → x + + 3 1 2 lim 1 1 2 x x x x → + = + 3 1 2 lim 1 1 2 x x x x x → + = + 2 3 3 2 3 2 1 1 2 2 2 3 lim 1 2 1 lim 1 2 x x x x x e e e x → → + = = = +

7.设函数f(x)在x=0点处有f(0)=0,f'(0)=1,那么 lim f(h) h->0 h 解 lim f-lm/0+)-f0=fo)=】 h-→0 h-→0 h 应填1 8.如果函数f(x)在[a,b]上连续,在(a,b)内可导,则在 (a,b)上至少存在一点5,使得f(b)-f(a= 解 此题为lagrange中值定理f(b)-f(a)=f'(5)(b-a) 应填f'()b-a) 9
9 7.设函数 f x( )在x = 0点处有 f (0) 0 = , f (0) 1 = ,那么 0 ( ) lim h f h → h = 解 0 0 ( ) (0 ) (0) lim lim h h f h f h f → → h h + − = = = f (0) 1 应填 1 8.如果函数 f x( )在[ , ] a b 上连续,在( , ) a b 内可导,则在 ( , ) a b 上至少存在一点 ,使得 f b f a ( ) ( ) − = 解 此题为 lagrange 中值定理 f b f a f b a ( ) ( ) ( )( ) − = − 应填 f b a ( )( ) −

9.曲线y=e*+x上点(0,1)处的法线方程 解y=e+1,ylx-0=2 法线方程)-1=x-0.即y=1方 10.由方程-e”+2=0确定的函数y=),求 x 解对方程两端关于x求导 y2+x·2yy-e(y+xy)=0 (2xy-xe)y'=ye-y2 =y=e”- dx 2xy-xe 10
10 9.曲线 x y e x = + 上点(0,1)处的法线方程 解 1 x y e = + , 0 | 2 x y = = 法线方程 1 1 ( 0) 2 y x − = − − ,即 1 1 2 y x = − 10.由方程 2 2 0 xy xy e − + = 确定的函数y y x = ( ),求 dy dx = 解 对方程两端关于x求导 2 2 ( ) 0 xy y x y y e y xy + − + = 2 (2 ) xy xy xy xe y ye y − = − 2 2 xy xy ye y x dy y dx y xe = = − −
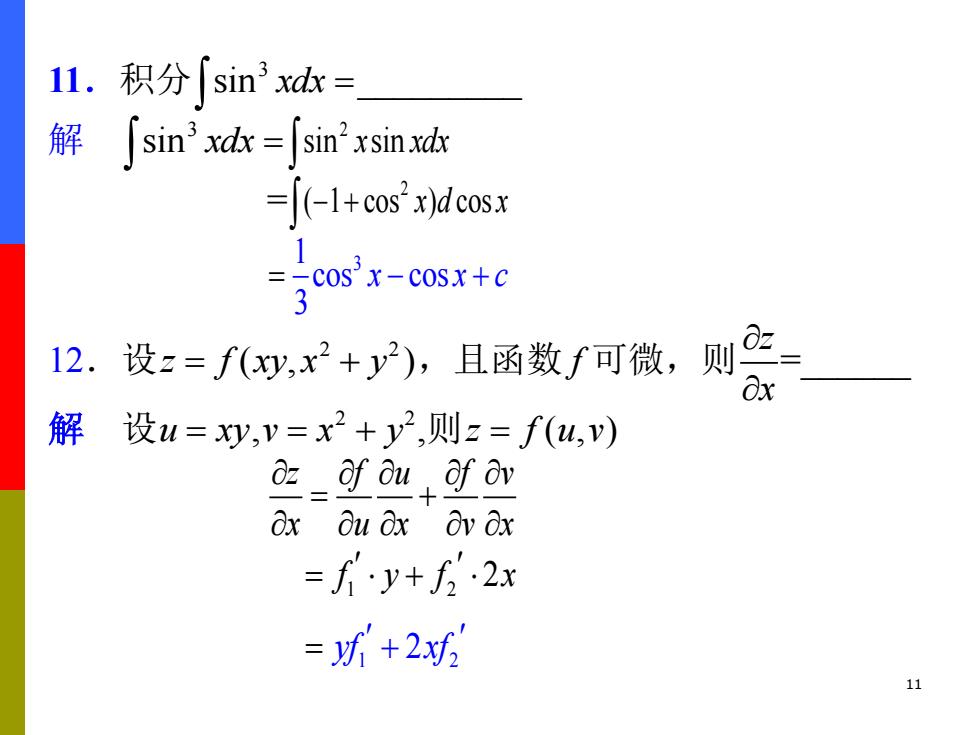
1l.积分sin3xdr= 解∫sin3xd=sin2'xsin xd =[(-1+cosx)dcosx COs3x-C0S 12.设:=f(y,x+),且函数f可微,则 x 解设u=y,v=x2+y2,则z=f(u,v) e of ou ofov Ox Ou Ox Ov Ox =y+2x =才+2x时 11
11 11.积分 3 sin xdx = _________ 解 3 sin xdx = 2 sin sin x xdx = 2 ( 1 cos ) cos − + x d x 1 3 cos cos 3 = x x c − + 12.设 2 2 z f xy x y = + ( , ),且函数 f 可微,则 z x =______ 解 设u xy = , 2 2 v x y = + ,则z f u v = ( , ) z f u f v x u x v x = + 1 1 2 2 2 f y f x2 yf xf = = + +

13.改变二次积分 I=df(x.y+f(x.yre 的积分次序,则1= a6c- 解D: y=x y=x 交点(1,1) 2 y=2-x 0≤x≤1 y=2-x D: x≤y≤2-x 1=「ifx,w 12
12 13.改变二次积分 1 2 2 0 0 1 0 ( , ) ( , ) y y I dy f x y dx dy f x y dx − = + 的积分次序,则I =______ 解 0 1 : 0 y D x y 和 1 2 0 2 y x y − 2 y x y x = = − 交点(1,1) 0 1 : 2 x D x y x − I = 1 2 0 ( , ) x x dx f x y dy − y x = y x = −2 y o 1 x 2