《电路》课程教学资源（PPT课件）第16章 二端口网络

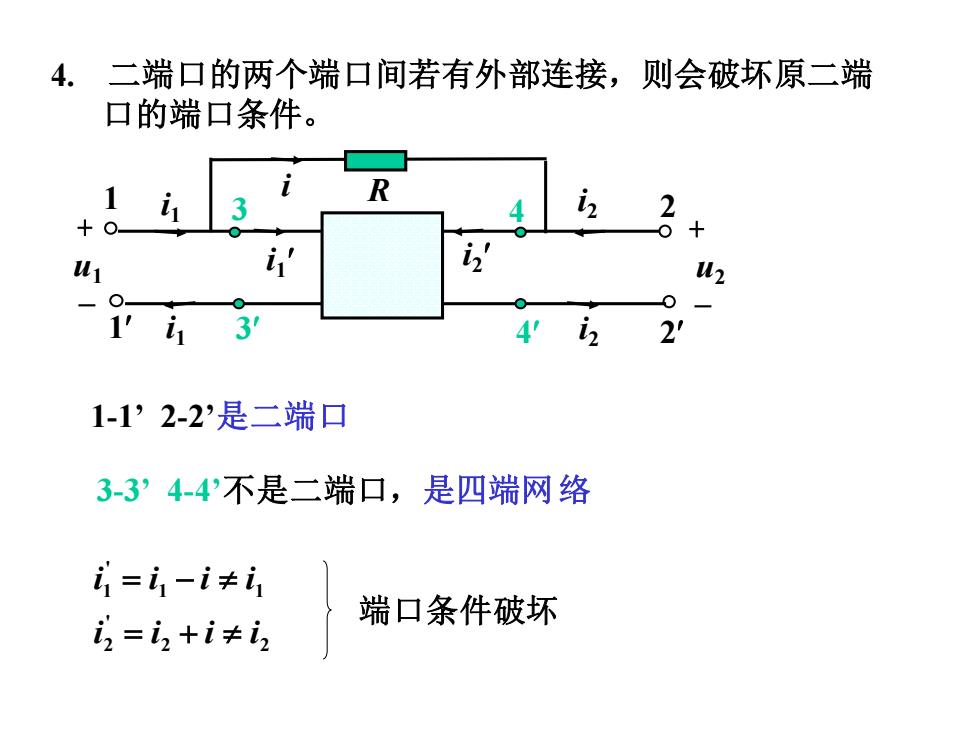
4.二端口的两个端口间若有外部连接，则会破坏原二端 口的端口条件。 1 i 2 1 计 2' u2 1'i 3 4i2 2 1-1?2-2'是二端口 3-3’4-4不是二端口，是四端网络 =i1-i≠i1 i=2+i≠2 端口条件破坏

4. 二端口的两个端口间若有外部连接，则会破坏原二端 口的端口条件。 2 2 ' 2 1 1 ' 1 i i i i i i i i = +  = −  端口条件破坏 i1 i2 i2 i1 u1 + – u2 + – 2 2 1 1 i R i1  i2  3 3 4 4 1-1’ 2-2’是二端口 3-3’ 4-4’不是二端口，是四端网络

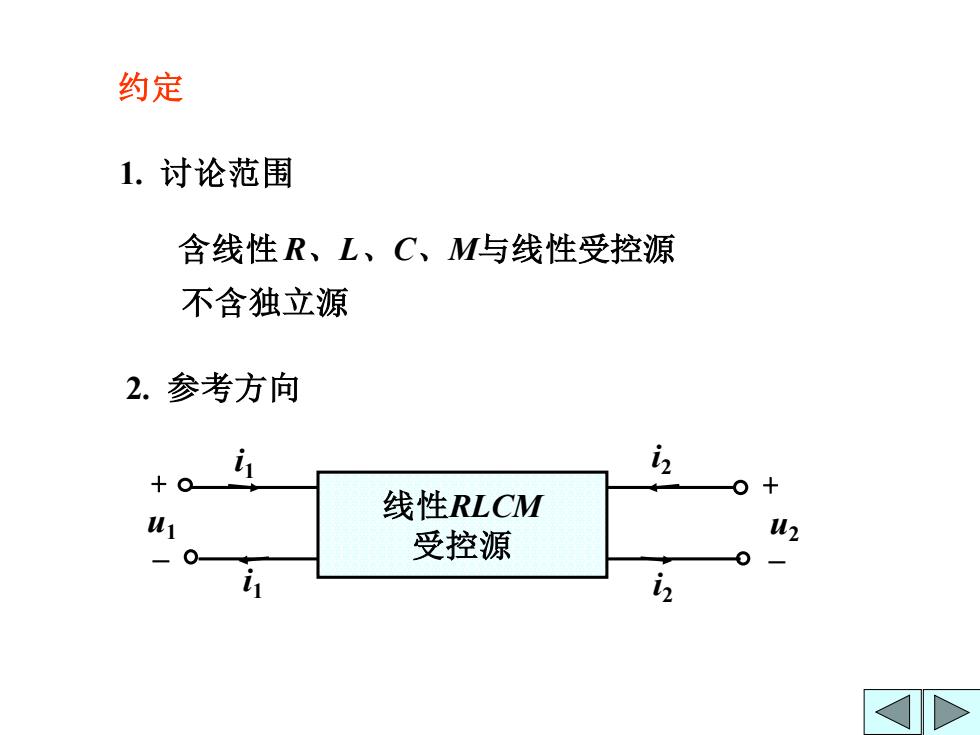
约定 1.讨论范围 含线性R、L、C、M与线性受控源 不含独立源 2.参考方向 2 十 线性RLCM 1 受控源 W2

约定 1. 讨论范围 含线性 R、L、C、M与线性受控源 不含独立源 2. 参考方向 线性RLCM 受控源 i1 i2 i2 i1 u1 + – u2 + –

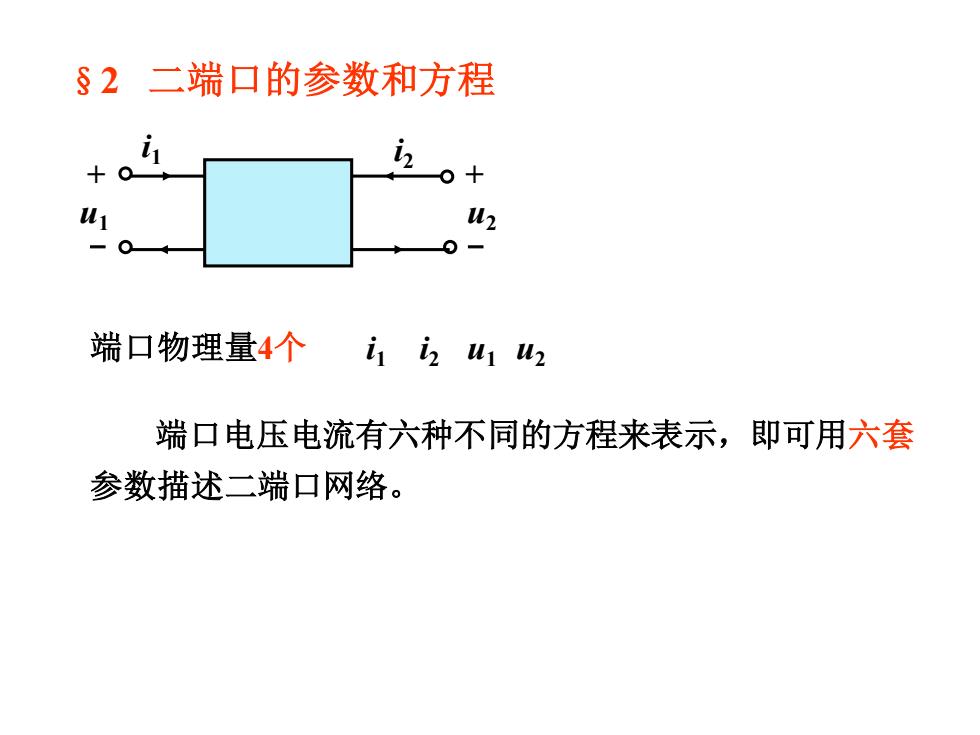
§2二端口的参数和方程 W2 端口物理量4个 ii u uz 端口电压电流有六种不同的方程来表示，即可用六套 参数描述二端口网络

§2 二端口的参数和方程 + - + - i1 i2 u1 u2 端口物理量4个 i1 u1 i2 u2 端口电压电流有六种不同的方程来表示，即可用六套 参数描述二端口网络

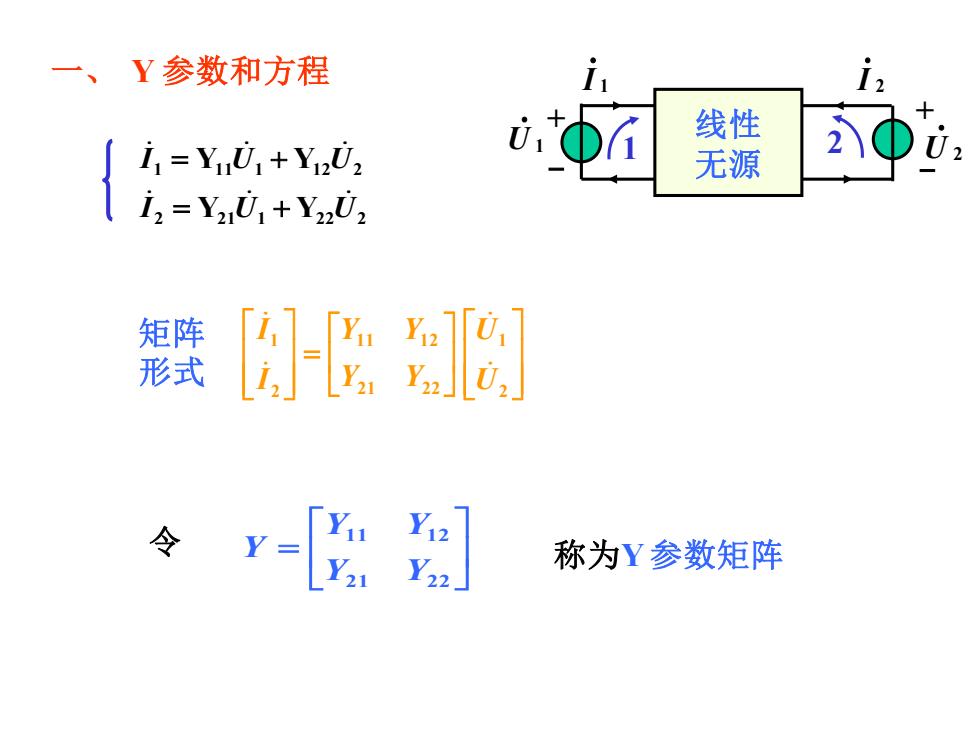
一、Y参数和方程 12 线性 i1=Y01+y0g 无源 2Φ i2=Y201+Y202 矩阵 形式 ] 称为Y参数矩阵

一、 Y 参数和方程 1 2 2 21 1 22 2 1 11 1 12 2 Y Y Y Y I U U I U U       = + = +       = 21 22 11 12 Y Y Y Y 令 Y + - + - 1 • U 1 • I 2 • I 2 • U 线性 无源               =         2 1 21 22 11 12 2 1 U U Y Y Y Y I I     称为Y 参数矩阵 矩阵 形式

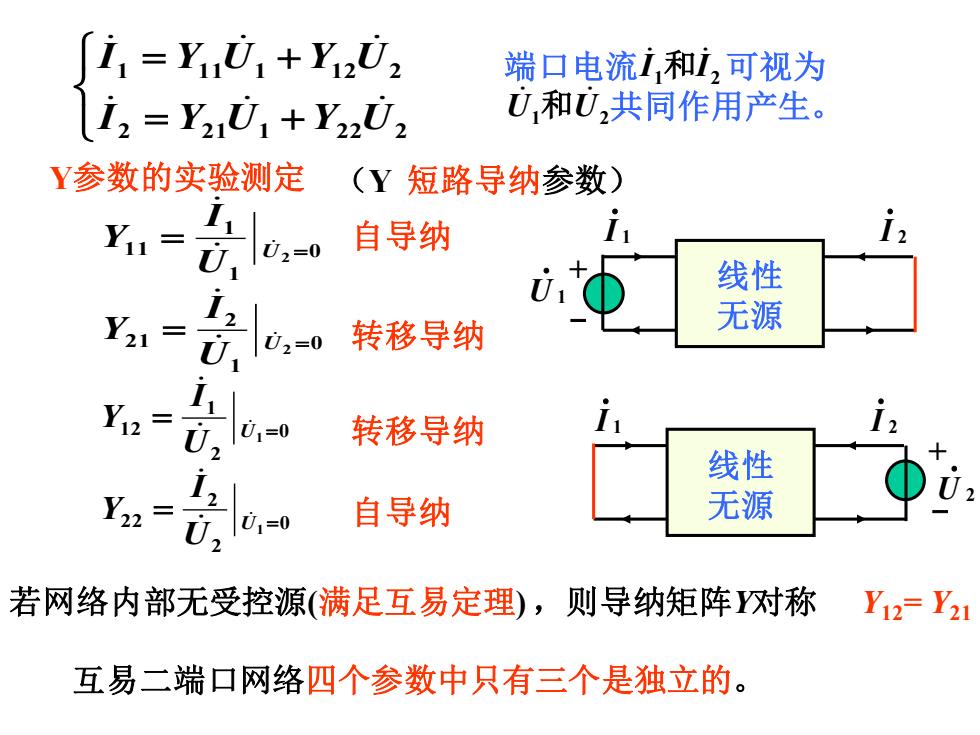
i1=Y01+Y202 端口电流i和i,可视为 i2=Y201+Y2202 0和0，共同作用产生。 Y参数的实验测定 (Y短路导纳参数) Y1= 自导纳 i 01 线性 Y21= 无源 ,0=-0 转移导纳 Y12= i 转移导纳 线性 Y22= 0210=0 自导纳 无源 若网络内部无受控源（满足互易定理），则导纳矩阵对称 互易二端口网络四个参数中只有三个是独立的

    = + = + 2 21 1 22 2 1 11 1 12 2 I Y U Y U I Y U Y U       端口电流 可视为 共同作用产生。 1 2 I I  和 U1 U2  和  Y参数的实验测定 0 2 2 22 1 = = U U I Y    0 1 1 11 2 = = U U I Y    0 1 2 21 2 = = U U I Y    0 2 1 12 1 = = U U I Y    + - 1 • U 1 • I 2 • I 线性 无源 + - 1 • I 2 • I 2 • U 线性 无源 （Y 短路导纳参数） 自导纳 自导纳 转移导纳 转移导纳 若网络内部无受控源(满足互易定理) ，则导纳矩阵Y对称 Y12= Y21 互易二端口网络四个参数中只有三个是独立的