
(7)对称性 a.复数序列的离散时间傅里叶变换的对称性 设xe(n)和xg(n)分别为x(n)的共轭对称和反共轭对称部分 和X(e分别为eo).的共轭对称和反共轭对称部分. 则有以下性质成立 )x(-n)的离散时间傅里叶变换为X(eo) i)x*(-n)的离散时间傅里叶变换为X*(eo) i)Re[x(n)的离散时间傅里叶变换为 Xe)=[X(c刃+X*(em)
(7)对称性 a.复数序列的离散时间傅里叶变换的对称性 设xcs(n)和xca(n)分别为x(n)的共轭对称和反共轭对称部分, 和 分别为 .的共轭对称和反共轭对称部分. 则有以下性质成立: i) x(-n)的离散时间傅里叶变换为 ; ii) x* (-n)的离散时间傅里叶变换为 ; iii) Re [x(n)]的离散时间傅里叶变换为 (e ) j X cs (e ) j X ca (e ) j X (e ) j X − *(e ) j X 1 (e ) [ (e )] *(e ) 2 j j j X X X cs − = +

iv)m(x(n)的离散时间傅里叶变换为 X(e)=X(e】-X*(e) v)x(n)的离散时间傅里叶变换为Re[X(eo】; vi)xea(n)的离散时间傅里叶变换为jlm[X(eo)]; b.实数序列的离散时间傅里叶变换的对称性 设xev(n),xod(n)分别是x(n)偶部和奇部.则有以下性 质成立 i)xev(n)的离散时间傅里叶变换为Re[X(eo)】; i过xo(n)的离散时间傅里叶变换为jm[X(e/o)】;
iv) jIm(x(n))的离散时间傅里叶变换为 v) xcs(n)的离散时间傅里叶变换为 ; vi) xca(n)的离散时间傅里叶变换为 ; 1 (e ) [ (e )] *(e ) 2 j j j X X X ca − = − Re[ (e )] j X Im[ (e )] j j X b.实数序列的离散时间傅里叶变换的对称性 设xev(n), xod(n)分别是x(n)偶部和奇部. 则有以下性 质成立: i) xev (n)的离散时间傅里叶变换为 ; ii) xod(n)的离散时间傅里叶变换为 ; Re[ (e )] j X Im[ (e )] j j X
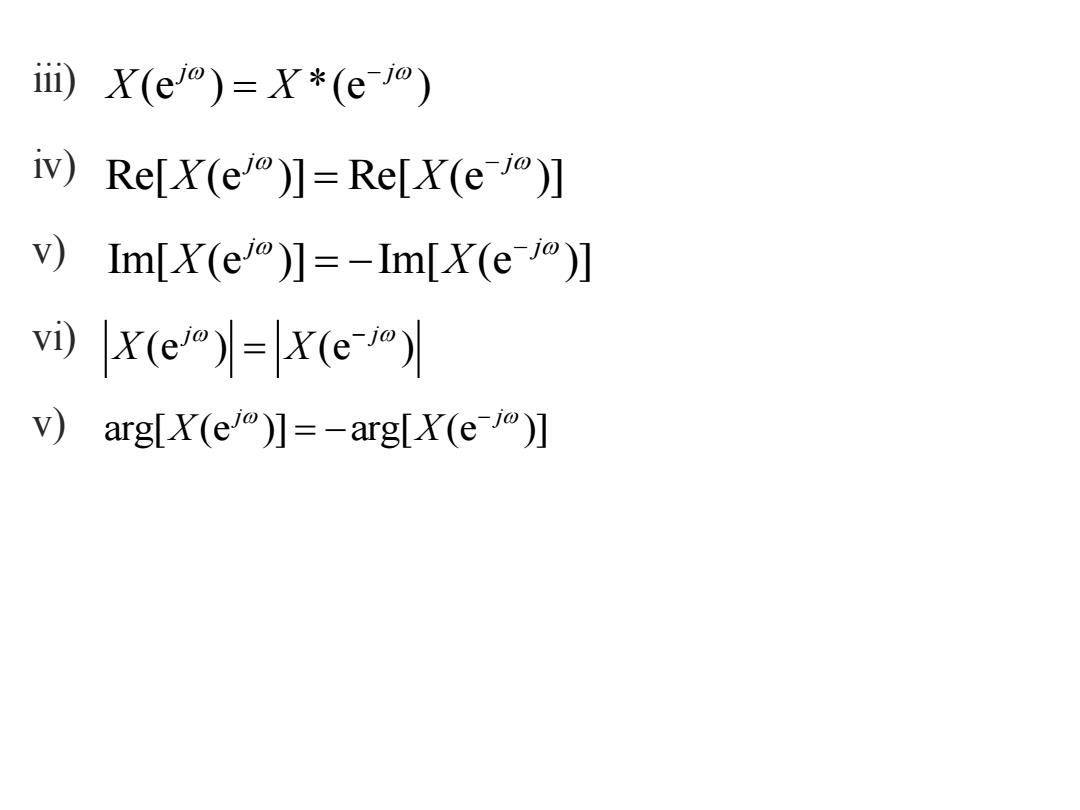
ii)X(ei)=*(e) iv)Re[X(e)]=Re[X(e)] v)Im[X(eo)】=-Im[X(eo)】 vi)X(e)=X(e-) V)arg[X(e)]=-arg[X(e)]
iii) iv) v) vi) v) (e ) *(e ) j j X X − = Re[ (e )] Re[ (e )] j j X X − = Im[ (e )] Im[ (e )] j j X X − = − (e ) (e ) j j X X − = arg[ (e )] arg[ (e )] j j X X − = −

3.Matlab的实现 在Matlab中可以使用内部函数freqz来进行离散时间 傅里叶变换 常用的格式主要有以下两种 H-freqz(num,den,w) 和 H=freqz(num,den,f,FT) 在H=freqz(num,den,w)中,w给出在0到之间的指定频 率集;在H=freqz(num,den,f,FT)中,向量指定了值必 须在0到FT/2之间的频率点,其中FT为采样频率
3. Matlab的实现 在Matlab中可以使用内部函数freqz来进行离散时间 傅里叶变换. 常用的格式主要有以下两种: H=freqz(num,den,w) 和 H=freqz(num,den,f,FT). 在H=freqz(num,den,w)中,w给出在0到之间的指定频 率集;在H=freqz(num,den,f,FT)中,向量f指定了值必 须在0到FT/2之间的频率点,其中FT为采样频率